Решение

 

Знаменатель 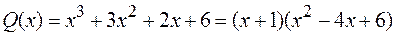, поэтому сумма будет состоять из двух слагаемых: простейшей дроби первого типа, соответствующей линейному множителю 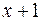, и простейшей дроби третьего типа, соответствующей квадратичному множителю 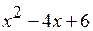. Итак, вид разложения таков:

 

.

 

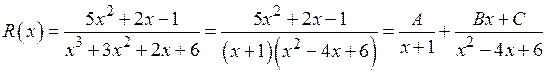Для нахождения 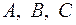приведём правую часть к общему знаменателю:

 

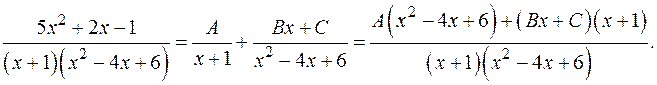
Поскольку дроби в левой и в правой частях этого равенства тождественно равны и имеют одинаковые знаменатели, то тождественно равны и их числители:

 

Составим систему: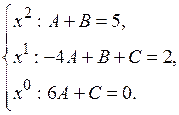

 

Откуда получаем: , , .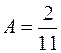

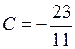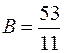Итак, все три неизвестных коэффициента найдены, и получено разложение

 

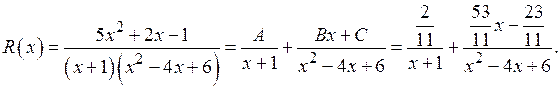
Теперь мы можем представить интеграл от дроби 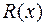в виде:

 

 

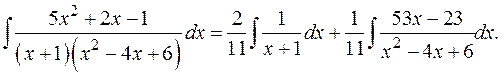
Интеграл в первом слагаемом - табличный: 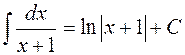. В знаменателе дроби во втором интеграле выделим полный квадрат:

 

 

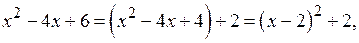
сделаем замену :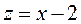

 

 

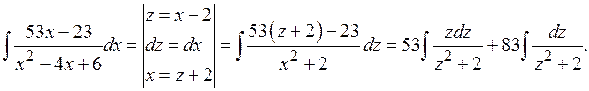
Последний интеграл - табличный:

 

 

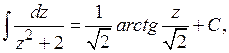
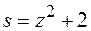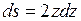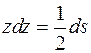а в предыдущем интеграле нужно сделать замену , откуда и , так что этот интеграл приводится к виду .

 

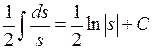Итак,

 

 

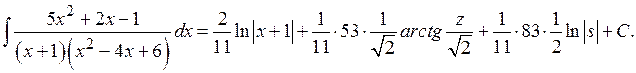
Учитывая, что 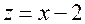и 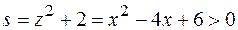, получаем:

 

 

 

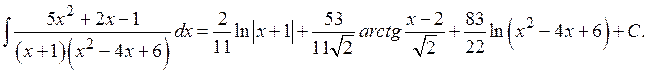
Интегралы, сводящиеся к интегралам от рациональных функций путём замены

 

Рассмотрим интегралы от функций, рациональным образом зависящих от sin x и cos x.

Определение. Будем говорить, что функция 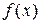рациональным образом зависит от выражения 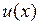, если 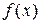можно представить в ви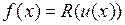де , где 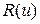- рациональная функция от переменной .

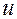Интегралы вида 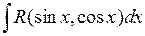, где 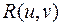- функция, рациональным образом зависящая от u и v, можно привести к интегралу от рациональной функции от одного переменного 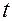, если сделать «универсальную» замену .

 

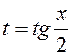При этом:

, ,

 

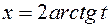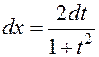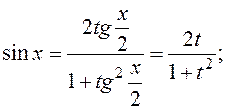
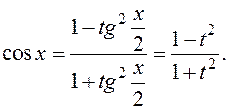
Если имеет место частный случай рациональной зависимости от sin x и cos x, когда обе эти функции входят в выражение лишь в чётных степенях, т. е. подынтегральная функция имеет вид 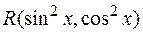, то применять универсальную замену не обязательно: она, как правило, будет приводить к слишком сложным интегралам. В этих случаях гораздо лучше применить другую тригонометрическую замену: .

 

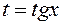Тогда:

, ,

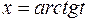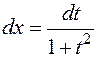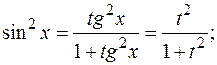
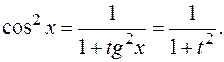
Пример. Вычислить интеграл 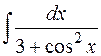.