Решение

.

 

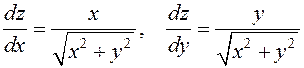Полученные формулы теряют смысл в точке 0 (0; 0).

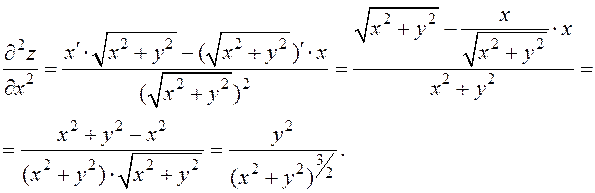
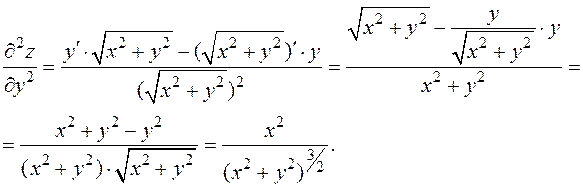
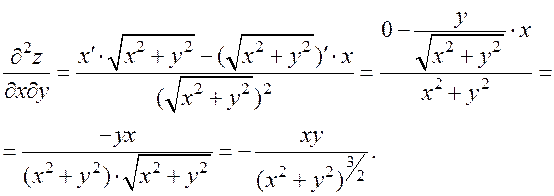
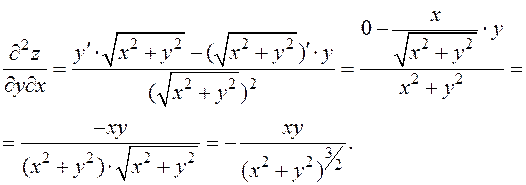
5 Неопределённый интеграл

Пусть на некотором интервале 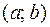задана функция 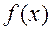. Функция 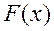называется первообразной для 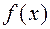на интервале 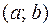, если для всех .

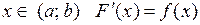Любые две первообразные данной функции 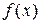отличаются друг от друга на произвольную постоянную. Множество всех первообразных 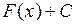, где 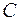- произвольная постоянная, для функции 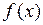на интервале 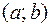называется неопределённым интегралом функции 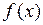. Символически это записывается так:

 

.

 

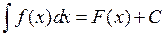Выражение 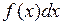называется подынтегральным выражением, функция 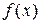- подынтегральной функцией. Вычислить неопределённый интеграл означает найти множество всех первообразных подынтегральной функции.

Основные свойства неопределённого интеграла (правила интегрирования):

· производная от неопределённого интеграла равна подынтегральной функции: ;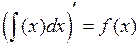

 

· дифференциал от неопределённого интеграла равен подынтегральному выражению: ;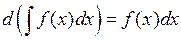

 

· интеграл от дифференциала некоторой функции равен этой функции, сложенной с произвольной постоянной: ;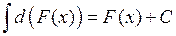

 

· постоянный множитель можно выносить за знак неопределённого интеграла: ;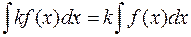

 

· если существуют интегралы 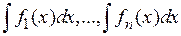, то неопределённый интеграл суммы функций 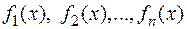равен сумме неопределённых интегралов от этих функций: ;

 

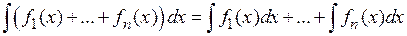· неопределённый интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной: .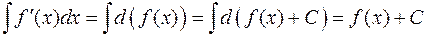

 

Таблица основных неопределённых интегралов

 

1	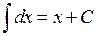12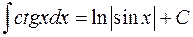
2	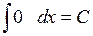13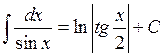
3	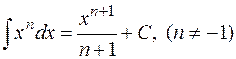14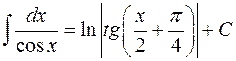
4	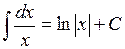15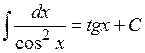
5	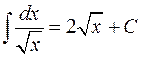16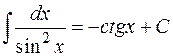
6	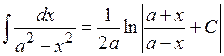17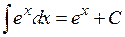
7	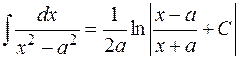18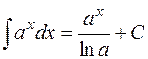
8	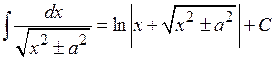19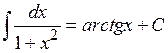
9	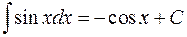20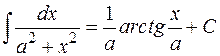
10	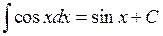21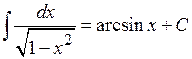
11	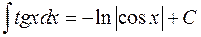22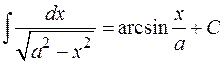