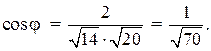Определение скалярного произведения и его свойства
Пусть даны два вектора 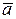 и
и 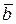 .Тогда их скалярное произведение определяется из равенства
.Тогда их скалярное произведение определяется из равенства 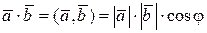 , где j – угол между этими векторами.
, где j – угол между этими векторами.
Если векторы заданы в координатной форме 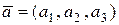 ,
, 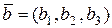 , то их скалярное произведение вычисляется по формуле:
, то их скалярное произведение вычисляется по формуле:
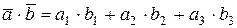 .
.
Скалярное произведение векторов обладает следующими свойствами:
а) 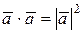 ;
;
б) если 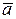 ^
^ 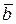 (ортогональные вектора), то
(ортогональные вектора), то 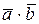 = 0;
= 0;
в) 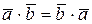 ;
;
г) 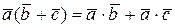 ;
;
д) 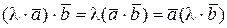 , где λ – любое число.
, где λ – любое число.
Примеры.
а) Найти скалярное произведение векторов 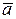 = (2, 1, 1) и
= (2, 1, 1) и 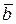 = (2, -5, 1).
= (2, -5, 1).
Из определения имеем 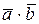 =
= 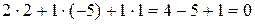 .
.
б) Даны вектор 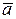 = (m, 3, 4) и вектор
= (m, 3, 4) и вектор 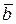 = (4, m, -7). При каких значениях m вектор
= (4, m, -7). При каких значениях m вектор 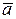 ортогонален вектору
ортогонален вектору 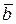 ?
?
Из условий ортогональности имеем: 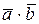 = 4m + 3m -28 = 0,
= 4m + 3m -28 = 0,
7m = 28, m = 4.
в) Найти 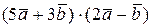 , если
, если 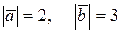 и
и 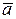 ^
^ 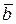 .
.
Из свойств скалярного произведения имеем: 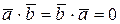 ,
,
так как 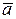 ^
^ 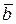 , тогда
, тогда
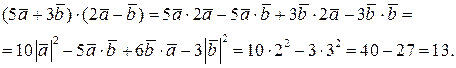
г) Определить угол между векторами 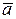 = (1, 2, 3) и
= (1, 2, 3) и 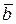 = (0, 4, -2).
= (0, 4, -2).
Так как 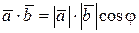 , то
, то 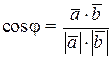 . Из координатного представления векторов находим
. Из координатного представления векторов находим 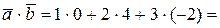 0+8-6=2, по формуле (4.1) имеем
0+8-6=2, по формуле (4.1) имеем 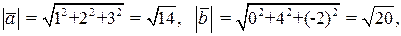 тогда
тогда