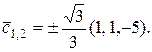Свойства векторного произведения
Отметим следующие свойства векторного произведения:
 а)
а) 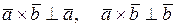 ;
;
б) 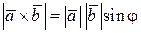 , т.е. модуль векторного произведения равен площади параллелограмма, построенного на векторах
, т.е. модуль векторного произведения равен площади параллелограмма, построенного на векторах 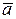 и
и 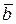 как на сторонах;
как на сторонах;
в) 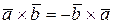 ;
;
г) 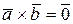 , если либо
, если либо 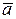 =
= 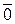 , либо
, либо 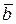 =
= 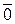 , либо вектора
, либо вектора 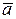 и
и 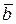 коллинеарны;
коллинеарны;
д) 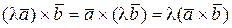 , где λ – любое число;
, где λ – любое число;
е) 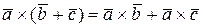 .
.
Приведенные свойства позволяют решать многие задачи геометрии и векторного анализа.
Примеры.
а) Вычислим площадь параллелограмма, построенного на векторах
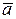 = (3, 6, -2) и
= (3, 6, -2) и 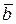 = (-2, 3, 6).
= (-2, 3, 6).
Имеем
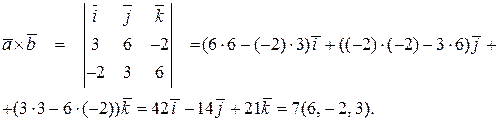
Тогда 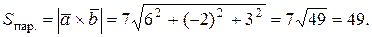
б) Вычислим площадь треугольника с вершинами А(1, 1, 1), В(2, 3, 4), С(4, 3, 2).
На сторонах АВ и АС достроим треугольник до параллелограмма АВСD. Тогда 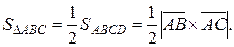 Так как
Так как 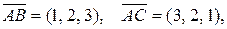 то
то
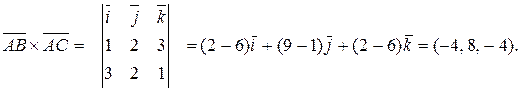
Следовательно, 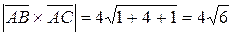 , а
, а 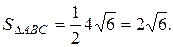
в) Вычислим площадь параллелограмма, построенного на векторах 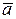 + 3
+ 3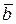 и 3
и 3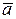 +
+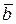 , если
, если 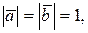 а угол между векторами
а угол между векторами 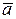 и
и 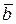 равен p/6.
равен p/6.
Заметим, что 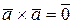 для любого вектора. Следовательно,
для любого вектора. Следовательно, 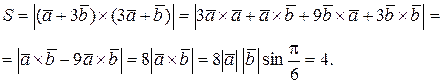
Итак, искомая площадь параллелограмма S=4.
г) Известно, что вектор 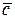 ортогонален векторам
ортогонален векторам 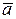 = (3, 2, 1) и
= (3, 2, 1) и 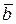 = (2, 3, 1), а |
= (2, 3, 1), а |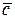 | = 3. Найти вектор
| = 3. Найти вектор 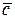 .
.
Так как вектор 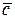 ортогонален векторам
ортогонален векторам 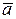 и,
и, 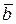 то он коллинеарен вектору
то он коллинеарен вектору 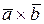 . Имеем
. Имеем
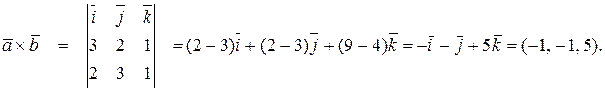
Таким образом, 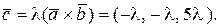 Следовательно,
Следовательно, 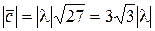 ,
, 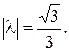 Итак, имеем два вектора, удовлетворяющих условиям задачи:
Итак, имеем два вектора, удовлетворяющих условиям задачи: