Различные виды уравнений прямой на плоскости

Общее уравнение прямой имеет вид

Ах + Ву + С = 0, (8.1)

причем вектор 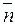= (А, В) ¹ 0. Вектор 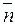является ортогональным к прямой (8.1) и его называют вектором нормали. Если С = 0, то прямая (8.1) проходит через начало координат. Если же С ¹ 0, то после деления уравнения (8.1) на (-С) получаем уравнение прямой в отрезках

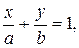(8.2)

где 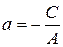; 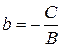, причем (а, 0) и (0, b) – координаты точек пересечения прямой (8.2) с осями координат.

Пример. Составим уравнение прямой, отсекающей на осях координат отрезки а = 0,2, 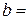-0,1.

Воспользовавшись уравнением (8.2), имеем

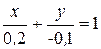или 5х - 10у - 1 = 0.

Если в уравнении (8.1) В = 0, то прямая параллельна оси Оy. Если же В ¹ 0, то уравнение (8.1) можно преобразовать к уравнению прямой с угловым коэффициентом

у = kх + b, (8.3)

где 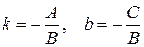, причем 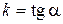, а a – угол, образованный прямой с положительным направлением оси Ох. Свободный член b в (8.3) – ордината точки пересечения прямой с осью Оу.

 

Примеры.

а) Составим уравнение прямой, отсекающей от оси Оу отрезок b= -3 и образующей с этой осью угол b = p/6.

Заметив, что 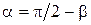, из уравнения (8.3) выводим у = х·tg a - 3 = =х·tg(p/2 -p/6) - 3 = .

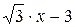б) Представим общее уравнение прямой 12х - 5у - 65 = 0 в виде уравнения в отрезках и уравнения с угловым коэффициентом.

Разрешив общее уравнение прямой относительно у, получим уравнение с угловым коэффициентом: у = 2,4х - 13 (k = -12/-5=2,4, b = -(-65/-5)= -13).

Разделив общее уравнение прямой на 65 и перенеся 1 направо, получим уравнение в отрезках: 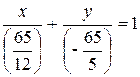(а = 65/12, 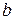= - 13).

Если заданы две прямые:

А₁х + В₁у + С₁ = 0 или у = k₁х + b₁,

А₂х + В₂у + С₂ = 0 или у = k₂х + b₂,

то для острого угла j между ними справедливы формулы:

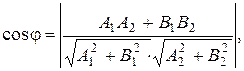(8.4)

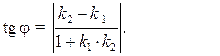(8.5)

Отсюда легко получаем условия параллельности прямых:

А₁/А₂ = В₁/В₂ или k₁ = k₂ (8.6)

и ортогональности прямых:

А₁А₂ + В₁В₂ = 0, или k ₁ = - 1/ k₂. (8.7)

 

Примеры.

а) Определим острый угол между прямыми у = -3х + 7 и у = 2х + 1.

Из формулы (8.5) имеем

tg j = |(2 - (-3))/(1 + (-3)2)| = 5/5 = 1, j = p/4.

б) Покажем, что прямые 4х - 6у + 7 = 0 и 20х - 30у - 11 = 0 параллельны.

Из условий (8.6) имеем 4/20 = (-6)/(-30) = 1/5, т.е. прямые параллельны.

 

в) Покажем, что прямые 3х - 5у + 7 = 0 и 10х + 6у - 3 = 0 ортогональны.

Применяя условие ортогональности (8.7), имеем 3∙10 - 5∙6 = 0 и делаем заключение об ортогональности прямых.

 

Уравнение прямой, проходящей через точку (х₀, у₀) записывается в виде

А(х - х₀) + В(у - у₀) = 0 (8.8)