Прямая и плоскость

Уравнение прямой в пространстве может быть записано как уравнение линии пересечения двух плоскостей в следующем виде:

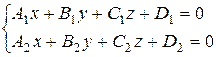. (9.10)

На практике больше применяется каноническое уравнение прямой в пространстве

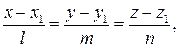(9.11)

где (х₁, у₁, z₁) – точка, через которую эта прямая проходит, а 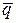= (l, m, n) – вектор, параллельный прямой, называемый направляющим вектором.

Уравнение прямой, проходящей через две точки (х₁, у₁, z₁) и (х₂, у₂, z₂), имеет вид:

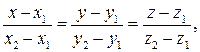(9.12)

 

Пример. Составить уравнение прямой, проходящей через точки 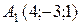и

И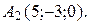спользуя формулу (9.12), получаем

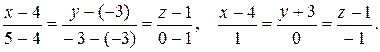
Равенство нулю знаменателя второй дроби означает, что прямая принадлежит плоскости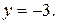

 

Острый угол между двумя прямыми в канонической форме:

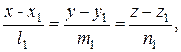
и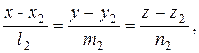

определяется по формуле:

 

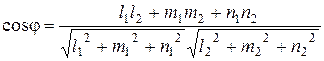. (9.13)

 

Условия параллельности прямых в канонической форме:

 

l₁/l₂ = m₁/m₂ = n₁/n₂. (9.14)

 

Условие ортогональности прямых:

 

l₁l₂ + m₁m₂ + n₁n₂ = 0. (9.15)

 

Примеры.

а) Привести уравнение прямой 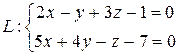к каноническому виду.

Решение.

Выразим из системы х через у и z:

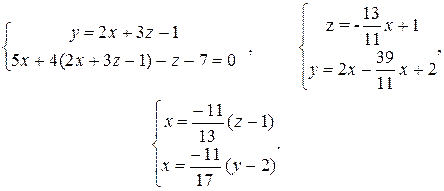
Следовательно,

 

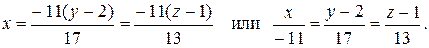
б) Из начала координат опустить перпендикуляр на прямую

(х-2)/2 = (у-1)/3 = (z - 3)/1.

Решение.

Запишем уравнение плоскости, проходящей через начало координат и ортогональной заданной прямой. Так как направляющий вектор заданной прямой 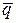= (2, 3, 1) в этом случае ортогонален плоскости, то можно положить 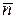= 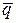и записать уравнение плоскости в виде 2х + 3у + z = 0. Найдем точку пересечения этой плоскости и прямой для чего решим систему:

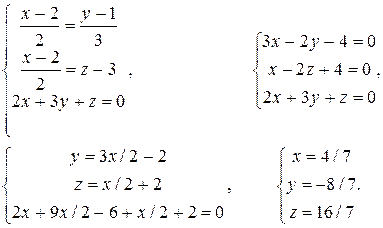
Из уравнения прямой, проходящей через две точки (9.12), получаем искомое уравнение прямой:

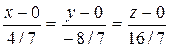или x = y/(-2) = z/4.

в) Через прямую (х + 1)/2 = (у - 1)/(-1) = (z - 2)/3 проведем плоскость, параллельную прямой х/(-1) = (у + 2)/2 = (z - 3)/(-3).

Решение.

Так как вектора 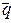₁ = (2, -1, 3) и 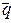₂ = (-1, 2, -3) (направляющие вектора прямых) параллельны плоскости, то их векторное произведение 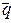₁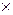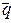₂ ортогонально плоскости, т.е. может быть взято за вектор нормали плоскости.

Итак,

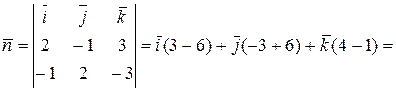3( -1, 1, 1).

 

Прямая (х + 1)/2 = (у - 1)/(-1) = (z - 2)/3 лежит в плоскости. Следовательно, и точка (-1, 1, 2), через которую она проходит, находится там же. Таким образом, искомое уравнение плоскости можно записать в виде

-(х + 1) + (у - 1) + (z -2 ) = 0 или х - у - z + 4 =0.