Задачи для самостоятельного решения

Задача 1) Написать уравнение прямой, проходящей через точку А(2, 0, -3) параллельно:

1) вектору 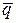=(2, -3, 5);

2) прямой (х - 1)/5 = (у + 2)/2 = (z + 1)/(-1);

3) прямой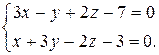

 

Задача 2) Задана плоскость x + y - z + 1 = 0 и прямая (x - 1)/0 = y/2 = (z + 1)/1.

Требуется:

1) вычислить угол между ними;

2) написать уравнение плоскости, проходящей через данную прямую перпендикулярно к данной плоскости.

Задача 3) Доказать, что прямые

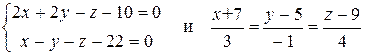
параллельны, и найти расстояние между ними.

 

Задача 4) Найти проекцию точки С(3, -4, -2) на плоскость, проходящую через параллельные прямые

 

10. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ

 

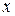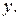Кривая второго порядка на плоскости – это линия, определяемая уравнением 2-й степени от переменных и Мы рассмотрим три основные линии второго порядка.

Эллипс – множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная (равная 2а).

Если фокусы располагаются в точках 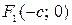и , то эллипс имеет каноническое уравнение:

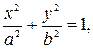где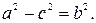

Величина 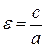называется эксцентриситетом эллипса, а прямые – его директрисами.

Гипербола – множество точек, таких, что модуль разности расстояния каждой из которых от двух данных точек (фокусов) есть постоянная величина 2а. Если фокусы располагаются в точках 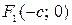и , то каноническое уравнение гиперболы:

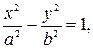где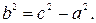

Величина 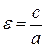называется эксцентриситетом гиперболы, а прямые 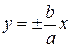– её асимптотами.

Парабола – это множество точек, равноудалённых от данной точки (фокуса 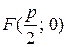) и от данной прямой – директрисы. Её каноническое уравнение имеет вид:

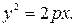
Уравнение директрисы параболы имеет вид: .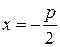

Примеры.

а) Написать каноническое уравнение эллипса, если 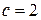и расстояние между директрисами равно .

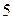Решение.

Расстояние между директрисами эллипса равно 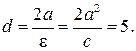Отсюда 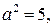следовательно, 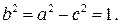В итоге, каноническое уравнение эллипса имеет вид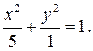

б) Написать каноническое уравнение гиперболы, если ,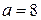

 

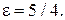
Решение.

Эксцентриситет гиперболы равен 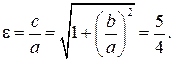Следовательно, 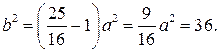Поэтому каноническое уравнение гиперболы имеет вид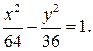

в) Написать уравнение параболы с вершиной в начале координат, если фокус параболы находится в точке .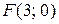

 

Решение.

Фокус параболы находится в точке с координатами 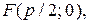поэтому 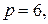и уравнение параболы имеет вид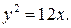

 

11. ВВЕДЕНИЕ В АНАЛИЗ