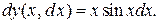Производная функции. Основные определения и обозначения
Назовем разность 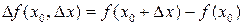 – приращением функции
– приращением функции 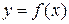 в точке
в точке 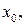 соответствующим приращению аргумента
соответствующим приращению аргумента 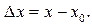 Производной функции
Производной функции 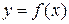 в точке
в точке 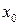 называется предел
называется предел
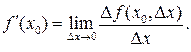
Производная функции 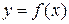 , рассматриваемая на множестве тех точек, где она существует, сама является функцией. Процесс нахождения производной называют также дифференцированием. Для нахождения производных нужно пользоваться таблицей производных основных элементарных функций и правилами дифференцирования функций.
, рассматриваемая на множестве тех точек, где она существует, сама является функцией. Процесс нахождения производной называют также дифференцированием. Для нахождения производных нужно пользоваться таблицей производных основных элементарных функций и правилами дифференцирования функций.
Таблица производных основных элементарных функций.
1. 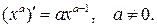
2. 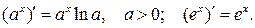
3. 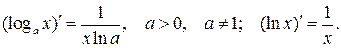
4. 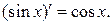
5. 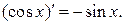
6. 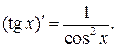
7. 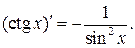
8. 
9. 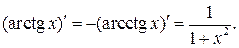
Правила дифференцирования функций
1. Пусть C-константа и функции 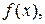
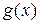 имеют производную в точке
имеют производную в точке 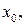 тогда:
тогда:
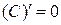 ;
; 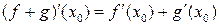 ;
; 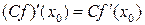 ;
;
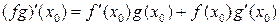 ;
; 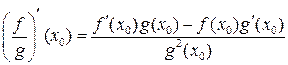 .
.
2. Пусть функция 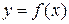 имеет производную в точке
имеет производную в точке 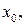 а функция
а функция 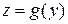 имеет производную в точке
имеет производную в точке 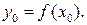 Тогда сложная функция
Тогда сложная функция 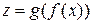 в точке
в точке 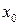 имеет производную, равную
имеет производную, равную 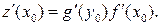
Второе свойство называется правилом дифференцирования сложной функции.
Пример. Найти производную функции 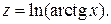
Полагая 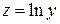 и
и 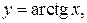 имеем
имеем 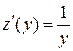 и
и 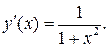 Отсюда, согласно правилу дифференцирования сложной функции, получаем
Отсюда, согласно правилу дифференцирования сложной функции, получаем 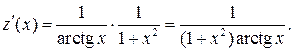
Логарифмической производной функции 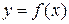 называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е. 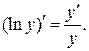 Применение предварительного логарифмирования часто упрощает вычисление производной.
Применение предварительного логарифмирования часто упрощает вычисление производной.
Примеры.
а) Найти производную функции 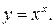
Логарифмируя, получим 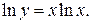 Отсюда находим производные левой и правой части
Отсюда находим производные левой и правой части 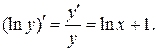 Следовательно,
Следовательно, 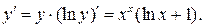
б) Найти производную функции 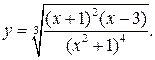
Логарифмируя, получим 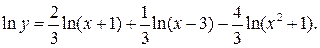 Находя производные левой и правой части, получаем
Находя производные левой и правой части, получаем
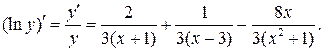
Следовательно, 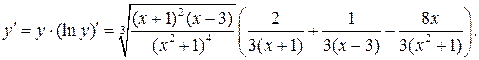
Пусть на интервале 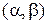 заданы две функции
заданы две функции 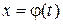 и
и 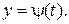 Если при этом функция
Если при этом функция 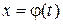 на интервале
на интервале 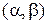 имеет обратную
имеет обратную 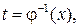 то определена новая функция
то определена новая функция 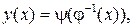 называемая функцией, заданной параметрически соотношениями
называемая функцией, заданной параметрически соотношениями 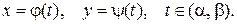 Переменная
Переменная 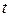 называется в этом случае параметром. Производная функции, заданной параметрически, находится по формуле
называется в этом случае параметром. Производная функции, заданной параметрически, находится по формуле 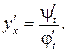
Пример. Найти 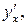 если функция задана параметрически
если функция задана параметрически
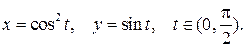
Поскольку 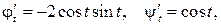 то получаем
то получаем 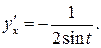
Функция неявно задана на интервале 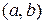 уравнением
уравнением 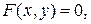 если для всех
если для всех 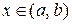 выполнено равенство
выполнено равенство 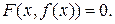 Для вычисления производной функции
Для вычисления производной функции 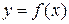 нужно равенство
нужно равенство 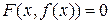 продифференцировать по
продифференцировать по 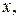 а затем полученное уравнение разрешить относительно
а затем полученное уравнение разрешить относительно 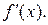
Пример.
Найти производную функции 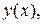 заданной неявно
заданной неявно 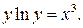
Дифференцируем по 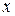 это равенство и получаем
это равенство и получаем 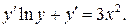 Отсюда
Отсюда 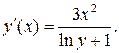
Производной 2-го порядка от функции 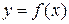 называется производная от ее первой производной, т.е.
называется производная от ее первой производной, т.е. 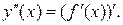 Для производной 2-го порядка используется также обозначение
Для производной 2-го порядка используется также обозначение 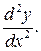
Пример. Найти 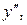 если
если 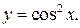
Имеем 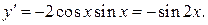 Следовательно,
Следовательно, 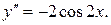
Если приращение функции 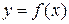 в точке
в точке 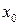 можно представить в виде
можно представить в виде 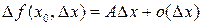 при
при 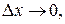 где
где 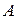 – некоторое число, то линейная часть этого приращения
– некоторое число, то линейная часть этого приращения 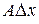 называется дифференциалом этой функции в точке
называется дифференциалом этой функции в точке 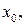 соответствующим приращению
соответствующим приращению 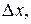 и обозначается символом
и обозначается символом 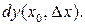
Для того чтобы функция 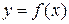 была дифференцируемой в точке
была дифференцируемой в точке 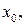 необходимо и достаточно, чтобы существовала производная
необходимо и достаточно, чтобы существовала производная 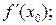 при этом справедливо равенство
при этом справедливо равенство 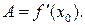 Поэтому выражение для дифференциала имеет вид
Поэтому выражение для дифференциала имеет вид 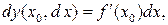 где принято обозначение
где принято обозначение 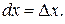
Пример. Найти дифференциал функции 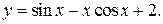
Находим производную этой функции 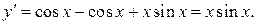 Следовательно,
Следовательно,