Возрастание и убывание функций. Экстремум
Функция 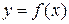 называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале 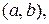 если из неравенства
если из неравенства 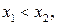 где
где 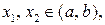 следует неравенство
следует неравенство 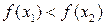 (соответственно
(соответственно 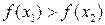 ).
).
Если функция 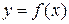 дифференцируема на интервале
дифференцируема на интервале 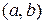 и
и 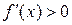 при всех
при всех 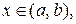 то функция
то функция 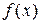 возрастает на
возрастает на 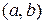 ; если же
; если же 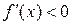 при всех
при всех 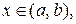 то функция
то функция 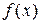 убывает на
убывает на 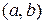 .
.
В простейших случаях область определения функции можно разбить на конечное число интервалов монотонности. Каждый из интервалов монотонности ограничен критическими точками, в которых производная функции обращается в нуль или не существует.
Если существует такой интервал 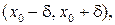 что для всякой точки
что для всякой точки 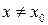 из этого интервала выполняется неравенство
из этого интервала выполняется неравенство 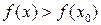 (или
(или 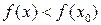 ), то точка
), то точка 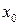 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 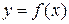 , а число
, а число 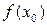 – минимумом (максимумом) этой функции. Точки минимума и максимума функции называются ее точками экстремума.
– минимумом (максимумом) этой функции. Точки минимума и максимума функции называются ее точками экстремума.
Необходимое условие экстремума функции. Если 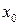 – точка экстремума функции
– точка экстремума функции 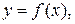 то
то 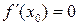 или
или 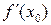 не существует, т.е.
не существует, т.е. 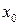 – критическая точка этой функции.
– критическая точка этой функции.
Достаточные условия экстремума непрерывной функции.
1) Если функция 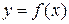 дифференцируема в некоторой окрестности критической точки
дифференцируема в некоторой окрестности критической точки 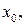 за исключением, быть может, самой этой точки, и ее производная слева от этой точки положительная, а справа – отрицательная, то точка
за исключением, быть может, самой этой точки, и ее производная слева от этой точки положительная, а справа – отрицательная, то точка 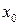 является точкой максимума; если производная слева от точки
является точкой максимума; если производная слева от точки 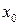 отрицательная, а справа – положительная, то точка
отрицательная, а справа – положительная, то точка 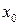 является точкой минимума; если производная слева и справа от точки
является точкой минимума; если производная слева и справа от точки 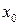 имеет одинаковый знак, то в этой точке функция экстремума не имеет.
имеет одинаковый знак, то в этой точке функция экстремума не имеет.
2) Если в критической точке 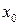 вторая производная отлична от нулю, то в этой точке функция
вторая производная отлична от нулю, то в этой точке функция 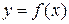 имеет максимум при
имеет максимум при 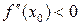 и минимум при
и минимум при 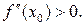
Пример.
Найти интервалы монотонности и точки экстремума для функции 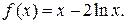
Решение.
Находим производную 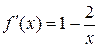 и приравниваем ее нулю. Решая получившееся уравнение
и приравниваем ее нулю. Решая получившееся уравнение 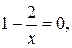 получаем
получаем 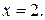 Следовательно, критическими точками (с учетом тех точек, где производная не определена) являются:
Следовательно, критическими точками (с учетом тех точек, где производная не определена) являются: 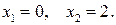 Область определения
Область определения 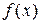 разбивается на два интервала монотонности:
разбивается на два интервала монотонности: 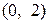 и
и 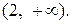 Так как
Так как 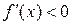 при
при 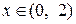 и
и 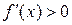 при
при 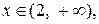 то
то 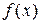 убывает на интервале
убывает на интервале 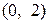 и возрастает на интервале
и возрастает на интервале 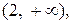 а в точке
а в точке 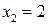 достигает минимума
достигает минимума