Экстремумы функций нескольких переменных

 

Говорят, что функция 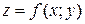имеет локальный максимум в точке 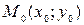, т.е. при 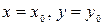, если 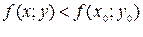для всех точек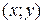, достаточно близких к точке 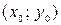(т.е. лежащих в некоторой её окрестности) и отличных от неё.

Говорят, что функция 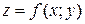имеет локальный минимум в точке 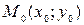, т.е. при 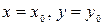, если 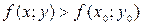для всех точек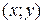, достаточно близких к точке 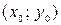и отличных от неё.

(Слово «локальный» мы, далее, будем опускать).
Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция 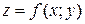достигает экстремума при 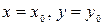, то каждая частная производная первого порядка от 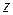или обращается в ноль при этих значениях аргументов, или не существует.

Точки, в которых частная производная первого порядка обращается в ноль, называются стационарными.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку 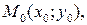функция 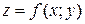имеет непрерывные частные производные до второго порядка включительно. Пусть, кроме того, точка 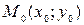является стационарной точкой функции 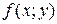, т.е.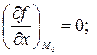 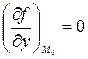. Обозначим 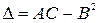, где

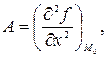
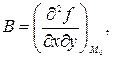
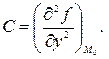
Тогда при :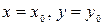
1) 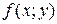имеет максимум, есл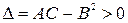и и .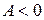
2) 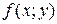имеет минимум, есл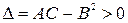и и .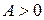
3) 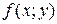не имеет ни минимума, ни максимума, если .
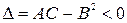4) если 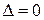, то экстремум может быть, а может и не быть (требуется дополнительное исследование).

 

Пример. Найти экстремум функции .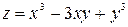

Решение. Сначала найдем частные производные:

, .

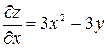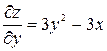Стационарные точки найдем из системы уравнений:

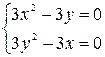
Система имеет два решения: 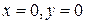и 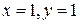. Значит, имеются две стационарные точки – это 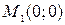и .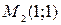

Находим производные второго порядка данной функции:

,

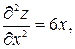
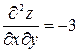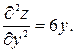
В точке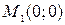имеем 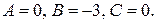Так как 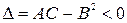, то в этой точке экстремума нет.

В точке 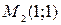имеем 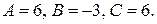Так как, 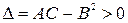и А>0, то функция в этой точке имеет минимум.