Производные высших порядков.
Производной 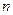 -го порядка (или
-го порядка (или 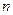 -ой производной) называется производная от
-ой производной) называется производная от  порядка:
порядка:
 (2.23)
(2.23)
Производные порядка выше первого называются производными высших порядков. Обозначения производных высших порядков функции 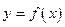
 .
.
2.1.Найти производные функций:
а) ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) 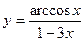 .
.
Решение.
а) Используем правило (2.2), (2.1), и формулу (2.9) получим
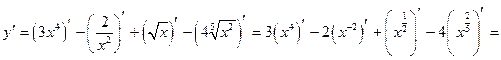
 .
.
б) Используя формулы (2.2), (2.9), (2.10), (2.7) имеем

в) Используя правило (2.3), и формулы (2.11), (2.13) получаем

г) При вычислении производной функции, равной произведению более двух функций, ее представляют в виде произведения двух функций  :
:
Дважды используем правило (2.3):

Используем формулы (2.10), (2.15), (2.9):

д) Используется правило (2.4), (2.2), (2.1) и формулы (2.19) (2.7), (2.8). Имеем
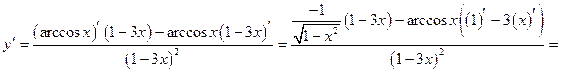
 . ►
. ►
2.2.Найти производные функций:
а)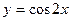 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Решение.
В этих примерах рассматриваются производные сложных функций.
а) Введем функцию  , тогда
, тогда  .
.
Используем правило (2.5), и формулу (2.14):.
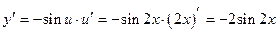 .
.
б) Введем функцию  , тогда
, тогда  .
.
Используем правило (2.5), и формулы (2.14), (2,9):

в) Введем функцию  , тогда
, тогда  . Используем правило (2.5) и формулы (2.10), (2.17):
. Используем правило (2.5) и формулы (2.10), (2.17):
 .
.
г) Правило вычисления производной сложной функции используется дважды. Введем функцию  , тогда
, тогда 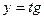 и используем формулы (2.5) и (2.16):
и используем формулы (2.5) и (2.16):

Пусть  , тогда
, тогда 
Используем правило (2.5), и формулу (2.12):

Тогда 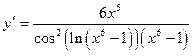 ►
►
2.3.Вывести формулу вычисления производной функции 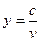 , где
, где  ,
,
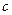 - постоянная.
- постоянная.
Использовать полученную формулу при вычислении производной функции  .
.
Решение.
1) Можно использовать формулу (2.4) или (2.5). Согласно формуле (2.9) имеем  .
.
Тогда  .Поэтому
.Поэтому
 (2.24)
(2.24)
2) Введем  , тогда
, тогда 
Используем формулу (2.24) и (2.18): 
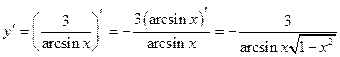 ►
►
2.4.Найти производные функций
а) ;
;
б) 
Решение.
а) Основание и показатель степени являются функциями от аргумента 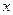 .
.
Используем метод логарифмического дифференцирования:
 ,
,
 ,
,
 ;
;
 ;
;

б) Производная вычисляется аналогично примеру. а) Проведем метод логарифмического дифференцирования:
 ;
;
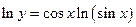 ;
;
 ;
;
 ;
;
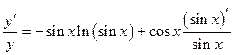 ;
;
 ;
;
 . ►
. ►
2.5.Найти производную функции
 в точке
в точке  .
.
Решение.
В заданной функции 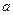 является постоянной, а
является постоянной, а 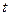 - переменной. Используем формулу
- переменной. Используем формулу
 , тогда
, тогда 
Имеем  . ►
. ►
2.6.Найти производную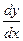 неявной функции
неявной функции 
Решение.
Возьмем производную от левой и правой частей тождества, учитывая, что 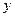 зависит от переменной
зависит от переменной 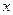 :
:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Выразим 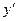 из уравнения:
из уравнения:
 . ►
. ►
2.7.Найти производные 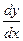 ,
,  функции, заданной параметрически.
функции, заданной параметрически.

Решение.
Найдем производные от заданных функций по переменной 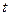 ;
;
 ,
,
Используем формулу (2.22) для нахождения производной функции 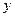 по
по 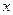 :
:
 :
: 
Найденная производная является функцией от переменной 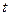 . Получили новую функцию, заданную параметрически:
. Получили новую функцию, заданную параметрически:

Используем формулу (2.22). Тогда
 :
:
Найдем производную от функции 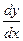 по переменной
по переменной 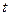 :
:
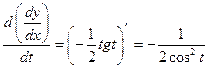
Имеем
 . ►
. ►
2.8.Найти производную 3-го порядка функции 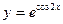
Решение. Последовательно дифференцируем функцию:
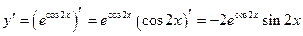 ;
;

 ;
;



 . ►
. ►
2.9.Найти производную 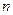 - го порядка функции
- го порядка функции  .
.
Решение. Для некоторых функций можно вывести формулу 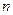 -ой производной.
-ой производной.
Проводится последовательное дифференцирование функции:
 ;
;
 ;
;

 . ►
. ►
Найти производные функций:
2.10. 
2.11. 
2.12. 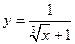
2.13. 
2.14. 
2.15. 
2.16. 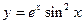
2.17. 
2.18. 
2.19. 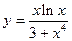
2.20. 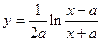
2.21. 
2.22. 
2.23. 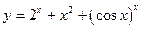
2.24. 
Найти производные  от неявной функции;
от неявной функции;
2.25. 
2.26. 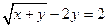
2.27. 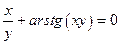
2.28. 
Найти производные функций заданных параметрически:
2.29. 2.30.
2.30.
2.31. 2.32.
2.32.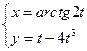
Найти производные второго порядка функций:
2.34.  2.35.
2.35. 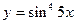
2.36.  2.37.
2.37. 
Найти производные 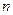 -го порядка функций:
-го порядка функций:
2.38.  2.39.
2.39. 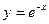
2.40.Показать, что функция удовлетворяет уравнению
удовлетворяет уравнению 