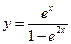ДИФФЕРЕНЦИАЛ ФУНКЦИИ
1. Если функция 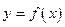 имеет производную
имеет производную  в точке
в точке 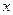 , то полное приращение функции
, то полное приращение функции  можно записать в виде
можно записать в виде  , где
, где 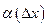 - бесконечно малая функция при
- бесконечно малая функция при 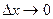 , т.е.
, т.е.  .
.
Дифференциалом первого порядка функции 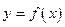 называется главная,линейная относительно
называется главная,линейная относительно 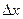 часть приращения функции, равная произведению производной на приращение независимой переменной:
часть приращения функции, равная произведению производной на приращение независимой переменной:
 (1.1)
(1.1)
Если 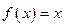 , то
, то  , поэтому для дифференциал обычно записывается в виде
, поэтому для дифференциал обычно записывается в виде
 (1.2)
(1.2)
При достаточно малых приращениях аргумента 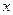 дифференциал функции мало отличается от полного приращения:
дифференциал функции мало отличается от полного приращения:  .
.
Это свойство используется при вычислении приближенных значений функций:
 (1.3)
(1.3)
2. Дифференциалом 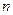 -го порядка
-го порядка 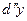 называется дифференциал от дифференциала
называется дифференциал от дифференциала
 -го порядка.
-го порядка.
 (1.4)
(1.4)
Имеет место соотношение
 (1.5)
(1.5)
1.1. Найти дифференциал функции 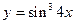 .
.
Решение. Найдем производную функции

Обратимся к формуле (1.2)
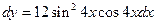 . ►
. ►
1.2. Вычислить приближенно 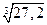
Решение. Требуется найти приближенное значение функции 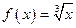 в точке
в точке 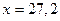 . Ближайшей точкой к значению,
. Ближайшей точкой к значению, 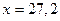 , в которой значение функции вычисляется легко, является
, в которой значение функции вычисляется легко, является  .
.
Найдем приращение независимой переменной;
 .
.
Найдем значение функции и ее производной в точке  :
:

Используем формулу (1.3).
 ,
,
 ,
,
 . ►
. ►
1.3. Найти дифференциал третьего порядка от функции 
Решение. Используем формулу (1.5)
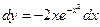 ;
;
 ;
;

 . ►
. ►
Вычислить приближенные значения:
1.4. ; 1.5.
; 1.5.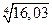 ; 1.6.
; 1.6. .
.
Найти дифференциалы функций:
1.7.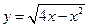 ;
;
1.8.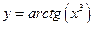 .
.
Найти дифференциалы второго порядка функций:
1.9.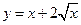 ; 1.10.
; 1.10.