Свойства смешанного произведения.

1. Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на трех исходящих из одной точки векторах. Смешанное произведение больше нуля, если тройка правая, и отрицательная, если она левая.

Доказательство: Отложим вектора , , 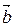из одной точки. Возможны две ситуации:

a) Тройка , , 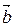– правая; б) Тройка , , 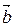– левая.

 

 

 

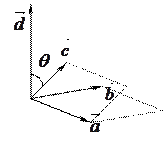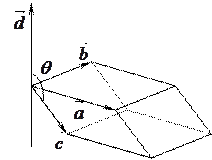Пусть .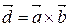

Тогда

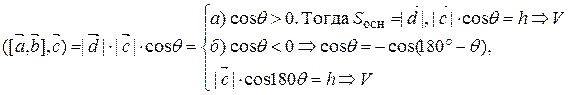
2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

Доказательство. Если один из векторов нулевой, то свойство очевидно.

Пусть , , 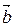¹ 0.

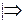Пусть , , 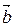– компланарны. Тогда ^.

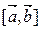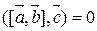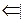Пусть 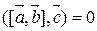Þ л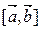ибо ^, либо .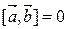

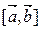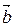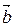В первом случае это означает, что вектор ^ векторам , , Þ , , – компланарны. Во втором случае – ||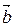Þ и 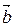– линейно зависимы Þ , , 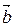– компланарны.

3. Смешанное произведение не зависит от группировки сомножителей, т.е. .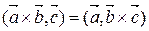

Доказательство. Тройк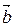и , , и 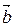, , ориентированы одинаково, значит знак смешанного произведения одинаковый. Модуль так же одинаковый в силу свойства 1.

Обозначение. Смешанное произведение векторов , , 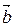обозначается .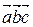

4. .

Следует из свойства циклической перестановки ориентированных векторов.

5. , .

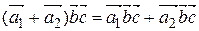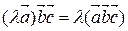Следует из свойств скалярного произведения.