Свойства алгоритмов
Рассмотренные примеры показывают, что выполнение алгоритма разбивается на последовательность законченных действий-шагов. Каждое действие должно быть закончено исполнителем прежде, чем он приступит к исполнению следующего действия. Это свойство алгоритма называется дискретностью.
Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой.
Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было известно, какую команду надо выполнить следующей. Это свойство алгоритма называется точностью.
Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может ее исполнить в строгом соответствии с ее назначением. Это свойство называется понятностью (для данного исполнителя).
- Да пойми же, гайками прикрепляется рельса к шпалам!
- Это мы понимаем...
А. Чехов «Злоумышленник»
Будучи понятным, алгоритм не должен все же содержать предписаний, смысл которых может восприниматься неоднозначно. Это означает, что одно и то же предписание после исполнения должно давать один и тот же результат.
В данном случае речь фактически идет о том, что запись алгоритма должна быть настолько четкой, настолько полной и продуманной в деталях, чтобы у исполнителя никогда не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места, для произвола исполнителя.
Отмеченное свойство называется свойством определенности, или детерминированности.
Замечание. Часто под свойством детерминированности алгоритма понимается одновременное выполнение свойств точности и понятности.
Важным свойством алгоритма является свойство результативности. Смысл этого свойства состоит в том, что при точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет.
Считается, что алгоритм наиболее интересен, если он, кроме того, обладает свойством массовости, т.е. пригодности для решения любой задачи из некоторого класса задач. Это свойство не следует понимать как возможность решить много задач. Свойство массовости предполагает, что заданный алгоритм позволяет решить любую задачу из определенного класса, причем этот класс может состоять и только из одной задачи.
Проиллюстрируем свойства алгоритма на примере алгоритма Евклида.
Массовость алгоритма Евклида заключается в том, что его можно применить к любой паре натуральных чисел. Результативность его состоит в том, что он определяет процесс, приводящий для любой пары натуральных чисел к получению их наибольшего делителя. Понятность алгоритма заключается в том, что исполнитель умеет выполнять действия, определяемые командами алгоритма. Детерминированность алгоритма вытекает из того, что каждая команда выполняется исполнителем однозначно. Точность алгоритма обеспечивается тем, что, во-первых, исполнителю известно, с чего начинать выполнение алгоритма (с команды номер 1), и, во-вторых, каждая команда снабжена указанием, какую команду выполнять следующей.
Рис.2.1. Непонятное предписание
Очевидно, не каждое правило, приводящее к решению задачи, является алгоритмом. Разберем с этих позиций несколько таких правил.
Пример 2.1. Проведение перпендикуляра к прямой MN в заданной точке A [2].
I. Отложить в обе стороны от точки A на прямой MN циркулем отрезки равной длины с концами B и C,
2. Увеличить раствор циркуля до радиуса, в полтора-два раза большего длины отрезков AB в AC.
3. Провести указанным раствором циркуля последовательно с центрами B и C дуги окружностей так, чтобы они охватили точку A и образовали две точки пересечения друг с другом D и E.
4. Взять линейку и приложить ее к точкам D и E и соединить их отрезком. При правильном построении отрезок пройдет через точку А и будет искомым перпендикуляром

Рис. 2.2. Проведение перпендикуляра к прямой
в заданной точке
Указанное правило, очевидно, рассчитано на исполнителя-человека. Применяя его, человек, разумеется, построит искомый перпендикуляр. Но, тем не менее, это правило алгоритмом не является.
Прежде всего, оно не обладает свойством детерминированности. Так, в пункте 1 требуется от исполнителя сделать выбор отрезка произвольной длины (для построения точек B и C надо провести окружность произвольного радиуса r с центром в точке A). В пункте 2 требуется сделать выбор отрезка в полтора-два раза большего длины отрезков AB и AC. В пункте 3 надо провести дуги, которые также однозначно не определяются их описанием. Человек-исполнитель, применяющий данное правило, к одним и тем же исходным данным (прямой MN и точке A) повторно, получит несовпадающие промежуточные результаты. Это противоречит требованию детерминированности алгоритма.
Попробуем переформулировать это правило, чтобы оно стало алгоритмом. Для этого следует во всех предписаниях избавить исполнителя от проблемы выбора.
Для этого мы вместо выбора произвольного радиуса будем указывать в каждом случае конкретный. Однако, этим неопределенность команд полностью не снимается. В инструкциях 1 и 2, кроме проведения окружностей, требуется находить точки пересечения и как-то их обозначать. Разберем возникающие при этом проблемы.
В команде 2 требуется присвоить имена точкам пересечения прямой MN и окружности  . Здесь можно договориться обозначать точки, например, так, чтобы векторы
. Здесь можно договориться обозначать точки, например, так, чтобы векторы  и
и  были сонаправлены.
были сонаправлены.
В команде 3 требуется обозначить точки пересечения окружностей и
и . Договоримся, например, обозначать через D ту из двух точек пересечения, которая находится левее, если смотреть из центра B в направлении центра C.
. Договоримся, например, обозначать через D ту из двух точек пересечения, которая находится левее, если смотреть из центра B в направлении центра C.
Кроме того, вместо дуг окружностей в пункте 3, мы будем проводить окружности, ибо тем самым снимается неопределенность инструкции «провести дугу, охватывающую точку».
С учетом сказанного искомый алгоритм может выглядеть следующим образом.
Пример 2.2. Алгоритм проведения перпендикуляра к прямой MN в заданной точке A ( ).
).
1. Провести окружность  радиуса 1 с центром в точке A.
радиуса 1 с центром в точке A.
2. Обозначить точки пересечения окружности  с прямой MN через B и C так, чтобы
с прямой MN через B и C так, чтобы  .
.
3. Последовательно провести окружности и
и радиуса 2 с центром соответственно в точках B и C.
радиуса 2 с центром соответственно в точках B и C.
4. Обозначить точки пересечения окружностей  и
и через D и E так, чтобы обход многоугольника BDCE (последовательно от B через D и C к E) совершался по часовой стрелке.
через D и E так, чтобы обход многоугольника BDCE (последовательно от B через D и C к E) совершался по часовой стрелке.
5. Провести прямую DE. Прямая DE - искомый перпендикуляр.
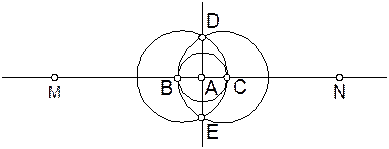
Рис.2.3. Проведение перпендикуляра к прямой
в заданной точке
В школьном учебнике [1] приведен алгоритм нахождения середины отрезка при помощи циркуля и линейки. В нем использован другой прием избавления от неопределенности инструкций при геометрических построениях.
Замечание. Подробное обсуждение вопросов, связанных с алгоритмами построения циркулем и линейкой, проводится в [3]. Всем, изучающим информатику, полезно познакомиться с этой интересной книгой.