АКСИОМАТИЧЕСКИАЯ ТЕОРИЯ

Вопросы к экзамену

2. Булевы функции. Табличное задание булевых функций. Задание булевых функций целыми числами. Графическое представление булевых функций.… 3. Алгебра булевых функций. Принцип двойственности. 4. Приложение алгебры высказываний к логико-математической практике. Прямая, обратная и противоположная теоремы.…

Образцы экзаменационных билетов

Билет № 1 1. Дедуктивный характер математики. Предмет математической логики, ее роль в… 2. Формальные теории (как строится формальная теория). Вывод, доказательство, теорема, метатеорема. Исчисление…

Приложение 1

 

Е. П. Емельченков, В. Е. Емельченков

 

 

АКСИОМАТИЧЕСКИЕ ТЕОРИИ

Рассматривается аксиоматический метод построения математических теорий. Обсуждаются свойства непротиворечивости и полноты аксиоматических теорий. …   Греки превратили математику в логическую систему, в которой от исходных предположений с помощью логического вывода,…

Понятие аксиоматической теории

На уроке геометрии. Учитель: «Для чего мы изучаем аксиомы?» Ученик: «Чтобы их не доказывать».   Аксиоматический метод не является достижением только двадцатого столетия. В начале двадцатого века, благодаря главным…

Как возникают аксиоматические теории

Первый путь состоит в том, что та или иная математическая теория, достигнув достаточно высокого уровня развития, принимает характер аксиоматической… Второй путь возникновения аксиоматических теорий состоит в том, что…  

Примеры аксиоматических теорий

Приведем два примера аксиоматических теорий.

Пример 3.1. Теория аффинных плоскостей. Первичными понятиями этой теории являются точка и прямая, характеризующие принадлежность объектов аксиоматической теории некоторым множествам (множеству точек и множеству прямых). Третьим первичным понятием теории является инцидентность, характеризующее определенное соответствие между точками и прямыми. Если точка A связана соответствием инцидентности с прямой a, то говорят, что точка A инцидентна прямой a, и пишут A I a.

Все свойства прямых, точек и отношения инцидентности описываются тремя аксиомами.

A1. Существуют три точки не инцидентные одной прямой.

A2. Любые две различные точки инцидентны единственной прямой.

Прежде чем сформулировать третью аксиому, введем определение.

Определение D1. Две прямые l и m, не имеющие ни одной общей точки или полностью совпадающие, называются параллельными (обозначение: l m).

A3 (аксиома параллельных). Для любой точки A и прямой l существует единственная прямая m такая, что A I m и m l.

Поразительно, что такая бедная аксиоматика приводит к содержательной теории.

Пример 3.2. Теория эквивалентности. В качестве простого примера аксиоматической теории рассмотрим теорию, описывающую отношение эквивалентности. Эта теория имеет дело с одним типом объектов, множество которых будем обозначать буквой X. Для этих объектов не вводится специальное название (но можно было бы, конечно, назвать их как угодно). Объекты связаны единственным бинарным отношением a. При этом требуется выполнение трех аксиом B1-B3.

B1. Отношение a транзитивно, то есть для любых трех объектов из a a b и b a c следует a a c.

B2. Отношение a симметрично, то есть для любых двух объектов из a a b следует b a a.

B3. Отношение a рефлексивно, то есть для любого объекта 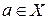выполняется условие a a a.

Для читателей, не знакомых с бинарными отношениями, ниже приводятся необходимые определения и примеры. Более подробное изложение вопросов, связанных с бинарными отношениями, можно найти в одной из предыдущих лекций [1].

Определение 3.1. Бинарным отношением на множестве X называется любая совокупность упорядоченных пар (x, y), где x, y Î X.

Например, пусть X = {a, b, c, d, e}. Тогда множество кортежей a = {(a, b), (a, c), (b, d), (c, e), (e, e), (e, b)} является отношением на множестве X.

Обычно отношения задаются не перечислением элементов множества a, а путем указания свойства пар (x, y), принадлежащих этому множеству. Например, отношение a = {(4, 4), (3, 3), (2, 2), (4, 2)} на множестве X = {4, 3, 2} можно определить как свойство «делится» на этом подмножестве целых чисел.

Хорошо известными примерами отношений из школьного курса математики являются:

· на множестве целых чисел Z отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;

· на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;

· на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

Факт принадлежности кортежа (x, y) отношению a, часто обозначают с помощью так называемой инфиксной формы записи: x a y. Типичными примерами таких записей из курса математики являются: x > y, a = b, 8 4, m l, a b и т. п.

Широко распространен способ представления отношений, основанный на использовании ориентированных графов. При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x, y) отношения a дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y. Граф бинарного отношения a из приведенного выше примера изображен на рисунке 3.1.

 

Рис. 3.1. Граф бинарного отношения
на множестве {a, b, c, d, e}

 

Очевидно, что произвольные бинарные отношения изучать в общем плане не особенно интересно, о них можно сказать очень мало. Однако, если отношения удовлетворяют некоторым дополнительным условиям, относительно них можно делать более содержательные утверждения. В аксиомах были перечислены три свойства бинарных отношений: транзитивность, рефлексивность и симметричность.

Примерами транзитивных отношений служат:

· отношение «делится» на множестве действительных чисел;

· отношение «больше» на множестве действительных чисел;

· отношение «старше» на множестве людей игрушек;

· отношение «иметь одинаковый цвет» на множестве детских игрушек;

· отношение «быть потомком» на множестве людей.

Отношение «быть похожим» на множестве людей не обладает свойством транзитивности.

Примерами симметричных отношений являются:

· отношение перпендикулярности на множестве прямых;

· отношение касания на множестве окружностей;

· отношение «быть похожим» на множестве людей;

· отношение «иметь одинаковый пол» на множестве животных.

Отношение «x брат y» на множестве всех людей не является симметричным. В то же время отношение «x брат y» на множестве мужчин симметричным является.

В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x.

В графе рефлексивного отношения в каждой вершине графа обязательно имеется петля.

Определение 3.2. Бинарное отношение a на X называется антирефлексивным, если ни для одного 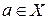не выполняется условие a a a.

Определение 3.3. Бинарное отношение a на множестве X называется антисимметричным, если для любых различных элементов условия a a b и b a a не выполняются одновременно.

Например, отношение «делится» на множестве натуральных чисел является антисимметричным, так как из следует, что a = b. Однако на множестве целых чисел отношение «делится» антисимметричным не является, так как , но -2 ¹ 2.

Отношения «выше», «тяжелее», «старше» антисимметричны на множестве людей. Отношение «быть сестрой» на множестве всех людей антисимметричным не является.

В графе антисимметричного отношения две различные вершины могут быть соединены не более чем одной дугой.

Определение 3.4. Бинарное отношение a на множестве X называется связным, если для любых двух различных элементов a и b имеет место a a b, либо b a a.

Примером связного отношения является отношение «больше» на множестве действительных чисел. Отношение «делится» на множестве целых чисел связным не является.

 

Интерпретации и модели аксиоматической теории

Определение 4.1. Приписывание значений первичным понятиям аксиоматической теории называется интерпретацией теории. Если некоторая совокупность… Другими словами, интерпретация теории - просто отображение f, областью… Так для теории эквивалентности ее моделями служат:

Свойства аксиоматических теорий

Непротиворечивость является важнейшим требованием, предъявляемым к аксиоматическим теориям.   Пословицы противоречат одна другой. В этом собственно и заключается народная мудрость. С.Е. Лец

Упражнения

5.2. Докажите непротиворечивость аксиоматической теории с одним бинарным отношением a, удовлетворяющим аксиомам симметричности и… 5.3. Докажите непротиворечивость аксиоматической теории строгого линейного… 5.4*. Докажите непротиворечивость аксиоматической теории проективных плоскостей. Эта теория имеет дело с двумя типами…

Упражнения

5.5. Докажите неполноту аксиоматической теории порядка.

5.6. Докажите неполноту аксиоматической теории с одним бинарным отношением a, удовлетворяющим аксиомам симметричности и антисимметричности.

5.8. Исследуйте на полноту аксиоматическую теорию AT (пример 4.1).

5.7^*. Докажите неполноту аксиоматической теории проективных плоскостей.

 

Формулировка аксиоматической теории

Как уже говорилось, неформальная теория T включает в себя некоторый список T0 неопределяемых терминов, список T1 определяемых терминов, список P0… Изучение теории T может привести нас к обнаружению самых разнообразных и… Для многих общеизвестных аксиоматических теорий имеются различные формулировки. Различные формулировки какой-либо…

Упражнения

2. Проверьте на независимость системы аксиом а) теории порядка (упражнение 5.1); б) теории строгого линейного порядка (упражнение 5.3);

Литература

1. Е. П. Емельченков, В. Е. Емельченков. Бинарные отношения. Отношение эквивалентности. // Математическая морфология. Смоленск: Изд-во СГМА, 1997. Том 2, вып. 2. С. 3-20.

2. Столл Роберт Р. Множества. Логика. Аксиоматические теории. М.: Просвещение, 1968.

 

 

Приложение 2

 

ã Е. П. Емельченков, В. Е. Емельченков

 

 

ВЫЧИСЛИМОСТЬ. ВВЕДЕНИЕ В ТЕОРИЮ АЛГОРИТМОВ

 

Рассматриваются основные понятия теории алгоритмов. Исследуется неразрешимость многих проблем важных для теоретического программирования.

 

Понятие алгоритма является не только центральным понятием теории алгоритмов, не только одним из главных понятий математики вообще, но одним из главных понятий современной науки. Более того, сегодня, с наступлением эры информатики, алгоритмы становятся одним из важнейших факторов цивилизации.

Успенский В.А., Семенов А.Л. С. 10

Введение

Точное понятие «алгоритм» было выработано лишь в тридцатых годах XX века. До этого математики довольствовались интуитивным понятием алгоритма. Это объясняется тем, что до середины XIX века математика имела дело в основном с числами и вычислениями. Понятие алгоритма отождествлялось с понятием метода вычислений. Все многообразие вычислений комбинировалось из четко определенных операций арифметики, тригонометрии и анализа. Поэтому понятие метода вычисления считалось интуитивно ясным и не нуждалось в специальных исследованиях.

Новые более жесткие требования к строгости стимулировались в основном математикой нечисловых объектов во второй половине XIX века. Одним из решающих обстоятельств, приведших к пересмотру оснований математики, явилось создание Кантором теории множеств.

Опыт парадоксов теории множеств научил математику крайне осторожно обращаться с бесконечностью и даже о бесконечности рассуждать с помощью финитных методов. Существо финитного подхода заключается в том, что он допускает только конечные комплексы действий над конечным числом объектов. Выяснение того, какие объекты и действия над ними следует считать точно определенными, какими свойствами и возможностями обладают комбинации элементарных действий, что можно и чего нельзя сделать с их помощью – все это стало предметом теории алгоритмов. Главным внутриматематическим приложением теории алгоритмов явились доказательства невозможности алгоритмического решения некоторых математических проблем. Такие доказательства неосуществимы без точного понятия алгоритма (для доказательства несуществования алгоритма решения того или иного класса задач, надо точно знать несуществование чего требуется доказать).

 

Интуитивное понятие алгоритма

a) подготовиться к уроку по математике; b) приготовить раствор для проявления фотопленки; c) избавиться от лишнего веса.

Упражнения

1.2. Опишите правила перехода улицы для случаев: а) перекресток регулируемый; б) перекресток нерегулируемый (т.е. без светофора).

Свойства алгоритмов

Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой. Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было… Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может ее исполнить в…

Уточнение понятия алгоритма

Людвиг Витгенштейн (Эпиграф, предпосланный изложению языка программирования АЛГОЛ-60.) Точное математическое определение понятия «алгоритм» было выработано лишь в… Попытки дать строгое математическое определение алгоритма, согласующееся с интуитивным представлением об алгоритме,…

Упражнение

3.1. Покажите, что вычисление по алгоритму из примера 6 с начальной конфигурацией 6, 7, 0, 0, 0, ... никогда не остановится.

Для удобства обозначим через P(a₁, a₂, ..., a_n) вычисление по алгоритму P с начальной конфигурацией a₁, a₂, ..., a_n, 0, 0, .... Если вычислительный процесс заканчивается с результатом b, будем писать P(a₁, a₂, ..., a_n) = b.

Определение 3.1. Пусть f - функция от n неотрицательных целых переменных со значениями во множестве Z₀ неотрицательных целых чисел (функция ). Функция f называется вычислимой на МНР (или МНР–вычислимой), если существует такой алгоритм P, что

1) вычисление P(a₁, a₂, ..., a_n) останавливается тогда и только тогда, когда (a₁, a₂, ..., a_n) принадлежит области определения f;

2) если (a₁, a₂, ..., a_n) принадлежит области определения f; то в заключительной конфигурации в регистре R₁ находится целое число b такое, что f(a₁, a₂, ..., a_n) = b.

С этого момента под термином вычислимое будем подразумевать МНР–вычислимое.

Рассмотрим теперь несколько простых примеров вычислимых функций.

Пример 3.2. Докажите МНР-вычислимость функции x + y.

Решение. Получим x + y, прибавляя y раз 1 к числу x. Начальной конфигурацией алгоритма служит x, y, 0, 0, 0, .... Типичной конфигурацией в процессе вычисления является

R1	R2	R3	R4	R5	...
x + k	y	k	0	0	...

Определим алгоритм следующим образом:

I1	J(3, 2, 5)
I2	S(1)
I3	S(3)
I4	J(1, 1, 1)

Заданный алгоритм вычисляет функцию x + y.

Пример 3.3. Докажите МНР-вычислимость функции

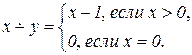
Решение. Составим алгоритм для начальной конфигурации x, 0, 0, .... Типичной конфигурацией в процессе вычисления является:

R1	R2	R3	R4	R5	...
x	k	k + 1	0	0	...

Следующий алгоритм МНР-вычисляет функцию.

I1	J(1, 2, 6)
I2	S(2)
I3	J(1, 2, 6)
I4	S(3)
I5	J(1, 1, 2)
I6	T(3, 1)

Упражнения

а) б) в)

Упражнение

3.4. Докажите разрешимость следующих предикатов на множестве целых неотрицательных чисел:

а) x = y;

б) ;

в) x < y;

г) x – четное число.

За последние пятьдесят лет было предложено много математических уточнений интуитивного понятия «алгоритм». Подход, основанный на МНР, является одним из них. Между этими подходами имеются большие различия, и в то же время все эти подходы эквивалентны между собой в том же смысле, что каждое уточнение алгоритма приводит к одному и тому же классу вычислимых функций.

Возникает теперь вопрос: насколько хорошо неформальное интуитивное понятие вычислимой функции отражено в различных формальных описаниях? Этот вопрос подвергался математиками серьезному обсуждению, в результате которого было высказано утверждение, известное под названием «тезис Черча»: каждая функция, вычислимая посредством процесса, алгоритмический характер которого интуитивно ясен, является вычислимой функцией. Применительно к нашему изложению этот тезис можно перефразировать следующим образом: всякая функция, для которой существует алгоритм (в интуитивном смысле) вычисления ее значений, является МНР-вычислимой функцией.

Сразу же заметим, что это утверждение не является теоремой, подлежащей математическому доказательству; оно имеет статус утверждения, принимаемого как постулат, справедливость которого подтверждается рядом свидетельств. Во-первых, таким свидетельством является то, что, как уже отмечалось, многие независимые уточнения интуитивного понятия вычислимой функции привели к одному и тому же классу функций. Во-вторых, никому не доводилось найти функцию, которую можно признать вычислимой в интуитивном смысле и которая не была бы МНР-вычислимой. Исходя из этих соображений и собственного опыта, большинство математиков приняли тезис Черча.

Нумерация программ для МНР

Определение 4.2. Множество называют не более чем счетным, если оно счетно или конечно. Определение 4.3. Перечислением или нумерацией множества X называется… Перечисление f определяет на множестве X некоторую бесконечную последовательность элементов из X такую, что каждый из…

Нумерация вычислимых функций

Из определения 5.1 следует, что каждая n-местная вычислимая функция f представлена в перечислении Ниже мы в основном будем рассматривать одноместные вычислимые функции . Для…

Упражнение

5.1. Докажите, что у каждой вычислимой функции имеется бесконечно много индексов.

Приступим теперь к доказательству теоремы о существовании невычислимых функций. Идея доказательства этой теоремы столь же важна, как и результат.

Теорема 5.1. Существует невычислимая всюду определенная функция.

Доказательство. Пусть 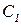- некоторое перечисление всех вычислимых функций:

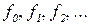
Положим

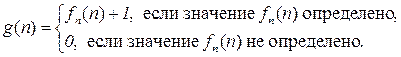
Функция g отличается от любой вычислимой функции в точке n. Действительно, если функция определена в точке n, то . Если не определена в точке n, то g отличается от тем, что значение g(n) определено. Таким образом, 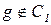и, следовательно, g - невычислимая всюду определенная функция.

Метод построения функции в теореме 5.1 является примером диагональной конструкции, открытой Кантором. Лежащая в его основе идея является центральной в доказательстве большинства результатов, связанных с вычислимостью функций, и применима к огромному числу ситуаций, возникающих в различных разделах математики.

Поясним, почему для примененного в теореме 5.1 метода выбран термин диагональный. Для этого проиллюстрируем метод построения функции g с помощью следующей бесконечной таблицы:

	0	1	2	3	...
					...
					...
					...
					...
...	...	...	...	...	...

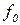
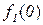
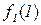
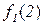
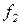
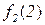
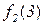
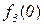
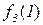
Рис. 5.1. Диагональная конструкция

При построении функции g для определения значений в точках n выбирались диагональные элементы таблицы . Выбранные значения изменялись так, чтобы обеспечить отличие g(n) от .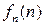

Очевидно, что новые значения функции можно выбирать сравнительно свободно. Например, функция

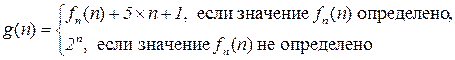
является другой невычислимой всюду определенной функцией.

Проиллюстрируем диагональную конструкцию на примере из теории множеств.

Пример 5.1. Докажем, что множество всех подмножеств множества 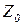нельзя перечислить (перенумеровать).

От противного, пусть - перечисление всех подмножеств множества 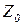. Определим новое подмножество B множества 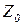следующим образом:

.

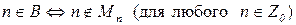Очевидно, 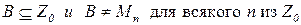, что противоречит предположению. Поэтому множество всех подмножеств множества 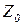нельзя перечислить.

Из доказанного вытекает, что множество всех подмножеств множества 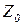несчетно.

Упражнения

5.2. Используя диагональный метод, докажите что множество всех функций из N в N несчетно (Кантор).

5.3. Докажите, что множество всех невычислимых всюду определенных функций из N в N несчетно.

Универсальные программы

Определение 6.1. Универсальной функцией для n-местных вычислимых функций называется (n+1)-местная функция . Для примера рассмотрим функцию . Эта функция реализует все одноместные вычислимые функции . Действительно, для…

Алгоритмически неразрешимые проблемы

При доказательстве неразрешимости той или иной проблемы часто используется так называемый метод сводимости, заключающийся в следующем. Пусть,… Ниже доказывается неразрешимость ряда известных проблем. Теорема 7.1. Проблема «функция всюду определена» неразрешима.

S-m-n-теорема

Теорема 8.1 (s-m-n-теорема, простая форма). Пусть f(х, у) -вычислимая функция. Существует всюду определенная вычислимая функция s(x), такая, что… Доказательство. Из вычислимости функции f(х, у) следует существование… в конфигурацию R1 R2 R3 R4 ... a y 0 0 …

Упражнения

8.2. 2. Покажите, что не существует всюду определенной вычислимой функции f(x, y), обладающей следующим свойством: если программа останавливается,… Указание. Покажите, что если бы такая функция существовала, то проблема… Естественно задаться вопросом, какие свойства вычислимых функций можно алгоритмически распознать по их программам.…