Универсальные программы

В этом разделе мы докажем несколько неожиданный результат, состоящий в том, что существуют универсальные программы, то есть программы, которые в некотором смысле реализуют все другие программы. Этот результат является одним из основных результатов теории вычислимости.

Определение 6.1. Универсальной функцией для n-местных вычислимых функций называется (n+1)-местная функция

.

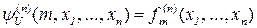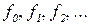Для примера рассмотрим функцию . Эта функция реализует все одноместные вычислимые функции . Действительно, для произвольного неотрицательного целого числа т функция совпадает с функцией . Таким образом, название функции вполне соответствует классу вычисляемых ею одноместных функций.

Ниже для простоты вместо будем писать .

Теорема 6.1. Для каждого натурального числа n универсальная функция вычислима.

Доказательство. Покажем, как можно вычислить значение функции 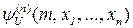для заданного числа m и фиксированного набора (x₁, ..., x_n). Неформальная процедура вычисления значения 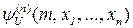состоит в следующем: «Декодируйте число m и восстановите программу Р_m. Затем имитируйте вычисление по этой программе. Если вычисление по программе заканчивается, требуемое значение 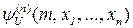содержится в регистре R₁». По тезису Черча заключаем, что функция вычислима.

Определение 6.2. Любая программа Р⁽ⁿ⁾, вычисляющая функцию , называется универсальной программой.

Универсальные программы полностью соответствуют своему названию. Действительно, так как универсальная программа Р⁽ⁿ⁾ позволяет вычислить любую n-местную вычислимую функцию, то, по сути дела, программа Р⁽ⁿ⁾ заменяет абсолютно все программы для вычисления n-местных функций.

Проиллюстрируем теперь, как использовать вычислимость универсальных функций в диагональных построениях.