Алгоритмически неразрешимые проблемы
Основным стимулом, приведшим к выработке понятия алгоритма и созданию теории алгоритмов, явилась потребность доказательства неразрешимости многих проблем, возникших в различных областях математики. Специалист, решая задачу, всегда должен считаться с возможностью того, что она может оказаться неразрешимой.
При доказательстве неразрешимости той или иной проблемы часто используется так называемый метод сводимости, заключающийся в следующем. Пусть, например, в результате некоторых рассуждений удалось показать, что решение проблемы Pr1 приводит к решению другой проблемы Pr2. В этом случае говорят, что проблема Pr2 сводится к проблеме Pr1. Таким образом, если проблема Pr2 сводится к проблеме Pr1, то из разрешимости Pr1 следует разрешимость Pr2 и, наоборот, из неразрешимости Pr2 следует неразрешимость Pr1. В данном разделе метод сводимости используется при доказательстве теоремы 7.3.
Ниже доказывается неразрешимость ряда известных проблем.
Теорема 7.1. Проблема «функция  всюду определена» неразрешима.
всюду определена» неразрешима.
Доказательство. Пусть g - характеристическая функция этой проблемы

Нам надо показать, что функция g невычислима.
От противного, предположим, что g - вычислимая функция. Рассмотрим функцию

Функция f всюду определена и отличается от каждой вычислимой функции  .
.
Применяя g и универсальную функцию  , запишем f в виде:
, запишем f в виде:

Из вычислимости функций g и  по тезису Черча следует вычислимость функции f.
по тезису Черча следует вычислимость функции f.
Полученное противоречие доказывает невычислимость функции g. Таким образом, проблема «функция  всюду определена» неразрешима.
всюду определена» неразрешима.
Обозначим область определения  и множество значений
и множество значений  функции
функции  через
через 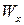 и
и 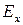 соответственно.
соответственно.
Теорема 7.2. Проблема «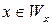 » неразрешима.
» неразрешима.
Доказательство. Характеристическая функция этой проблемы задается следующим образом:

Предположим, что функция g вычислима, и приведем это предположение к противоречию.
Рассмотрим функцию

Так как функция g вычислима, то по тезису Черча функция f также вычислима. С другой стороны, для любого x область определения Dom(f) функции f отлична от области определения 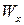 , и, следовательно,
, и, следовательно,  .
.
Таким образом, предположение о вычислимости характеристической функции g неверно. Поэтому проблема «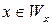 » неразрешима.
» неразрешима.
Замечание 7.1. Доказанная теорема вовсе не утверждает, что мы не можем для любого конкретного числа a сказать, будет ли определено значение  . В теореме лишь утверждается, что не существует единого общего метода решения вопроса о том, будет ли значение
. В теореме лишь утверждается, что не существует единого общего метода решения вопроса о том, будет ли значение  определено.
определено.
Замечание 7.2. Проблему «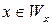 » называют также проблемой самоприменимости. Такое название связано с формулировкой проблемы в форме: «Остановится ли МНР, работая по программе
» называют также проблемой самоприменимости. Такое название связано с формулировкой проблемы в форме: «Остановится ли МНР, работая по программе  с начальной конфигурацией (x)?». Другими словами: «Применима ли программа к своему кодовому номеру?».
с начальной конфигурацией (x)?». Другими словами: «Применима ли программа к своему кодовому номеру?».
Теорема 7.3. Проблема « » неразрешима.
» неразрешима.
Доказательство. Если бы проблема « » была разрешима, то была бы разрешима более простая проблема «
» была разрешима, то была бы разрешима более простая проблема «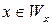 », что противоречит доказанной выше теореме.
», что противоречит доказанной выше теореме.
Замечание 7.3. Доказанную теорему часто интерпретируют как утверждение о неразрешимости проблемы остановки, в которой говорится, что не существует общего метода, устанавливающего, остановится ли некоторая конкретная программа, запущенная с некоторым конкретным набором начальных данных.
Смысл этого утверждения для теоретического программирования очевиден: не существует общего метода проверки программ на наличие в них бесконечных циклов.
В доказательстве теоремы мы показали, что проблема остановки « », по крайней мере, не проще, чем проблема самоприменимости «
», по крайней мере, не проще, чем проблема самоприменимости «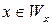 ». Мы свели вопрос о неразрешимости одной проблемы к другой. Это прием часто используется при доказательстве неразрешимости проблем.
». Мы свели вопрос о неразрешимости одной проблемы к другой. Это прием часто используется при доказательстве неразрешимости проблем.