S-m-n-теорема

В этом разделе мы докажем теорему, принадлежащую к числу основных результатов теории алгоритмов. Суть теоремы в следующем. Допустим, что f(х, у) - вычислимая функция. Для каждого фиксированного значения a переменной х функция f порождает одноместную вычислимую функцию g_a(y) = f(a, у). Из вычислимости функции g_a следует существование индекса b такого, что f(a, у) = f_b(у). Оказывается индекс b можно эффективно вычислить по параметру а.

Теорема 8.1 (s-m-n-теорема, простая форма). Пусть f(х, у) -вычислимая функция. Существует всюду определенная вычислимая функция s(x), такая, что f(х, у) = f_s(x)(у).

Доказательство. Из вычислимости функции f(х, у) следует существование МНР-программы Pr, которая, исходя из начальной конфигурации (x, y, 0, 0, ...), вычисляет значение функции f от двух аргументов х и у. Изменим программу Pr, добавив спереди команды, преобразующие начальную конфигурацию

R1	R2	R3	R4	...
y	0	0	0	...		(*)

в конфигурацию

R1	R2	R3	R4	...
a	y	0	0	...

следующим образом:

T(1, 2)

Z(1)

Pr

Новая программа Pr1, примененная к начальной конфигурации (*), вычисляет значение функции g_a(y) = f(a, у) от одного аргумента у.

Теперь рассмотрим функцию s(a) = g(Pr1), сопоставляющую произвольному неотрицательному целому числу a геделев номер программы Pr1. Функция s всюду определена и по тезису Черча вычислима. Кроме того, по построению f_s(a)(у) = f(a, у) для каждого .

Замечание 8.1. Сформулированную теорему называют также теоремой параметризации, поскольку она позволяет по заданной вычислимой функции f(x, у) и фиксированному параметру a найти геделев номер s(a) программы, вычисляющей функцию f_s(a)(у) = f(a, у).

Доказанная выше теорема 8.1 является частным случаем более общей теоремы.

Теорема 8.2 (s-m-n-теорема). Пусть m, n – натуральные числа, 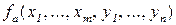- вычислимая функция с геделевым номером a. Существует всюду определенная вычислимая функция 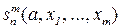такая, что

.

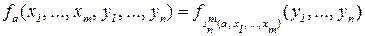Доказательство сформулированного утверждения аналогично доказательству теоремы 8.1.

Замечание 8.2. Название теоремы 8.2 связано с обозначением 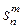для функций в формулировке теоремы.

Покажем теперь, как можно использовать s-m-n-теорему для доказательства неразрешимости проблем. s-m-n-теорема часто используется для сведения проблемы «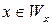» к другим проблемам.

Теорема 8.3. Проблема «» неразрешима.

Доказательство. Рассмотрим функцию

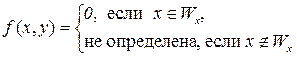
По тезису Черча функция f(x, y) вычислима. Отсюда по s-m-n-теореме вытекает существование всюду определенной вычислимой функции s(x) такой, что 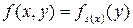. По определению функции f(x, y) имеем:

.

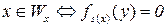Следовательно, истинность условия 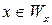можно установить, определив справедливость равенства . Тем самым мы свели проблему «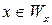» к проблеме «». Поскольку первая из них неразрешима, то неразрешима и вторая.

Замечание 8.3. Теорема 8.3 показывает, что в области проверки правильности компьютерных программ имеются принципиальные ограничения. В ней говорится о том, что не существует алгоритма проверки того, будет ли программа вычислять нулевую функцию. Несколько изменив доказательство теоремы 8.3, можно убедиться в том, что то же самое справедливо и для любой другой конкретной вычислимой функции.

Теорема 8.4. Проблема 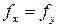неразрешима.

Доказательство. Допустим, что проблема 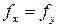разрешима. Тогда разрешима и проблема , где c – индекс функции 0 . Однако, это противоречит теореме 8.3. Таким образом, проблема 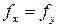неразрешима.

Замечание 8.4. Из теоремы 8.4 следует, что вопрос о том, вычисляют ли две программы одну и ту же одноместную функцию, неразрешим. Важность этого результата для теоретического программирования очевидна.