Интерпретации и модели аксиоматической теории
Формулируя аксиомы в примерах предыдущего пункта, нами не учитывалась природа элементов тех множеств, которые там встречаются, а также природа других первоначальных понятий этих аксиоматических теорий.
Определение 4.1. Приписывание значений первичным понятиям аксиоматической теории называется интерпретацией теории. Если некоторая совокупность объектов и соответствий между ними, выбранных в качестве значений первоначальных понятий аксиоматической теории, то есть в качестве ее интерпретации, удовлетворяет всем аксиомам теории, то она называется моделью данной аксиоматической теории (или моделью системы аксиом теории).
Другими словами, интерпретация теории - просто отображение f, областью определения которого является множество Т первоначальных понятий этой теории. Если же образ f(T) удовлетворяет всем аксиомам теории, то это есть модель данной теории.
Так для теории эквивалентности ее моделями служат:
· множество действительных чисел R, рассматриваемое вместе с отношением равенства;
· множество прямых плоскости, рассматриваемое вместе с отношением параллельности;
· множество фигур плоскости, рассматриваемое вместе с отношением подобия;
· отношение «быть родственниками» на множестве людей.
Множество людей, рассматриваемое вместе с отношением «быть похожими» является интерпретацией теории эквивалентности, но не является ее моделью, так как в ней не выполняется аксиома транзитивности B3.
Обычная евклидова плоскость (плоскость, которая изучается на уроках геометрии в школе) является моделью теории аффинных плоскостей.
Другая модель аффинной плоскости возникает, если:
· в качестве множества точек выбрать совокупность упорядоченных пар действительных чисел (x, y);
· в качестве множества прямых - совокупность упорядоченных троек действительных чисел [a, b, c] таких, что a и b не равны 0 одновременно;
· считать точку (x, y) инцидентной (принадлежащей) прямой [a, b, c] в том и только в том случае, если ax + by + c = 0.
Приведем еще одну модель аффинной плоскости, состоящую из конечного числа объектов. Рассмотрим граф, приведенный на рисунке 4.1.
Рис. 4.1. Модель аффинной плоскости
Вершины графа будем считать точками аффинной плоскости, ребра графа – прямыми. Точку M будем считать инцидентной прямой l, если вершина графа, соответствующая точке M, принадлежит ребру, соответствующему прямой l.
В последней несколько необычной модели пять прямых изображены прямолинейными отрезками, а шестая прямая CB – отрезком кривой. При этом прямая CB по определению параллельна прямой AD.
Существуют и другие модели приведенных теорий. В такой возможности по-разному интерпретировать аксиоматические теории заключена одна из причин обширных приложений этих теорий в других науках и в практике.
Определение 4.2. Две модели некоторой аксиоматической теории называются изоморфными, если между множествами основных объектов этих моделей можно установить взаимно однозначное отображение, сохраняющее основные соответствия.
Пусть, например, в одной из двух моделей какое-либо основное соответствие имеет значение 
, а в другой 
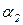. Тогда, если объекты x1 и y1 первой модели связаны соответствием , то соответствующие им объекты x2 и y2 и второй модели должны быть связаны соответствием 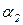(и обратно):
.
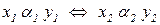Пример 4.1. Теория AT. Рассмотрим аксиоматическую теорию, в которой, подобно теории аффинных плоскостей, первичными понятиями служат: точка, прямая и инцидентность. За аксиомы примем следующие предложения:
C1. Любые две различные точки инцидентны хотя бы одной прямой.
C2. Любые две различные точки инцидентны не более чем одной прямой.
C3. Любой прямой инцидентны хотя бы две точки.
C4.Существуют три точки, не инцидентные одной прямой.
Рассмотрим некоторые модели теории AT.
Модель (а). Сопоставим первичным понятиям теории конкретные термины модели в соответствии с таблицей
| Первичные понятия теории | Термины модели |
| Точка | Шарик |
| Прямая | Стержень |
| Точка инцидентна прямой | Шарик надет на стержень |
На рисунке 4.2 представлена модель теории из трех шариков и трех стержней.
Рис. 4.2. Модель (а)
Модель (б). Точки – стержни, прямые – шарики, смысл отношения инцидентности – прежний.
Модель (в). Точки – четыре вершины тетраэдра, прямые – шесть ребер тетраэдра, точка считается инцидентной прямой, если вершина является концом ребра. (Можно было принять за точки грани тетраэдра, а за прямые – его ребра).
Модель (г). Точки – числа 2, 3, 5, прямые – числа 6, 10, 15, точка A считается инцидентной прямой b, если b делится на A.
Модель (д). Точки – числа 1, 2, 3, прямые – числовые множества {1, 2}, {1, 3}, {2, 3}, инцидентность понимается как принадлежность в теоретико-множественном смысле.
Модель (е). Точки и прямые – это любые точки и прямые трехмерного евклидова пространства; инцидентность понимается также, как в евклидовой геометрии.
Модели (а) и (в) не изоморфны. Это следует из того, что между множествами первичных объектов моделей нельзя установить взаимно однозначное соответствие. По этой же причине не изоморфны модели (а) и (е).
Модели (а) и (г) изоморфны. Действительно, если установить взаимно однозначное соответствие следующим образом:
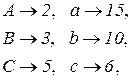
то оно будет сохранять инцидентность.
Аналогично доказывается изоморфизм моделей (а) и (б), а также (б) и (д).
Пример теории AT показывает, что использование аксиоматического метода позволяет установить связи между очень далекими, на первый взгляд, друг от друга областями. Вследствие существования различных моделей одной и той же системы аксиом, основанная на этой системе абстрактная теория может найти самые разнообразные применения.