Linear Operations on Vectors
Definition. The product of a vector  and a real number l is the vector
and a real number l is the vector 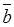 defined by the following conditions:
defined by the following conditions:
(1) 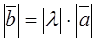 ;
;
(2) The vector  is collinear to
is collinear to  ;
;
3. The vectors  and
and  have the same direction if λ>0 and opposite directions if λ<0. If λ=0, then the direction of the vectors is arbitrary.
have the same direction if λ>0 and opposite directions if λ<0. If λ=0, then the direction of the vectors is arbitrary.


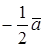 3
3
Property 1.For any numbers α and β and any vector  ,
,
α(β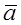 )= (αβ)
)= (αβ) 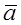 .
.
The vectors on both sides have the same length 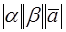 ; moreover they are collinear and have the same direction. Their direction coincides with the direction of
; moreover they are collinear and have the same direction. Their direction coincides with the direction of  if α and β are of the same sign and is opposite to the direction of
if α and β are of the same sign and is opposite to the direction of 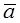 if α and β have opposite signs.
if α and β have opposite signs.
This length equals either  or
or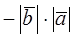 , depending on the directions of the vectors. If
, depending on the directions of the vectors. If 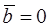 , then
, then  . The uniqueness on he multiplier l is evident: multiplying
. The uniqueness on he multiplier l is evident: multiplying  by different numbers, we obtain different vectors.
by different numbers, we obtain different vectors.
Definition.Suppose that  and
and 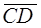 are vectors and ε is a point such that
are vectors and ε is a point such that 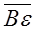 =
= . Then the vector
. Then the vector 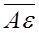 is called the sum of the vectors
is called the sum of the vectors  and
and  and denoted by
and denoted by  +
+

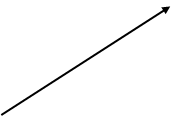
 ε
ε

 Â
 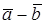


 A D
A D 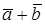
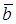
C
Property 2.Addition of vectors is commutative; this means that, for any two vectors,
 =
=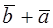 .
.
Property 3.Addition of vectors is associative; this means that, for any vectors,
 .
.
Property 4.Addition is distributive with respect to multiplication by a number; i.e., for any vectors  and
and  and any number a,
and any number a,
 .
.
To prove these properties, it is sufficient to refer to the triangle rule:


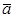
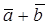
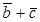

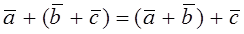 .
.
Property 5.For any numbers a and b and any vector  ,
,
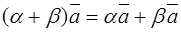 .
.
The vectors on both sides are collinear.
Suppose that a and b are of the same sign. Then the vectors a and b
and b have the same direction, and the length is equal to the sum of their lengths, i.e.,
have the same direction, and the length is equal to the sum of their lengths, i.e., 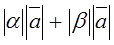 .
.
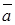
 a
a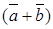

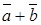

a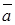
But  ; thus, in this case, the vectors
; thus, in this case, the vectors 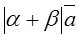 and a
and a +b
+b have the same length.
have the same length.
Their direction coincides with that of the vector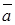 if the sign of a and b is positive, and is opposite to that of
if the sign of a and b is positive, and is opposite to that of  if the sign is negative.
if the sign is negative.
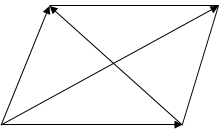
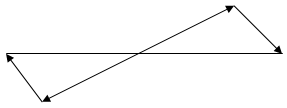
Definition. Free vectors are vectors which can be translated, which means that they do not depend on the head but are determined by direction and length.
B 
 B1 B
B1 B
A A1 A
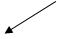
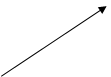
Consider vectors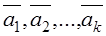 , their sum
, their sum  is determined by one vector, whose head coincides with that of the first vector and the tail with that of the last vector.
is determined by one vector, whose head coincides with that of the first vector and the tail with that of the last vector.


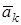
 ,
,


 .
.



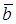

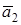

Definition. The ort-vector of a vector  is the vector of unit length whose direction coincides with that of
is the vector of unit length whose direction coincides with that of  .
.



 is the ort-vector of
is the ort-vector of  .
.

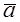
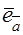
Subtraction of vectors can be considered as the addition of two vectors, the second of which is taken with the sign –:
 .
.
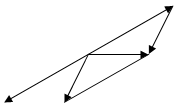

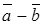
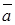

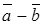

Theorem.If two vectors  and
and  can be represented as
can be represented as

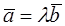 , (1)
, (1)
Then these vectors are collinear, and vice versa, if two vectors are collinear, then they relation (1) holds.
Proof. Suppose that (1) holds. If 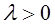 , then
, then 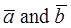 have the same direction, and consequently, lie on the same straight line or on parallel lines, i.e., are collinear.
have the same direction, and consequently, lie on the same straight line or on parallel lines, i.e., are collinear.
Conversely, suppose that vectors are collinear: 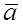 ÷÷
÷÷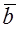 . Then they can be placed on the same straight line, and the first vector is longer than the other second one by a factor of
. Then they can be placed on the same straight line, and the first vector is longer than the other second one by a factor of  . Consequently,
. Consequently, 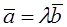 .
.
 Â
Â
À φ
φ l
À1 Â1
Definition.The projection of a vector onto an axis is defined as the length of the interval whose endpoints are the projections of the endpoints of the vector onto this axis which is taken with the sign + if the angle between the vector and the axis is acute and with this sign – if this angle is obtuse:
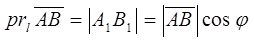 .
.
The projection of the sum of vectors is equal to the sum of the projections of the vectors:
 .
.


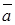
l
1. Suppose that n vectors 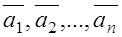 are given. These n vectors are said to be linearly dependent if one of them can be represented as a linear combination of the other vectors:
are given. These n vectors are said to be linearly dependent if one of them can be represented as a linear combination of the other vectors:
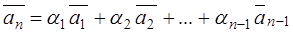 .
.
2. These n vectors are said to be linearly dependent if there exist numbers  (
(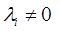 for some i) such that they can be represented as
for some i) such that they can be represented as
 =0.
=0.