Chapter 2. Analytic Geometry

Chapter 2. Analytic Geometry

§ 2.1. Vector Algebra. Operations on Vectors

 

Definition. A directed interval (or an ordered pair of points) is called a vector.

В

А

 

Definition.A vector with coinciding endpoints is called the null vector.

Definition. The distance between the head and tail of a vector is called the length, or absolute value of this vector. It is denoted by or.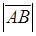

Definition.Vectors are collinear if they lie on the same straight line or on parallel lines.

 

A B C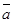

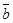
are collinear vectors,

А₁ В₁

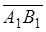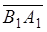, are collinear vectors.

 

Definition.Vectors are coplanar if they lie in the same plane or in parallel planes.

Definition.Two vectors are said to be equal if they are collinear and have the same direction and length.

 

Linear Operations on Vectors

(1) ; (2) The vector is collinear to ; 3. The vectors and have the same direction if λ>0 and opposite directions if λ<0. If λ=0, then…

Decomposition of vectors.

. Proof.Consider the parallelogram with sides parallel to the vectors and . We… ,

А

Theorem 2. An arbitrary vector in space can be decomposed into three noncoplanar vectors

.

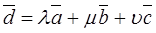Let be noncoplanar vectors.

Prove this theorem using a similar picture in space.

2.1.3. The Cartesian system of coordinates. Consider the following coordinate system: take mutually perpendicular unit vectors 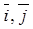and , draw coordinate axes x,y and z along them, and fix a unit on metric scale:

,

.

 

 

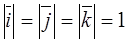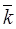
Definition. The triple of vectors 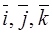is called right if, looking from the endpoint of the last vector, we see that the shorter rotation from the first vector to the second is anticlockwise.

From the triangle ОММ₁, we obtain

,

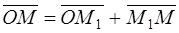Since the vector 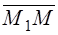is collinear to the unit vector 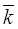, it follows that

.

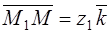From the triangle ОАМ_1, we obtain

,

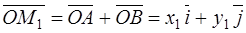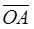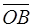because, by analogy, the vectors and are collinear to the unit vectors 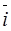and 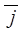. Substituting the vector thus obtained, we see that

. (2)

Thus, the radius vector is represented as the sum of and multiplied by the corresponding coordinates of the point М.

Consider the vectors

and

and their sum

.

Under addition the respective coordinates are added

Let us multiply the vector by a number l:

.

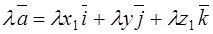When a vector is multiplied by a number l, each coordinate of this vector is multiplied by this number.

. (2¢) Example. Find the vectorif ; .

Inner Product of Vectors and its Properties

. (4) A

The inner product of vectors in coordinates. Consider two vectors

The last property allows us to multiply these vectors term by term: .

The inner product of vectors is equal to the sum of products of their coordinates.

Example 2. and . Then . Let us derive a formula for the length of a vector by using inner product:

The direction of a vector. Let us find the angle between two vectorsand .

. We have . (*)

Vector Product and Its Properties

We have considered a product of two vectors equal to a number (inner product) . What happens if the product of two vectors is a vector:

.

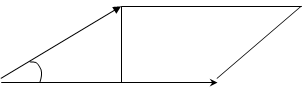
Proof. Consider the parallelogram spanned by the vectors and :

h

j

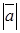
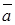
By the determination of vector product, its absolute value is

,

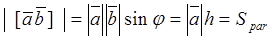where the height of the parallelogram is defined by

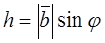(theopposite leg),

as required.

2. The vector product is anticommutative, i.e.,

.

j

–

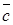
Proof.Let us denote the vector products under consideration by

and .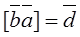

Consider the absolute value of the vector product on the right–hand side:

=.

 

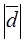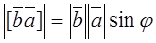This coincides with (*). I.e., these vector products have equal absolute values.

According to the definition of vector product, we have

 

,

 

and the triple of vectors 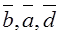must be right. But the rotation from to is clockwise. Thus, for the third condition in the definition to be satisfied, it we must take the vector –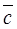instead of and look from below, which proves the required property.

3. To multiply a vector product by a number l, it is suffices to multiply one of the vectors by this number (without proof):

.

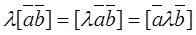4. Vector product is associative:

 

.

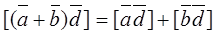The proof is left to the reader.

5. The vector product of collinear vectors is equal to zero, and vice versa, if the vector product of two vectors is zero, then these vectors are collinear.

Proof1. If vectors and are collinear, i.e., 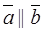, then 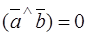or p, and the sine of this angle vanish. Hence 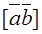=0.

2. Suppose that 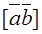=0 but and .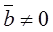

Then 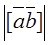=0. It follows that sinj=0, i.e., and are collinear.