Inner Product of Vectors and its Properties
Definition. The inner product of two vectors  and
and  is the product of the absolute values of these vectors and the cosine of the angle between them:
is the product of the absolute values of these vectors and the cosine of the angle between them:
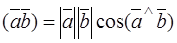 . (4)
. (4)
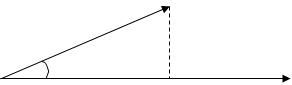 A
A

0φ
Property 1.Theinner product of two vectors is equal to the product of the absolute value of one vector and the projection of the second vector onto the first, i.e.,
 . (5)
. (5)
Proof.It is seen from the figure that the projection of the vector  on the vector
on the vector  is the interval
is the interval 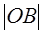 , whose length is equal to
, whose length is equal to  , because this is the adjacent leg. The inner product equals
, because this is the adjacent leg. The inner product equals  , as required.
, as required.
The remaining equalities in (5) are proved in a similar way.
Formula (5) easily implies the projection of the vector  on the vector
on the vector  :
:
 .
.
Property 2. The inner product of two vectors is equal to zero if and only if these vectors are perpendicular.
1. If 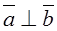 , then
, then  , and the inner product equals
, and the inner product equals 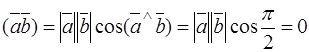 .
.
2. Conversely, suppose that 
(a) If both vectors are nonzero (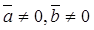 ) and
) and 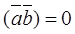 , then
, then  . Consequently, ñosj=0, and j=90î, i.e.
. Consequently, ñosj=0, and j=90î, i.e. 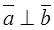 , as required.
, as required.
(b) Suppose that one of the vectors is zero, say, 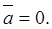
Since a null vector has no direction, we may assume that this null vector is perpendicular to the vector  , as required.
, as required.
Property 3. The inner product of vectors is commutative:
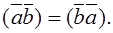
Proof. Let us decompose the right- and left-hand sides:
 ;
; 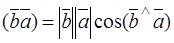 .
.
Since the angles between the two pairs of vectors are equal ( ), it follows that their cosines are equal; consequently, the left- and right-hand sides are equal.
), it follows that their cosines are equal; consequently, the left- and right-hand sides are equal.
Property 4. To multiply an inner product by a number l, it is sufficient to multiply one of the factors by l:
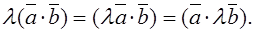
(Without proof.)
Property 5.Inner product is associative:
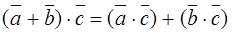 .
.
Proof.Applying property 1, formula (5), and the projection of the sum of the vectors to the right-hand side, we obtain
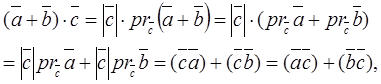
as required.