The direction of a vector. Let us find the angle between two vectorsand .
Consider the inner product
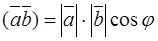 .
.
We have
 . (*)
. (*)
Writing the product and absolute values in coordinates, we obtain
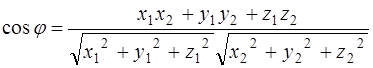 . (**)
. (**)
Example 3. Find an angle between vectors 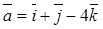 and
and  . By using formula (**), we find
. By using formula (**), we find
 ,
, 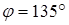
Example 4. Find the ort-vector  for the vector
for the vector 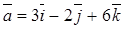 .
.
Let us determine a condition for vectors to be perpendicular. Suppose that vectors  and
and  are perpendicular, i.e.,
are perpendicular, i.e.,  ; then
; then  , and
, and
 . (7)
. (7)
 This is the condition for vectors to be perpendicular.
This is the condition for vectors to be perpendicular.
z

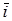 0
0  y
y
x
Consider the angles between a vector  and the unit vectors
and the unit vectors 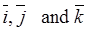 . We denote these angles by
. We denote these angles by
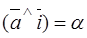 ;
;  ;
;  .
.
Take the product of 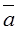 and any unit vector, say,
and any unit vector, say, 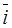 =
=
 .
.
By formula (*), the cosine of the angle a from it is
 .
.
Similarly the cosines of the other angles are
 ,
, 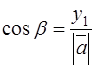 ,
, 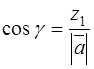 . (8)
. (8)
These cosines are called the directional cosines of the vector .
.
The sum of the squared directional cosines equals one:
 .
.
To prove this, it sufficies to square the cosines by formula (8) and sum them:
 .
.
Example 5. For what a are the vectors
 and
and 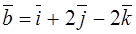
perpendicular?
We use the perpendicularity condition (7) and write the inner product of the given vectors in coordinates:
 ;
;  , a=10.
, a=10.
Example 6. Given the vectors  and
and  , find the inner product
, find the inner product  .
.






 ,
,  .
.
The required product is
 .
.
Example 7. Prove that the sum of the squared lengths of the diagonals in a parallelogram equals the sum of the squared sides of this parallelogram (by using inner product).
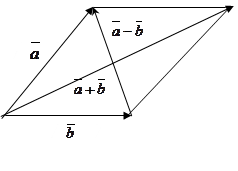 Consider the parallelogram
Consider the parallelogram
The sum of the inner squares of the diagonals equals
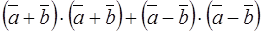
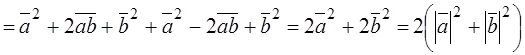 .
.
Since, the inner square of a vector equals the square of its absolute value, we obtain
 .
.