Статистическая модель. Сущность статистического моделирования
4.1.1. Статистическая модель.При статистическом (стохастическом) моделировании основными объектами моделирования являются случайные события, случайные величины и случайные функции.
При проведении экспериментов исследователь фиксирует появление или не появления интересующих событий, а также осуществляет измерения значений параметров, которые носят случайный характер и по своей сути являются значениями реализации некоторой случайной величины.
Статистическое моделирование дает возможность не проводя реальных экспериментов над исследуемым объектом (что в большинстве случаев требует больших материальных и финансовых затрат) получать соответствующую информацию о появлении или не появлении тех или иных событий происходящих в реальном объекте. о выборочных значениях случайных величин на основе имеющихся вероятностных характеристик моделируемых событий и случайных величин. Данный вид моделирования предполагает проведение предварительного сбора информации о моделируемых показателях и дальнейшей статистической обработки полученных результатов с целью получения обоснованных статистических оценок, требуемых для моделирования вероятностных характеристик.
Стохастические модели применяются в основном в двух случаях:
1) объект моделирования плохо изучен – не имеется достаточно хорошо разработанных количественных закономерностей, описывающих рассматриваемые процессы и явления, а так же нет возможности найти приемлемое аналитическое решение данной проблемы;
2) моделируемый объект изучен достаточно хорошо в детерминированном плане, но без учета случайных факторов, оказывающих влияние на изучаемые процессы и явления.
В первом случае на основе словесного описания исследуемого объекта производится выбор количественных показателей с расчетом их физической размерности состоящих из двух групп. Одна из групп рассматривается в качестве входных величин модели, а другая – выходных величин. Далее, применяя научные теоретические результаты полученные другими исследователями в данной области и возможно применяя ряд необходимых допущений, а так же возможно уже имеемые экспериментальные данные о входных и выходных величинах (например, об их законах распределения) устанавливают детерминированные или стохастические зависимости между входными выходными величинами модели. Совокупность полученных соотношений между входными и выходными величинами (обычно записываются в виде уравнений) называют статистической моделью.
В ходе реализации статистической модели на основе выбранных законов распределения случайных величин и выбранными вероятностями моделируемых событий методами математической статистики определяются выборочные до экспериментальные значения случайных величин и квазиэмпирические последовательности появления или не появления моделируемых событий. Далее, по уравнениям модели определяют соответствующие выборочные значения ее выходных величин. А многократная реализация построенной модели позволяет исследователю построить модельную выборку ее выходных величин, которая вновь подвергается статистическому анализу (корреляционному, регрессивному, дисперсионному, спектральному) с целью получения оценок характеристик выходных параметров модели или проверки выдвигаемых гипотез. На основе полученных результатов делаются заключения по объекту исследования, а также обоснования по практическому применению построенной модели.
Методы статистического моделирования широко применяются при решении задач массового обслуживания, теории оптимизации, теории управления, теоретической физике и т.д.
Теоретической основой метода статистического моделирования [1,9,18, 19, 20] на компьютере являются предельные теоремы теории вероятностей.
4.1.2. Неравенство Чебышева. Для неотрицательной функции  случайной величины
случайной величины  и
и  выполняется неравенство
выполняется неравенство
 .
.
4.1.3. Теорема Бернулли. Если проводятся 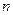 независимых испытаний, в каждом из которых некоторое событие
независимых испытаний, в каждом из которых некоторое событие 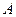 осуществляется с вероятностью
осуществляется с вероятностью 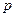 , то относительная чистота появления события
, то относительная чистота появления события  (
( число благоприятных исходов испытания) при
число благоприятных исходов испытания) при 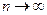 сходится по вероятности к
сходится по вероятности к 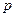 , т.е. при
, т.е. при 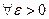
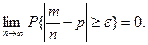
4.1.4. Теорема Пуассона. Если проводятся 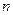 независимых испытаний и вероятность осуществления события
независимых испытаний и вероятность осуществления события 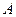 в
в 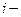 том испытании равна
том испытании равна  , то относительная чистота появления события
, то относительная чистота появления события  (
( число благоприятных исходов испытания) при
число благоприятных исходов испытания) при 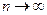 сходится по вероятности к среднему из вероятностей
сходится по вероятности к среднему из вероятностей  , т.е. при
, т.е. при 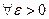

4.1.5. Теорема Чебышева. Если в 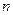 независимых испытаниях наблюдаются значения
независимых испытаниях наблюдаются значения  случайной величины
случайной величины  , то при
, то при 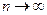 среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию
среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию  , т.е. при
, т.е. при 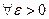
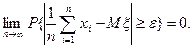
4.1.6. Обобщенная теорема Чебышева. Если 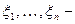 независимые случайные величины с математическими ожиданиями
независимые случайные величины с математическими ожиданиями  и дисперсиями
и дисперсиями 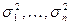 ограниченными сверху одним и тем же числом, то при
ограниченными сверху одним и тем же числом, то при 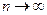 среднее арифметическое значений случайной величины сходится по вероятности к среднему арифметическому их математических ожиданий
среднее арифметическое значений случайной величины сходится по вероятности к среднему арифметическому их математических ожиданий

4.1.7. Теорема Маркова.. Теорема Чебышева будет справедлива и для зависимых случайных величин 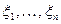 , если
, если

4.1.8. Центральная предельная теорема. Если 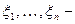 независимые одинаково распределенные случайные величины с математическое ожидание
независимые одинаково распределенные случайные величины с математическое ожидание 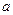 и дисперсию
и дисперсию 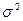 , то при
, то при 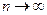 закон распределения суммы
закон распределения суммы  неограниченно приближается к нормальному закону распределения
неограниченно приближается к нормальному закону распределения
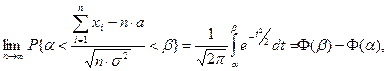
где  функция Лапласа [18,19,20]
функция Лапласа [18,19,20]
4.1.9. Теорема Лапласа. Если в каждом из 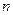 независимых испытаний событие
независимых испытаний событие 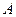 появляется с вероятностью
появляется с вероятностью 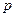 , то
, то
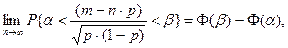
где  число появления события
число появления события 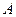 в
в 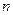 испытаниях.
испытаниях.
Приведем пример задачи, для решения которой применим метод статистического моделирования.
Задача. Проводится 10 независимых выстрелов по мишени. Вероятность попадания при одном выстреле равна 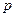 . Требуется оценить вероятность, того, что число попаданий в мишень будет четной..
. Требуется оценить вероятность, того, что число попаданий в мишень будет четной..
Решение. Данная задача является вероятностной, причем существует и аналитическое решение
 .
.
Каждый выстрел есть не, что иное, как результат значения случайной величины равномерно распределенной на интервале (0;1), причем, если это значение не превосходит 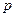 , то произошло попадание в мишень, а в противном случае сделан промах. Таким образом, для построения моделирующего алгоритма необходим генератор значений случайной величины равномерно распределенной на интервале (0;1), который выдает нам при каждом испытании серию из десяти чисел (имитирует 10 выстрелов)
, то произошло попадание в мишень, а в противном случае сделан промах. Таким образом, для построения моделирующего алгоритма необходим генератор значений случайной величины равномерно распределенной на интервале (0;1), который выдает нам при каждом испытании серию из десяти чисел (имитирует 10 выстрелов) 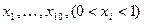 . Подсчитываем количество попаданий
. Подсчитываем количество попаданий  где
где  номер испытания, а
номер испытания, а 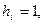 если
если  и
и  четное, то
четное, то  , а в противном случае
, а в противном случае 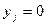 . Проведя
. Проведя  испытаний, получаем оценку искомой вероятности
испытаний, получаем оценку искомой вероятности
 .
.