Моделирование непрерывных случайных величин.
4.6.1. Моделирование случайной величины имеющей равномерный закон распределения. Случайная величина  имеет равномерный закон распределения на
имеет равномерный закон распределения на 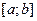 , если она имеет плотность распределения
, если она имеет плотность распределения 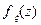 вида
вида
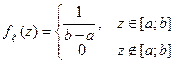 ,
,
и функцию распределения 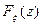 вида
вида
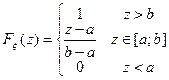 .
.
Введем обозначение 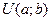 - семейство случайных величин равномерно распределенных на
- семейство случайных величин равномерно распределенных на 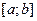 .
.
Теорема 2.Если 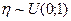 и
и 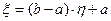 , то
, то 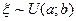 .
.
Доказательство. По определению функции распределения
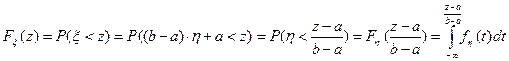
Так как 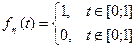
Тогда 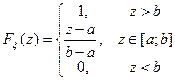 . Теорема доказана.
. Теорема доказана.
Следствие.Если последовательность чисел 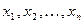 является выборкой случайной величины
является выборкой случайной величины 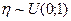 , то последовательность
, то последовательность 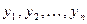 , где
, где 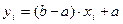 является выборкой значений случайной величины
является выборкой значений случайной величины 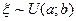 .
.
4.6.2. Метод обратной функции. Предположим, что случайная величина  определена в интервале
определена в интервале 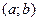 и имеет плотность
и имеет плотность 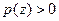 при
при 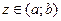 . Обозначим через
. Обозначим через 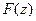 функцию распределения
функцию распределения  , которая при
, которая при 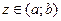 равна
равна
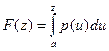 .
.
Случай 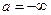 и (или)
и (или) 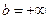 не исключается.
не исключается.
Теорема 3.Пусть случайные величины 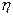 и
и  удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
а) 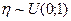 ;
;
б) 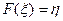 . (5)
. (5)
Тогда случайная величина  имеет плотность распределения
имеет плотность распределения 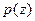 .
.
Доказательство. По определению функция распределения 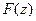 строго возрастает в интервале
строго возрастает в интервале 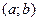 от
от 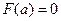 до
до 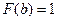 , тогда уравнение (5) будет иметь единственный корень при каждом конкретном значении случайной величины
, тогда уравнение (5) будет иметь единственный корень при каждом конкретном значении случайной величины 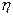 . При этом будут равны вероятности
. При этом будут равны вероятности
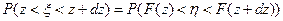 .
.
И так как случайная величина 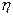 равномерно распределена в интервале
равномерно распределена в интервале 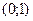 , то
, то
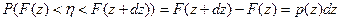 .
.
Следовательно  . Что и требовалось доказать.
. Что и требовалось доказать.
В тех случаях, когда уравнение (5) аналитически разрешимо относительно  , получается явная формула
, получается явная формула 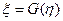 для моделирования случайной величины
для моделирования случайной величины  , где
, где 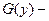 обратная функция по отношению к
обратная функция по отношению к 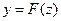 . В других случаях уравнение (5) решают численными методами.
. В других случаях уравнение (5) решают численными методами.
Пример. (Моделирование случайной величины имеющей показательное или экспоненциальное распределение). Пусть  случайная величина, имеющая показательное распределение (обозначение
случайная величина, имеющая показательное распределение (обозначение 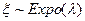 ). Функция распределения имеет вид
). Функция распределения имеет вид
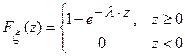 .
.
Задаем 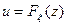 и находим обратную функцию
и находим обратную функцию 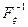 :
:
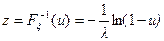 .
.
Следовательно, для генерирования искомой случайной величины, сначала генерируют случайную величину 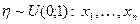 - выборка данной случайной величины. Затем определяют последовательность чисел
- выборка данной случайной величины. Затем определяют последовательность чисел
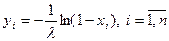 , (6)
, (6)
которая и будет являться реализацией случайной величины  .
.
4.6.3. Универсальный способ. Данный способ основан на аппроксимации функции плотности случайной величины.
Пусть требуется получить реализацию случайной величины  , которая имеет функцию плотности,
, которая имеет функцию плотности,  и множество значений данной функции есть интервал
и множество значений данной функции есть интервал 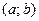 . Представим
. Представим  в виде кусочно-постоянной функции. Для этого разобьем интервал
в виде кусочно-постоянной функции. Для этого разобьем интервал 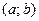 на
на 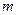 интервалов и будем считать, что
интервалов и будем считать, что  на каждом таком интервале является постоянной. Тогда случайную величину
на каждом таком интервале является постоянной. Тогда случайную величину  можно представить в виде
можно представить в виде 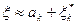 , где
, где 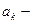 абсцисса левой границы
абсцисса левой границы 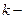 того интервала, а
того интервала, а 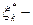 случайная величина, возможные значения которой располагаются равномерно внутри
случайная величина, возможные значения которой располагаются равномерно внутри 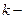 интервала, то есть на интервале
интервала, то есть на интервале 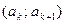 , а величина
, а величина 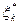 считается распределенной равномерно. Для аппроксимации функции
считается распределенной равномерно. Для аппроксимации функции  целесообразно разбиение интервала
целесообразно разбиение интервала 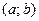 осуществить так, чтобы вероятность попадания случайной величины
осуществить так, чтобы вероятность попадания случайной величины  в любой интервал
в любой интервал 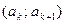 была постоянной, то есть не зависела от номера интервала
была постоянной, то есть не зависела от номера интервала 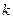 . Таким образом, для вычисления
. Таким образом, для вычисления 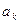 необходимо воспользоваться следующим соотношением
необходимо воспользоваться следующим соотношением
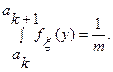
Алгоритм моделирования случайной величины  (получение
(получение 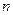 значений):
значений):
1. Генерируется случайная последовательность равномерно распределенных чисел 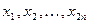 (
(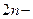 чисел) из интервала (0; 1).
чисел) из интервала (0; 1).
2. 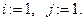
3. С помощью числа 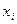 случайным образом выбирается интервал
случайным образом выбирается интервал 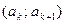 :
:  .
.
4. С помощью числа 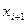 вычисляем значение случайной величины
вычисляем значение случайной величины  :
: 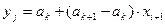 .
.
5. Если 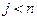 , то увеличиваем индексы
, то увеличиваем индексы 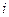 и
и 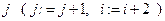 , и переходим к пункту 3 данного алгоритма, в противном случае алгоритм заканчивает свою работу.
, и переходим к пункту 3 данного алгоритма, в противном случае алгоритм заканчивает свою работу.
6. Числа 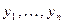 являются значениями реализации случайной величины
являются значениями реализации случайной величины  .
.
4.6.4. Способы, базирующиеся на предельных теоремах теории вероятностей. Такие способы ориентированы на моделирование случайных величин с конкретным законом распределения. Поясним сказанное на примерах.
Пример 1. Необходимо получить последовательность случайных чисел 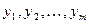 , имеющих нормальное распределение с математическим ожиданием
, имеющих нормальное распределение с математическим ожиданием 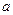 и дисперсией
и дисперсией 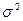 . Иными словами промоделировать случайную величину
. Иными словами промоделировать случайную величину 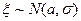 .
.
Воспользуемся центральной предельной теоремой 4.1.8. Промоделируем независимые одинаково распределенные случайные величины 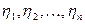 , которые имеют одинаковые математические ожидания
, которые имеют одинаковые математические ожидания 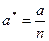 и средне квадратичное отклонение
и средне квадратичное отклонение 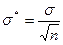 , то сумма
, то сумма 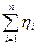 асимптотически нормальна с математическим ожиданием
асимптотически нормальна с математическим ожиданием 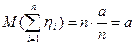 и дисперсией
и дисперсией 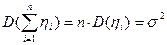 . В ходе моделирования случайных величин
. В ходе моделирования случайных величин 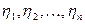 нами будут получены их числовые реализации
нами будут получены их числовые реализации 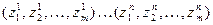 , где
, где 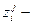 это
это 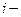 тая реализация
тая реализация 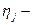 той случайной величины
той случайной величины 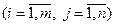 . Тогда
. Тогда 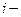 той реализацией случайной величины
той реализацией случайной величины  будет
будет 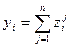 .
.
Пример 2. Необходимо промоделировать случайную величину, имеющую распределение Пуассона
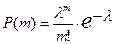 .
.
Для этого воспользуемся предельной теоремой Пуассона (4.1.1): если 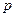 вероятность наступления события
вероятность наступления события 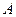 при одном испытании, то вероятность наступление события
при одном испытании, то вероятность наступление события 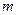 раз в
раз в 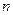 независимых испытаниях при
независимых испытаниях при  асимптотически равна
асимптотически равна 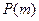 .
.
Алгоритм моделирования 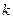 чисел имеющих закон распределения Пуассона:
чисел имеющих закон распределения Пуассона:
1. Зададим достаточно большое натуральное число 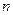 и
и 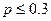 ,
, 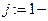 номер числа.
номер числа.
2. Проводим серию 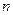 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 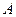 происходит с вероятностью
происходит с вероятностью 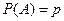 . Определяем число случаев
. Определяем число случаев 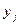 фактического наступления события
фактического наступления события 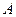 в серии с номером
в серии с номером 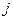 .
.
3. Если 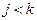 , то
, то 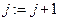 возвращаемся к пункту 2 алгоритма, в противном случае алгоритм завершает свою работу.
возвращаемся к пункту 2 алгоритма, в противном случае алгоритм завершает свою работу.
4. Числа 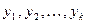 являются значениями реализации случайной величины распределенной по закону Пуассона.
являются значениями реализации случайной величины распределенной по закону Пуассона.
4.6.5. Аналитические способы. Используют результаты других разделов математики и основываются на строгих аналитических доказательствах. Один из таких способов применен в разделе 4.7 при обосновании алгоритма моделирования случайной величины имеющей стандартное нормальное распределение.