Аналитические методы.
Теорема 4.Пусть  и
и  случайные величины, равномерно распределенные на отрезке
случайные величины, равномерно распределенные на отрезке 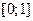 . Из данных случайных величин образуем случайную величину
. Из данных случайных величин образуем случайную величину  , случайную величину
, случайную величину 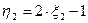 , и случайную величину
, и случайную величину  . Введем случайную величину,
. Введем случайную величину,  заданную по правилу
заданную по правилу
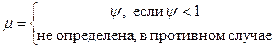 .
.
Тогда случайные величины  и
и 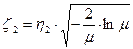 являются независимыми и имеют стандартное нормальное распределение.
являются независимыми и имеют стандартное нормальное распределение.
Доказательство. Все значения пары случайных величин  при условии
при условии  являются координатами точек, равномерно распределенных внутри единичного круга. Тогда данные случайные величины могут быть выражены через полярные координаты
являются координатами точек, равномерно распределенных внутри единичного круга. Тогда данные случайные величины могут быть выражены через полярные координаты  ,
,  , где
, где  . Следовательно,
. Следовательно,  и
и  . Таким образом,
. Таким образом, 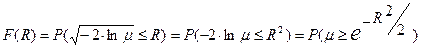 . Поскольку по построению
. Поскольку по построению  равномерно распределена на отрезке
равномерно распределена на отрезке 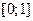 , то
, то  и плотность распределения вероятностей
и плотность распределения вероятностей  . Найдем совместную функцию распределения для
. Найдем совместную функцию распределения для 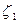 и
и 
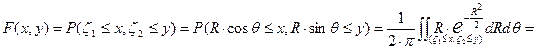

Теорема доказана.
Алгоритм моделирования 1 ( стандартно нормально распределенных чисел ):
стандартно нормально распределенных чисел ):
1. и
и  .
.
2. Моделируем две независимые случайные величины, равномерно распределенные на [0; 1] реализацией которых будут выборки чисел:  и
и  . Преобразуем данные последовательности в
. Преобразуем данные последовательности в 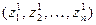 и
и  , где
, где  ,
,  .
.
3. Вычисляем величину .
.
4. Если 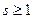 , то
, то 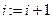 и возвращаемся к шагу 3, в противном случае переходим к шагу 5 алгоритма.
и возвращаемся к шагу 3, в противном случае переходим к шагу 5 алгоритма.
5. 
6. Если 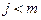 , то
, то 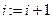 и возврат к шагу 3, в противном случае алгоритм завершает свою работу.
и возврат к шагу 3, в противном случае алгоритм завершает свою работу.
7. Последовательности случайных чисел  и
и  будут являться независимыми, и иметь стандартное нормальное распределение.
будут являться независимыми, и иметь стандартное нормальное распределение.
Теорема 5.Пусть случайная величина 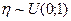 и
и 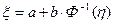 , где
, где  функция Лапласа, тогда
функция Лапласа, тогда  , то есть имеет нормальный закон распределения с параметрами
, то есть имеет нормальный закон распределения с параметрами  и
и  .
.
Доказательство. По определению функции распределения
 ,
,
где 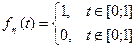 .
.
Следовательно,  . Таким образом, случайная величина
. Таким образом, случайная величина  имеет нормальный закон распределения с математическим ожиданием равным
имеет нормальный закон распределения с математическим ожиданием равным 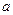 и среднеквадратичным отклонением равным
и среднеквадратичным отклонением равным 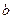 . Теорема доказана.
. Теорема доказана.
Следствие.Если последовательность случайных чисел 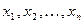 является выборкой равномерно распределенной на [0;1] случайной величины, то последовательность
является выборкой равномерно распределенной на [0;1] случайной величины, то последовательность  , где
, где  является выборкой случайной величины, имеющей нормальный закон распределения с математическим ожиданием равным
является выборкой случайной величины, имеющей нормальный закон распределения с математическим ожиданием равным 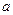 и дисперсией равной
и дисперсией равной  .
.
Теорема 6.Случайные величины  , а случайные величины
, а случайные величины  и
и  заданны формулами:
заданны формулами:  и
и  . Тогда случайные величины
. Тогда случайные величины  и являются независимыми.
и являются независимыми.
Доказательство теоремы проводится аналогично доказательству теоремы 5.
Алгоритм моделирования 2 (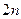 стандартно нормально распределенных чисел ):
стандартно нормально распределенных чисел ):
1.  .
.
2. Моделируем две независимые случайные величины, равномерно распределенные на [0; 1] реализацией которых будут выборки чисел:  и
и  .
.
3. Вычисляем величины  и
и 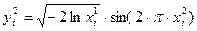 .
.
4. Если  , то
, то 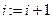 и возвращаемся к шагу 3, в противном случае переходим к шагу 5 алгоритма.
и возвращаемся к шагу 3, в противном случае переходим к шагу 5 алгоритма.
5. Алгоритм закончил свою работу: последовательности случайных чисел 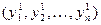 и
и 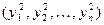 будут являться независимыми, и иметь стандартное нормальное распределение.
будут являться независимыми, и иметь стандартное нормальное распределение.
4.7.2. Приближенное моделирование нормального распределения.Рассмотрим нормированную сумму равномерно распределенных величин 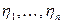 на интервале (0;1):
на интервале (0;1):
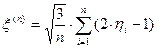 . (6)
. (6)
Согласно предельно теореме 4.1.8 при 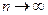
 .
.
Следовательно, по формуле (6) при достаточно больших 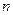 можно вычислять приближенное значение нормальной случайной величины с параметрами (0;1), таким образом
можно вычислять приближенное значение нормальной случайной величины с параметрами (0;1), таким образом  .
.