Решение линейного уравнения методом подстановки
Решение уравнения (20) будем искать в виде произведения двух функций от 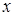

Подставим у и у' в уравнение (20):
 (22)
(22)
Сгруппируем слагаемые с  в первой степени (можно с u):
в первой степени (можно с u):

Выберем функцию  такой, чтобы множитель с
такой, чтобы множитель с 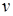 обращался в
обращался в  .
.

Таким образом, получим систему

Решая первое уравнение системы (уравнение с разделяющимися переменными относительно 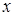 и
и  , найдем искомую функцию
, найдем искомую функцию  .
.
Так как одна из неизвестных функций  и
и  может быть выбрана произвольно, то в качестве
может быть выбрана произвольно, то в качестве  возьмем любое частное (ненулевое) решение уравнения
возьмем любое частное (ненулевое) решение уравнения 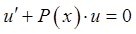 , а в качестве
, а в качестве  возьмем общее решение второго уравнения системы
возьмем общее решение второго уравнения системы  , в которое, прежде чем решать его, подставим найденную функцию
, в которое, прежде чем решать его, подставим найденную функцию  .
.
Общее решение уравнения (20) запишем в виде  , подставив найденные функции.
, подставив найденные функции.
Замечание. Если в уравнении (22) сначала вынести общий множитель u в первой степени, то искомые функции найдем в обратном порядке, вначале  , а потом
, а потом  .
.
Пример 12. Решить задачу Коши

Решение. Данное уравнение линейно относительно у и у' .

Решение ищем в виде

Подставим у и у' в уравнение
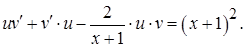
Вынесем 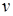 в первой степени за скобки
в первой степени за скобки
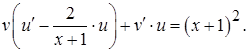
Полагаем 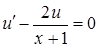 , тогда
, тогда 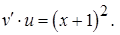
Таким образом, получим систему

Решаем первое уравнение системы, 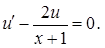 Это уравнение с разделяющимися переменными.
Это уравнение с разделяющимися переменными.

Интегрируя полученное уравнение, имеем
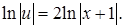
(постоянную интегрирования при нахождении  не вводим, т.к. достаточно найти любое (ненулевое) частное решение уравнения
не вводим, т.к. достаточно найти любое (ненулевое) частное решение уравнения 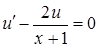 ).
).
Далее 
Подставим  во второе уравнение системы и найдем
во второе уравнение системы и найдем  :
:
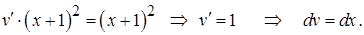
Интегрируя, получим общее решение второго уравнения системы:

Таким образом, общее решение данного линейного уравнения имеет вид:

Найдем частное решение уравнения. Используя начальное условие 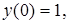 найдем с.
найдем с.
Подставив 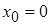 и
и 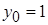 в общее решение линейного уравнения, получим
в общее решение линейного уравнения, получим

Тогда частное решение линейного уравнения при  имеет вид:
имеет вид:

Пример 13. Решить задачу Коши
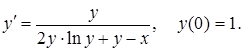
Решение. Данное уравнение нелинейно относительно  и
и 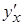 .
.
Преобразуем уравнение, воспользовавшись там, что 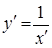 :
:

Полученное уравнение линейно относительно 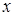 и
и  .
.
Решение будем искать в виде
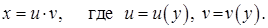
Тогда 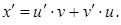
Подставим 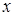 и
и  в уравнение
в уравнение



Вначале решаем первое уравнение системы
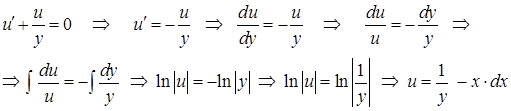
- частное решение первого уравнения системы.
Подставим  во второе уравнение системы
во второе уравнение системы  :
:

Вычислим отдельно каждый интеграл:
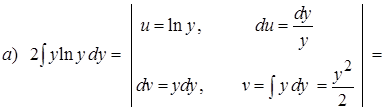
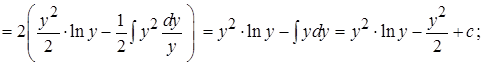
б) 
Подставляя решение этих двух интегралов в  , получим
, получим

Тогда, общее решение линейного дифференциального уравнения (23) имеет вид:
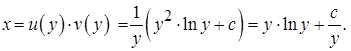
Воспользуемся начальными условиями  и найдем
и найдем  .
.

Тогда частное решение линейного уравнения (23) при  имеет вид:
имеет вид:
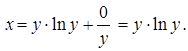
5. Уравнение Бернулли
Определение. Уравнение вида
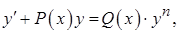 (24)
(24)
называется уравнением Бернулли, где  и
и 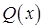 - непрерывные функции от
- непрерывные функции от 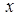 ,
,  ,
, 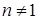 .
.
Замечание. При  получается линейное уравнение первого порядка относительно
получается линейное уравнение первого порядка относительно  и
и  , а при
, а при  получается уравнение с разделяющимися переменными.
получается уравнение с разделяющимися переменными.
Уравнение Бернулли приводится к линейному следующим образом:
Разделим все члены уравнения (24) на 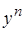

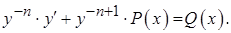 (25)
(25)
Сделаем замену: 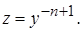
Тогда 
Подставим  в уравнение (25) вместо
в уравнение (25) вместо 

Умножим полученное уравнение на  :
:
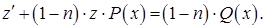 (26)
(26)