рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- МАТАНАЛИЗ 3
Реферат Курсовая Конспект
МАТАНАЛИЗ 3
МАТАНАЛИЗ 3 - раздел Образование, ...
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
УТВЕРЖДАЮ
Директор ИПР
_______________ Ю.Д. Дмитриев
«____»_____________2012 г.
МАТАНАЛИЗ 3
Методические указания и индивидуальные задания для студентов ИПР, обучающихся по направлениям и специальностям 131000 «Нефтегазовое дело», 130101 «Прикладная геология», 130102 «Технология геологической разведки», 022000 «Экология и природопользование»Аннотация
Методические указания и индивидуальные задания по дисциплине «Матанализ 3» предназначены для студентов ИПР, обучающихся по направлениям и специальностям 131000 «Нефтегазовое дело»,
130101 «Прикладная геология», 130102 «Технология геологической разведки»,
022000 «Экология и природопользование». Данная дисциплина изучается в одном семестре.
Приводится содержание основных тем дисциплины, темы практических занятий, варианты заданий для индивидуальных домашних заданий и список рекомендуемой литературы. Даны методические указания по выполнению индивидуальных домашних заданий.
 |
Учебное издание
МАТАНАЛИЗ 3
Методические указания и индивидуальные задания для студентов ИПР, обучающихся по направлениям и специальностям 131000 «Нефтегазовое дело», 130101 «Прикладная геология», 130102 «Технология геологической разведки», 022000 «Экология и природопользование»Отпечатано в Издательстве ТПУ в полном соответствии с качеством предоставленного оригинал-макета
I. Интегральное исчисление функции одной переменнойНеопределенный интеграл
Интегрирование рациональных функций методом разложения их на простейшие дроби. Интегрирование тригонометрических функций различных классов. Интегрирование алгебраических иррациональностей различных видов и дифференциального бинома.Определенный интеграл
Производная интеграла по верхнему пределу. Формула Ньютона-Лейбница. Вычисление определенного интеграла: интегрирование по частям, подстановкой. … Приложения определенного интеграла к вычислению площадей, длин дуг, объемов тел, вычисление работы.II. Дифференциальные уравнения
Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения. Понятие об особых решениях.
Уравнения с разделяющимися переменными. Однородное уравнение.
Линейное уравнение первого порядка. Уравнение Бернулли и в полных дифференциалах.
III. Числовые ряды
Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами.
Ряды с положительными членами. Признаки сходимости.
Знакопеременные ряды. Абсолютная и условная сходимость.
Знакочередующиеся ряды. Признак Лейбница.
IV. Функциональные ряды
Основные понятия. Область сходимости.
Понятие равномерной сходимости. Признак Вейерштрасса. Свойства равномерно сходящихся рядов.
V. Степенные ряды
Теорема Абеля. Свойства степенных рядов.
Разложение функций в степенные ряды.
Ряды Тейлора и Маклорена.
Применение рядов к приближенным вычислениям.
I. Интегральное исчисление функции одной переменной
Неопределенный интеграл
Например, одной из первообразных функций для функции будет . Первообразная не единственна, т. к. =+=, = , а поэтому , также являются первообразными… Теорема.Две различные первообразные одной и той же функции, определенной на… Следствие. Прибавляя к какой-либо первообразной для данной функции , определенной на промежутке, всевозможные…Основные свойства неопределенного интеграла
. 2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а… (1)Таблица интегралов





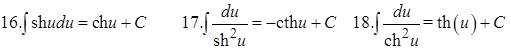
 Полезно помнить таблицу дифференциалов:
Полезно помнить таблицу дифференциалов:

Отметим несколько преобразований, полезных для отыскания первообразных:
1. 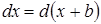 , где
, где  ;
;
2. 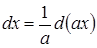 ,
,  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  .
.
и вообще:  . Эту формулу называют подведением множителя
. Эту формулу называют подведением множителя  под знак дифференциала. Используя таблицу интегралов и эти формулы, найдем некоторые интегралы.
под знак дифференциала. Используя таблицу интегралов и эти формулы, найдем некоторые интегралы.
Непосредственное интегрирование
Пример 1. . Выражение заменили на . Получили интеграл который можно отыскать в таблице… Пример 2. .Пример 4.
 ,
,
т. к.  , умножим и разделим подынтегральное выражение на –2. Здесь выражение
, умножим и разделим подынтегральное выражение на –2. Здесь выражение 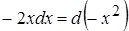 и получили табличный интеграл
и получили табличный интеграл 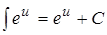 .
.
Проверка:  .
.
Метод подстановки
Пример 5. Найти . Чтобы избавиться от корня, полагаем , отсюда . Найдем . Для этого… Итак,Метод интегрирования по частям
, проинтегрировав это выражение, получим или . (5)Пример 7.
 =
= = подставляя в формулу (5) получим
= подставляя в формулу (5) получим
= =
=
 .
.
Иногда формула интегрирования по частям применяется несколько раз. Рассмотрим пример такого интеграла.
Пример 8. 
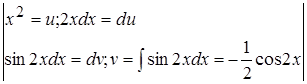 =
=
=
 =
=
= =
=
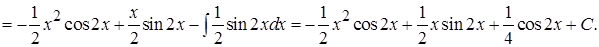 Здесь формулу интегрирования по частям мы применили к полученному интегралу
Здесь формулу интегрирования по частям мы применили к полученному интегралу еще раз.
еще раз.
Замечание. Иногда применение формулы интегрирования по частям приводит к исходному интегралу, который в таком случае называется циклическим или круговым.
Пример 9. Найти интеграл  =
= .
.
 Получили интеграл, в котором
Получили интеграл, в котором  заменился на
заменился на  .
.
Проинтегрируем еще раз по частям, обозначим:

Тогда  =
=
 ,
,
т.е. пришли к искомому интегралу 
Таким образом, 
Найдем 
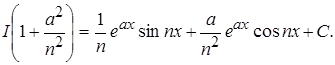
Упрощая, получим: 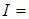

Это пример циклического интеграла.
Интегрирование рациональных дробей
Простейшими элементарными дробями называются дроби следующего вида: I. ; II. , >1, целое;Пример 10.
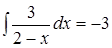
 , здесь
, здесь  .
.
Пример 11.
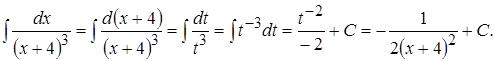
Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Пример 12.
 =
=

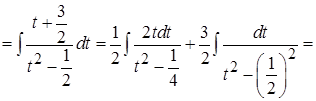
 ;
;
Возвращаясь к старой переменной, получим:

Алгоритм интегрирования рациональной дроби
2. Знаменатель разложим на простейшие сомножители: , где многочлены не имеют действительных корней. 3. Представим дробь в виде суммы простейших дробей с неопределенными коэффициентами.Примеры интегрирования рациональных функций
Пример 13.  =
= ;
;
 − это неправильная рациональная дробь. Сначала выделим целую часть дроби, разделив числитель на знаменатель.
− это неправильная рациональная дробь. Сначала выделим целую часть дроби, разделив числитель на знаменатель.
- 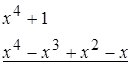
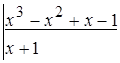
-
Тогда  , где
, где  – целая часть дроби,
– целая часть дроби, 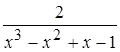 – правильная рациональная дробь, знаменатель которой разлагается на множители:
– правильная рациональная дробь, знаменатель которой разлагается на множители: 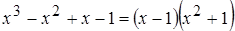 .
.
Корни знаменателя: 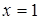 , а
, а  не имеют действительных корней.
не имеют действительных корней.
Тогда разложение для данной дроби имеет вид:
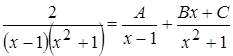 .
.
Приводя полученные дроби к общему знаменателю, получим тождество:
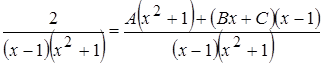 .
.
Приравнивая числители обеих дробей, получим уравнение:
2= .
.
Пусть 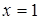 , тогда 2=2
, тогда 2=2
 . Коэффициенты
. Коэффициенты  найдем из системы:
найдем из системы:
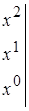

Откуда 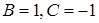 .
.
Тогда  =
= =
=
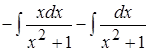 =
=
Пример 14. .
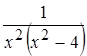 – правильная дробь. Разложим знаменатель на простейшие сомножители, получим:
– правильная дробь. Разложим знаменатель на простейшие сомножители, получим: 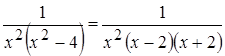 .
.
Корни знаменателя:  – кратности 2 и
– кратности 2 и 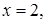
 – простые корни.
– простые корни.
Запишем разложение правильной рациональной дроби на сумму простейших:
 .
.
Приведем дроби к общему знаменателю, затем приравняем числители обеих дробей. Получим тождество:
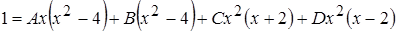 .
.
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.


Откуда 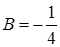 ,
,  ,
,  .
.
Чтобы найти коэффициент  составим уравнение, приравнивая коэффициенты при
составим уравнение, приравнивая коэффициенты при  слева и справа в тождестве.
слева и справа в тождестве.
Получим уравнение: 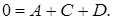 Откуда
Откуда  .
.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.


Интегрирование тригонометрических функций
I. где − рациональная функция от и . Это означает, что над аргументами производятся только рациональные операции: сложение, вычитание,… , . Следует заметить, что, применяя эту подстановку можно привести любую подынтегральную функцию к рациональной дроби, но…Пример 16.
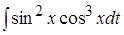 =
= =
= =
= ,
,
где 
Пример 17. 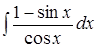 .
.
Применим универсальную тригонометрическую подстановку:
 ,
,  ,
,  ,
,  .
.
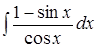
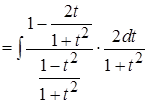
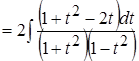

 ;
;
Разложим дробь 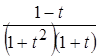 на простейшие
на простейшие
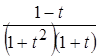
 ;
;
Откуда  .
.
Найдем коэффициенты разложения из системы:



 .
.
Проинтегрируем:
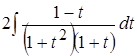

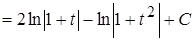

 .
.
IV. Если 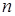 и
и  – дробные либо целые (отрицательные) числа и
– дробные либо целые (отрицательные) числа и  – целое отрицательное число, тогда рекомендуется подстановка
– целое отрицательное число, тогда рекомендуется подстановка 
 ,
, 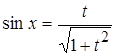 ,
, 
или

 ,
,  ,
,  .
.
Пример 18. 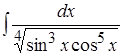
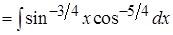 ;
;
т.к. 
 четное отрицательное число.
четное отрицательное число.
Используем подстановку  ,
,  ,
,  ,
,  ;
;


V. Интегралы вида  ,
,  , где
, где  >
> ,
, 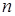 >0 вычисляются при помощи подстановки
>0 вычисляются при помощи подстановки  ,
,  и
и  ,
,  .
.
Пример 19.
 =
=
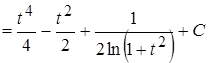
 ;
;
Т.к. дробь  – неправильная, то надо выделить целую часть дроби, поделив
– неправильная, то надо выделить целую часть дроби, поделив  на
на  .
.
 .
.
VI. Интегралы вида 

где  ,
, 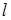 – действительные числа.
– действительные числа.
Напомним известные тригонометрические формулы:
 ;
;
 ;
;
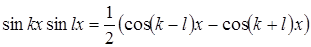 .
.
Заменив подынтегральные функции по этим формулам, получим интегралы, которые вычисляются просто.
Пример 20.  =
=
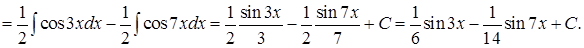 Интегрирование некоторых иррациональных функций
Интегрирование некоторых иррациональных функций
Определение 3. Функция называется алгебраической иррациональной, если над аргументом производится только четыре арифметических действия и действие возведения в рациональную степень.
Метод интегрирования алгебраических иррациональностей состоит в выборе подстановки, которая привела бы подынтегральную функцию к рациональной.
Наиболее часто встречаются иррациональности вида:
I.
1)  ;
;  – несократимые дроби.
– несократимые дроби.
Рекомендуется подстановка: 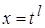 , где
, где 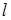 – наименьшее общее кратное знаменателей дробей
– наименьшее общее кратное знаменателей дробей  , (н.о.к.
, (н.о.к.  ).
).
2)  ;
;
Подстановка:  , где
, где  н.о.к.
н.о.к. .
.
3)  .
.
Подстановка:  , где
, где  н.о.к.
н.о.к.  приводит подынтегральную функцию к рациональному виду.
приводит подынтегральную функцию к рациональному виду.
II.
1) 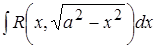 ; Подстановка:
; Подстановка: 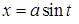 ,
,  .
.
2) 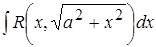 ; Подстановка:
; Подстановка:  ,
, 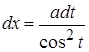 .
.
3)  ; Подстановка:
; Подстановка: 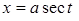 ,
,  .
.
III.
1)  приводится к одному из видов в п. II методом выделения полного квадрата трехчлена, стоящего под корнем квадратным.
приводится к одному из видов в п. II методом выделения полного квадрата трехчлена, стоящего под корнем квадратным.
Пример 21. 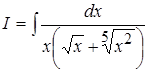
 ;
;
Наименьшее общее кратное знаменателей дробей 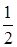 ,
,  равно 10.
равно 10.
Сделаем подстановку ,
,  ;
;
Тогда 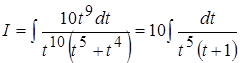 .
.
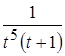 – правильная рациональная дробь. Разложим ее на простейшие рациональные дроби, что рекомендуется проделать самостоятельно.
– правильная рациональная дробь. Разложим ее на простейшие рациональные дроби, что рекомендуется проделать самостоятельно.
Получим:  =
=
=
 , где
, где 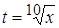 .
.
Пример 22. 
 ;
;
Сделаем подстановку, которая приводит подынтегральную функцию к рациональному виду: 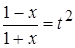 ;
;
Найдем из этого уравнения 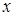 и
и 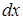 :
:
 ;
;  ;
;
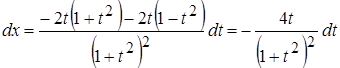 .
.
Тогда 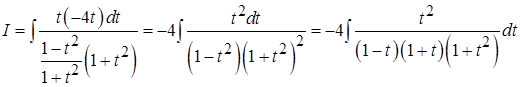 .
.
Проинтегрируем правильную рациональную дробь 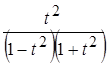 , разложив ее на простейшие дроби, используя метод неопределенных коэффициентов.
, разложив ее на простейшие дроби, используя метод неопределенных коэффициентов.
Представим интеграл в виде суммы: (рекомендуется выполнить самостоятельно),

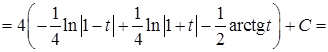
 .
.
Возвращаясь к старой переменной по формуле  ,
,
получим  .
.
Пример 23.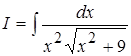 ; Это интеграл типа II.
; Это интеграл типа II.
Применим подстановку  ;
;  ;
;
 ;
;
тогда  ;
;
 ;
;
Чтобы вернуться к первоначальной переменной, выразим 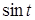 через
через  ;
;
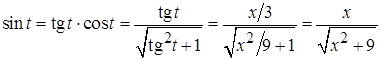 ;
;
Получим  ;
;
Пример 24.  ; Это интеграл типа III.
; Это интеграл типа III.
Алгоритм вычисления интеграла такого типа аналогичен алгоритму интегрирования рациональной дроби типа III:
 , а именно:
, а именно:
1) Выделение полного квадрата трехчлена, стоящего в знаменателе;
2) Введение новой переменной.
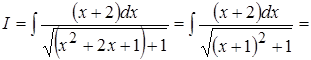
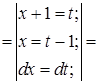



IV. Интеграл от дифференциального бинома:
 , может быть вычислен в конечном виде только в следующих случаях:
, может быть вычислен в конечном виде только в следующих случаях:
1) 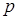 – целое число, тогда применима подстановка
– целое число, тогда применима подстановка 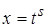 , где
, где  – общий знаменатель дробей
– общий знаменатель дробей  и
и 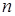 . Или разлагают на сумму по формуле бинома Ньютона.
. Или разлагают на сумму по формуле бинома Ньютона.
2)  – целое число, подстановка
– целое число, подстановка  , где
, где  – знаменатель дроби
– знаменатель дроби 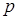 .
.
3)  – целое число, подстановка
– целое число, подстановка 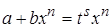 , где
, где  – знаменатель дроби
– знаменатель дроби 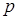 .
.
Эти подстановки называются подстановками Чебышева, который доказал, что только в этих случаях дифференциальный бином может быть приведен к рациональному виду и вычислен при помощи элементарных функций.
Пример 25.  ;
;
Запишем интеграл в виде  ,
,
где 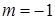 ,
,  ,
,  ,
,  .
.
 – не целое число;
– не целое число;  – целое число.
– целое число.
В этом случае применима подстановка:  ;
;
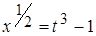 ;
; 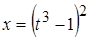 ;
;  ;
;
 ;
;
Проинтегрируем рациональную дробь: 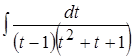 , разложив ее на простейшие:
, разложив ее на простейшие: 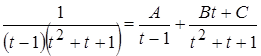 .
.
Найдя коэффициенты разложения, получим: А=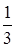 , B=
, B= , C=
, C= .
.
Подставим их в разложение и проинтегрируем дроби:
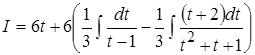 =
= ,
,
где  =
= .
.
Определенный интеграл
Рассмотрим частные случаи
. 2. Пусть непрерывна на . Разделим отрезок на произвольных частей точками .… Умножим найденные значения на длину , т.е. .Теорема существования определенного интеграла
Укажем на некоторые свойства определенного интеграла: 1. Определенный интеграл не зависит от обозначения переменной интегрирования… 2.Примеры 26.




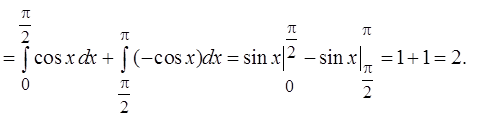
Формула Ньютона - Лейбница лежит в основе следующих методов, полезных при вычислении определенных интегралов.
Замена переменных в определенном интеграле
Пример 27. ПоложимИнтегрирование по частям
Или в обозначенияхНесобственные интегралы
от на и обозначается через . В этом случае говорят, что сходится.Примеры 29.
1) Вычислить:

2) Установить, при каких 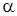 интеграл
интеграл  сходится?
сходится?
Пусть  . Тогда
. Тогда 
Таким образом, 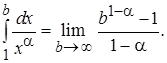
Значит, если 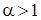 , то
, то 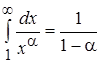 , т. е. интеграл сходится.
, т. е. интеграл сходится.
Если  , то
, то  , т. е. интеграл расходится.
, т. е. интеграл расходится.
При a=1,  , т. е. интеграл расходится.
, т. е. интеграл расходится.
3) 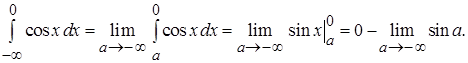
Интеграл расходится, т. к. предел не существует.
Пусть теперь функция непрерывна на интервале и . Если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают
Таким образом, по определениюФункция определена на , и то есть мы имеем дело с несобственным интегралом от функции с бесконечным разрывом.
то есть, расходится. Важную роль в решении вопроса о сходимости (расходимости) несобственного… Если функции и определены на интервале и для некоторого справедливо неравенство то из сходимости интеграла (из…Некоторые приложения определенного интеграла
Вычисление площади плоской фигуры
(8) Отметим, что если криволинейная трапеция расположена ниже оси 0х, , то площадь… (9)Примеры 32.
1) Вычислить площадь S фигуры, ограниченной кривыми 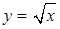 и
и  (см. рис. 5).
(см. рис. 5).
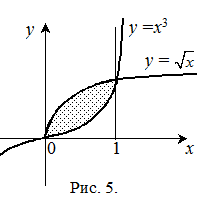
Находим точки пересечения кривых: 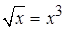 ,
, 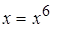 и, значит,
и, значит,  .
.
Следовательно


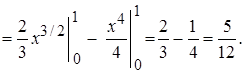
Вычислить площадь  фигуры, ограниченной эллипсом
фигуры, ограниченной эллипсом 

Сначала найдем площадь 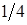 части эллипса (см. рис. 6).
части эллипса (см. рис. 6).
Здесь х изменяется от 0 до 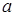 , следовательно,
, следовательно,  изменяется от
изменяется от  до 0.
до 0.
Находим, что

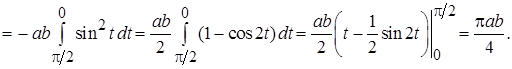
 Таким образом,
Таким образом,  .
.
2) Вычислить площадь S фигуры, ограниченной «трехлепестковой розой»:

Найдем вначале площадь половины одного лепестка «розы» (см. рис. 7).
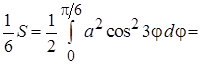


Следовательно, 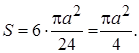
Длина дуги кривой
(13) Длина дуги АВ кривой L, заданной параметрическими уравнениямиПримеры 33.
1) 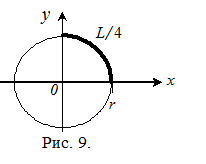 Найти длину окружности
Найти длину окружности  (см. рис. 9).
(см. рис. 9).
Вычислим длину окружности.
Вначале найдем L/4.
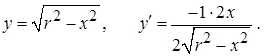
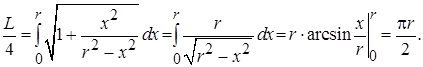
Длина окружности 
2) Вычислить длину дуги винтовой линии 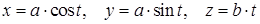 между точками
между точками 
Поскольку  , то
, то

 Найти длину кардиоиды
Найти длину кардиоиды 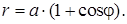
 Кардиоида имеет вид (см. рис. 10). Она симметрична относительно полярной оси
Кардиоида имеет вид (см. рис. 10). Она симметрична относительно полярной оси  .
.
Найдем половину длины кардиоиды L/2:

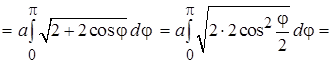

Длина кардиоиды 
Замечание.  на отрезке
на отрезке  .
.
Объем тела
Пример 34. Найти объем эллипсоида Рассекая эллипсоид плоскостью, параллельной плоскости и на расстоянии от неё…Объем тела вращения
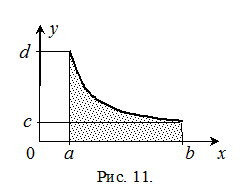 Объем тела, полученного вращением кривой вокруг оси ох
Объем тела, полученного вращением кривой вокруг оси ох
(см. рис. 11), определяется интегралом
 (15)
(15)
Аналогично, вокруг оси 0у.
Пример 35. Найти объем тела, образованного вращением фигуры, ограниченной линиями вокруг оси .Варианты заданий для контрольной работы № 3
Задание 1.Найти неопределенные интегралы.
1. В задачах 1 и 2 результат проверить дифференцированием.
2. В задачах 3 и 4 вычислить интегралы по формуле интегрирования по частям.
3. В задачах 5 и 6 проинтегрировать рациональные функции.
4. В задачах 7 и 8 найти интегралы от тригонометрических функций.
5. В задачах 9 и 10 вычислить интегралы, используя подходящую подстановку.
Вариант 1
1. ; 2.
; 2. ; 3.
; 3.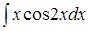 ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7.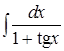 ;
;
8. ; 9.
; 9. ; 10.
; 10. 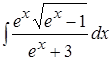 .
.
Вариант 2
1.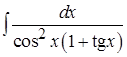 ; 2.
; 2.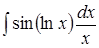 ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6.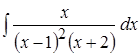 ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 3
1.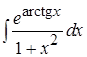 ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7.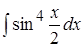 ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 4
1. ; 2.
; 2. 3.
3. 4.
4.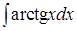
 ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9.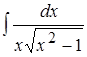 ; 10.
; 10. .
.
Вариант 5
1.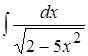 ; 2.
; 2.  ; 3.
; 3.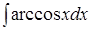 ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7.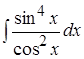 ;
;
8.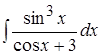 ; 9.
; 9.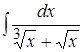 ; 10.
; 10. .
.
Вариант 6
1. 2.
2. 3.
3.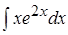 4.
4.
5. 6.
6. 7.
7.
8. 9.
9.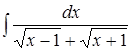 10.
10.
Вариант 7
1. ; 2.
; 2.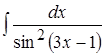 ; 3.
; 3. ; 4.
; 4.  ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.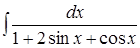 ; 9.
; 9.
 ; 10.
; 10.  .
.
Вариант 8
1.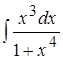 ; 2.
; 2. ; 3.
; 3. ; 4.
; 4.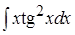 ;
;
5.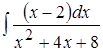 ; 6.
; 6.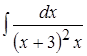 ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 9
1.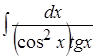 ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.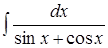 ; 9.
; 9. ; 10.
; 10.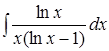 .
.
Вариант 10
1.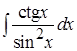 ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10.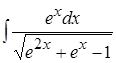
Вариант 11
1. ; 2.
; 2. ; 3.
; 3.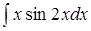 ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.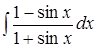 ; 9.
; 9.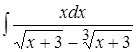 ; 10.
; 10. .
.
Вариант 12
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9.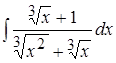 ; 10.
; 10.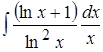 .
.
Вариант 13
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4.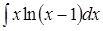 ;
;
5.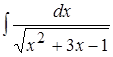 ; 6.
; 6. ; 7.
; 7. ;
;
8.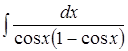 ; 9.
; 9.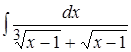 ; 10.
; 10. .
.
Вариант 14
1. ; 2.
; 2. ; 3.
; 3.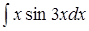 ; 4.
; 4.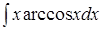 ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.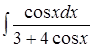 ; 9.
; 9. ; 10.
; 10.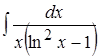 .
.
Вариант 15
1.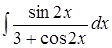 ; 2.
; 2. ; 3.
; 3.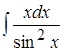 ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.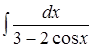 ; 9.
; 9. ; 10.
; 10. .
.
Вариант 16
1.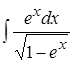 ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10.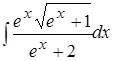 .
.
Вариант 17
1. ; 2.
; 2. ; 3.
; 3.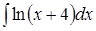 ; 4.
; 4. ;
;
5.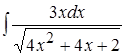 ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 18
1. ; 2.
; 2.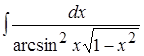 ; 3.
; 3.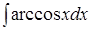 ; 4.
; 4.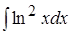 ;
;
5.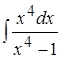 ; 6.
; 6. ; 7.
; 7.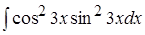 ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 19
1. ; 2.
; 2. ; 3.
; 3.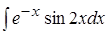 ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7.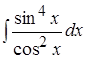 ;
;
8.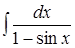 ; 9.
; 9. ; 10.
; 10.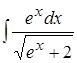 .
.
Вариант 20
1.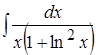 ; 2.
; 2. ; 3.
; 3.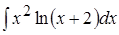 ;4.
;4.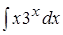 ;
;
5.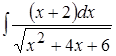 ; 6.
; 6.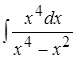 ; 7.
; 7.  ;
;
8. ; 9.
; 9.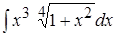 ; 10.
; 10. .
.
Задание 2.Вычислить определенный интеграл
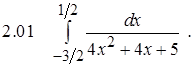


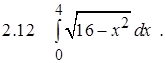

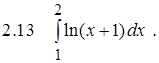




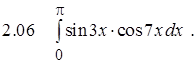


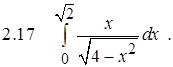



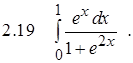
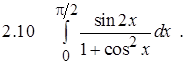

Задание 3. Вычислить несобственный интеграл или показать его расходимость.





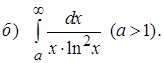


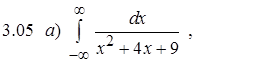

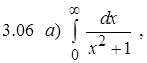




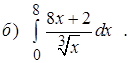


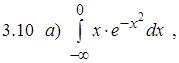

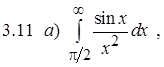


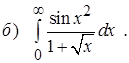

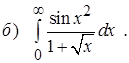







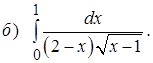






Задание 4. Вычислить площадь плоской фигуры, ограниченной линиями.

 (вне окружности)
(вне окружности) 



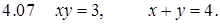







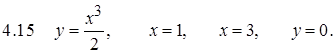



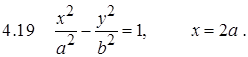
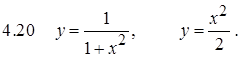
Задание 5. Вычислить длину дуги кривой.

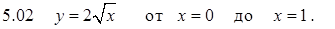



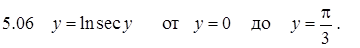




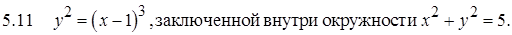
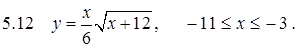





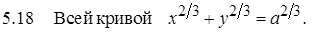

 .
.
Задание 6. Вычислить объем тела, образованного вращением вокруг оси 0х кривой, заданной уравнениями.



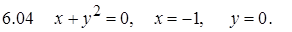



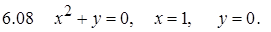






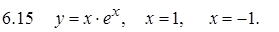

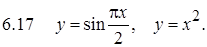
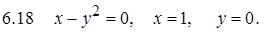



II. Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную , искомую функцию и её производную… Дифференциальное уравнение первого порядка имеет вид (1)Пусть в уравнении (2) функция и её частная производная непрерывны в некоторой области на плоскости . Тогда, какова бы ни была точка , всегда существует (и при том только одно) такое решение этого уравнения , которое равно при , т. к. .
Условие, что  при
при 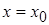 , называется начальным условием.
, называется начальным условием.
Оно записывается в виде
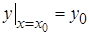 или
или 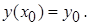 (5)
(5)
Поставим задачу. Найти решение 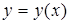 уравнения (2), удовлетворяющее предыдущей теореме.
уравнения (2), удовлетворяющее предыдущей теореме.
Такая задача называется задачей Коши.
Определение. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым.
Замечание. В некоторых случаях выгодно за искомую функцию считать переменную 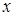 и записывать уравнение (2) в виде
и записывать уравнение (2) в виде
 где
где  (6)
(6)
Учитывая, что  и
и 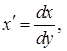 дифференциальные уравнения (1), (2) и (6) можно записать в форме
дифференциальные уравнения (1), (2) и (6) можно записать в форме
 (7)
(7)
где 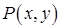 и
и 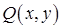 - известные функции.
- известные функции.
Пример 1. Найти общее решение уравнения 
Решение. Так как 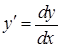 , то получим
, то получим 
Тогда  Интегрируя обе части уравнения, окончательно получим
Интегрируя обе части уравнения, окончательно получим 
Общее решение данного уравнения образует семейство кубических парабол, т.к.  может принимать любое числовое значение.
может принимать любое числовое значение.

Рассмотрим частное решение.
Пусть наша кривая проходит через точку М(1,0), см. рис. Подставим координаты точки М в общее решение. Получим
 , откуда
, откуда 
Тогда частное решение имеет вид

Геометрическое толкование дифференциального уравнения первого порядка заключается в том, что общее решение (общий интеграл) (4) представляет собой семейство кривых на координатной плоскости, зависящее от одной произвольной постоянной  .
.
Эти кривые называются интегральными кривыми уравнениями (1), (2).
Частному решению (задачи Коши) соответствует одна кривая этого семейства, проходящая через данную точку плоскости.
Решить дифференциальное уравнение (1) - значит:
1) найти его общее решение (если начальные условия не заданы);
2) найти частное решение уравнения (1), которое удовлетворяет начальным условиям или, другими словами, решить задачу Коши.
Рассмотрим некоторые типы дифференциальных уравнений первого порядка.
Уравнения с разделяющимися переменными
Определение. Дифференциальное уравнение вида
 (8)
(8)
в котором коэффициент при 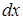 является функцией только от
является функцией только от 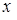 , а коэффициент при
, а коэффициент при 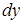 - функцией только от
- функцией только от  , называется уравнением с разделенными переменными.
, называется уравнением с разделенными переменными.
Функции 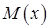 и
и  должны быть непрерывными для всех значений
должны быть непрерывными для всех значений 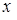 и
и  .
.
Уравнение с разделенными переменными решается следующим образом:
Перенесем слагаемое  в правую сторону равенства (8) с противоположным знаком.
в правую сторону равенства (8) с противоположным знаком.
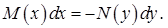
Проинтегрируем правую часть уравнения по  , а левую по х.
, а левую по х.
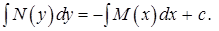 (9)
(9)
Полученное равенство (9) является общим интегралом уравнения с разделенными переменными (8).
Пример 2.Решить уравнение

Решение. Переменные уравнения разделены.
Тогда

Интегрируя, получим
 или
или 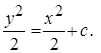
Тогда  или
или  - семейство гипербол.
- семейство гипербол.
Замечание. Дифференциалы 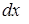 и
и  должны всегда стоять в числителе.
должны всегда стоять в числителе.
Определение. Дифференциальное уравнение вида
 (10)
(10)
в котором коэффициенты при дифференциалах можно разложить на множители, зависящие только от 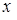 и только от
и только от  , называется уравнением с разделяющимися переменными.
, называется уравнением с разделяющимися переменными.
Разделим уравнение (10) на  ,
, 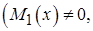
 получим
получим

Далее
 (11)
(11)
Проинтегрировав обе части уравнения (11), получим общий интеграл уравнения (10):

Замечание 1. При делении обеих частей уравнения (10) на произведение  могут быть потеряны частные решения, обращающие в нуль произведение
могут быть потеряны частные решения, обращающие в нуль произведение  .
.
Замечание 2. Уравнение с разделенными переменными (8) является частным случаем уравнения с разделяющимися переменными.
Пример 3.Решить уравнение 
Решение. Так как  , то получим
, то получим

Это уравнение с разделяющимися переменными.
Разделив это уравнение на  и умножив его на
и умножив его на 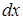 , получим
, получим

Интегрируя, получим
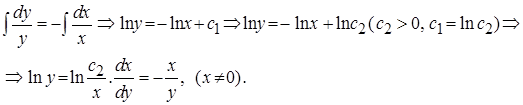
Откуда 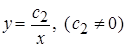 - общее решение нашего уравнения в общем виде.
- общее решение нашего уравнения в общем виде.
При делении обеих частей уравнения на  можно потерять решение
можно потерять решение
 . Оно также является особым (или частным) решением уравнения. Заметим, что это решение можно получить из общего при
. Оно также является особым (или частным) решением уравнения. Заметим, что это решение можно получить из общего при  . Поэтому в ответе достаточно указать
. Поэтому в ответе достаточно указать 
Пример 4.Решить уравнение

Решение. Представим уравнение в виде
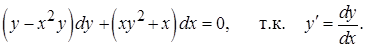
Вынесем общие множители за скобки

Это уравнение с разделяющимися переменными. Перенесем второе слагаемое в правую сторону

Разделим обе части уравнения на произведение

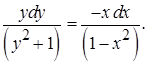
Интегрируя обе части уравнения, найдем общее решение

Умножим обе части уравнения на 2
- общее решение (общий интеграл) уравнения в неявном виде. При делении обеих частей уравнения на произведение могли потерять решение ,…Уравнения вида
где и с - постоянные числа , приводятся к уравнениям с разделяющимися переменными с помощью подстановки Замечание 1. Если с = 0, получим уравнениеОднородные уравнения
(14) Пример 6. Является ли функция однородной? Решение. Проверим на однородность функцию , используя условие (14):Решение.
Данная функция является однородной степени m = 1. Определение. Дифференциальное уравнение первого порядкаЛинейные дифференциальные уравнения первого порядка
Определение. Линейными дифференциальными уравнениями первого порядка называются уравнения, линейные относительно неизвестной функции и её… Линейное дифференциальное уравнение имеет вид: (20)Решение линейного уравнения методом подстановки
Подставим у и у' в уравнение (20): (22)Преобразованное уравнение (26) является линейным относительно и .
Решив его, найдем общий интеграл уравнения (26).
Далее, подставив , получим общее решение уравнения Бернулли (24).
Пример 14. Решить задачу КошиНахождение общего решения уравнения
Если выполняется условие (29), то уравнение (27) может быть записано в виде Тогда общий интеграл этого уравнения имеет видIII. Числовые ряды
Если каждому натуральному числу поставлено в соответствие некоторое вполне определенное число , то говорят, что задана числовая последовательность.
Число называют -м членом последовательности, а формулу - формулой общего члена… Числовую последовательность можно рассматривать как числовую функцию, определенную на множестве натуральных чисел.Интегральный признак Коши
Пример 18. Исследовать на сходимость обобщенный гармонический рядСледовательно, обобщенный гармонический ряд сходится при и расходится при .
2. Признак Даламбера (Д ‘Аламбера) Пусть для ряда существует предел (36)Признак сравнения
1) из сходимости ряда следует сходимость ряда ; 2) из расходимости ряда следует расходимость ряда .Предельный признак сравнения
При использовании признаков сравнения (3, 4) в каждом конкретном случае необходимо найти соответствующий вспомогательный ряд, про который точно… 1) Обобщенный гармонический ряд сходится при и расходится при ; 2) Ряд, из элементов геометрической прогрессии сходящийся при и расходящийся при .Предельный признак Коши
Пусть для ряда существует предел
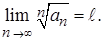 (37)
(37)
Тогда
1) при l < 1 ряд 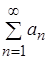 сходится;
сходится;
2) при l > 1 ряд 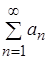 расходится;
расходится;
3) при l = 1 вопрос о сходимости данного ряда остается открытым.
Пример 21. Исследовать сходимость ряда

Решение. Общий член данного ряда имеет вид  .
.
Найдем
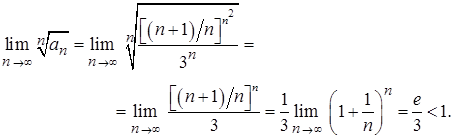
Следовательно, ряд сходится.
В этом примере был использован второй замечательный предел

Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными. Частным случаем знакопеременных рядов являются знакочередующиеся ряды, т. е. такие ряды, все члены которых поочередно меняют знак.
Знакочередующийся ряд может быть записан так
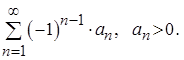 (38)
(38)
Пусть дан знакопеременный ряд  Тогда ряд, составленный из модулей членов данного ряда
Тогда ряд, составленный из модулей членов данного ряда 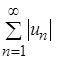 , является знакоположительным рядом.
, является знакоположительным рядом.
Теорема. Если сходится ряд 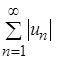 , то сходится и ряд
, то сходится и ряд 
Для знакочередующегося ряда  имеет место следующая теорема (признак Лейбница):
имеет место следующая теорема (признак Лейбница):
Если члены знакочередующегося ряда (38) удовлетворяют условиям:
1)  2)
2) 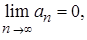
то ряд сходится, а его сумма S не превосходит первого члена, т.е.  .
.
Определение. Если сходится ряд 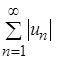 , то ряд
, то ряд  называется абсолютно сходящимся. Если ряд
называется абсолютно сходящимся. Если ряд  сходится, а ряд
сходится, а ряд 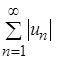 расходится, то ряд
расходится, то ряд  называется условно сходящимся.
называется условно сходящимся.
Исследование знакочередующегося ряда на сходимость начинают с проверки на абсолютную сходимость. Если ряд, составленный из модулей членов ряда, расходится, применяют признак Лейбница.
Пример 22. Исследовать на сходимость ряд 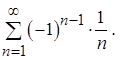
Решение. Составим ряд из модулей 
Получим гармонический ряд, который расходится. Проверим условия признака Лейбница:
1) 
2) 
Оба условия выполняются, следовательно, ряд сходится условно.
IV. Функциональные ряды
Определение. Ряд вида (39) членами которого являются функции называется функциональным.V. Степенные ряды
(40) где - действительные числа, принадлежит некоторому интервалу. Числа называются коэффициентами степенного ряда.Решение.
а) 
Для нахождения интервала сходимости воспользуемся признаком Коши и вычислим предел
Ряд сходится, если , т.е. Решая полученное равенство, найдем интервал сходимости ряда:Найдем радиус сходимости данного ряда, для этого воспользуемся формулой
Тогда Интервал сходимости ряда найдем, решив равенство:Ряды Тейлора и Маклорена
(42) 0! = 1, n! = 1×2×3×4× ××× ×n,… Такой ряд называется рядом Тейлора функции в точке .Методы разложения функций в ряд Тейлора
Отметим, что для любой элементарной функции существуют числа , такие, что в интервале она разлагается в ряд Тейлора. Рассмотрим некоторые методы разложения функций в ряд Тейлора на примерах. Пример 24.Решение. Воспользуемся формулой суммы бесконечно убывающей геометрической прогрессии
где - первый член прогрессии, - знаменатель прогрессии. Тогда приДанное разложение имеет место для всех .
Варианты заданий для контрольной работы № 6
Задание 1. Решить дифференциальные уравнения
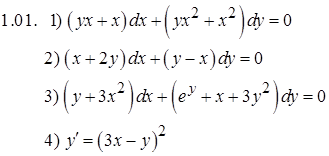

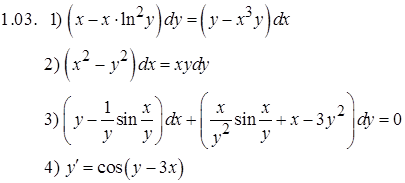
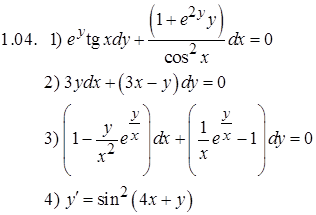
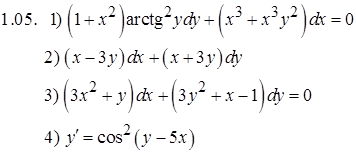
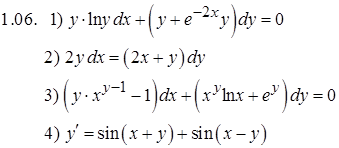
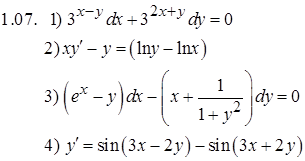
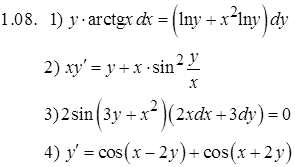

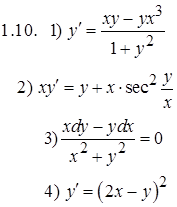

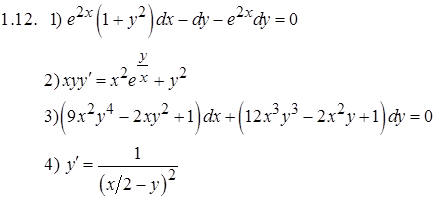








Задание 2. Решить задачу Коши
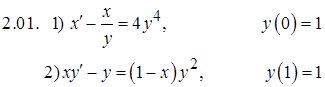
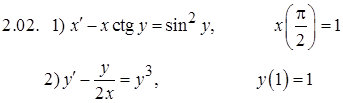


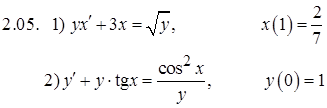

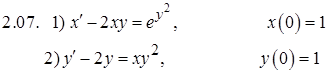



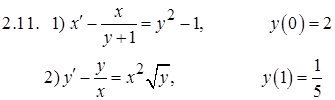




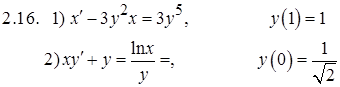
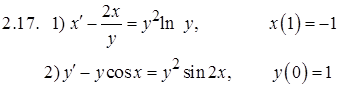
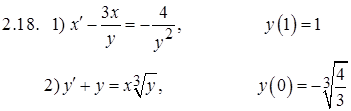


Задание 3. Исследовать на сходимость числовые ряды




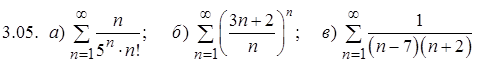







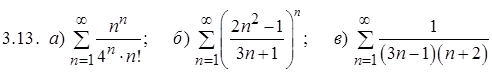




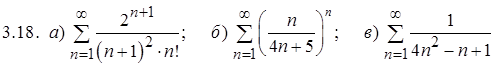

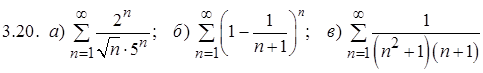 .
.
Задание 4. Найти интервал и радиус сходимости степенного ряда
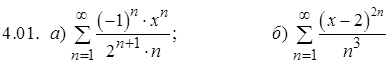
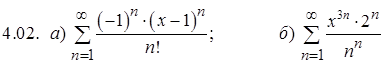
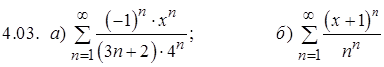
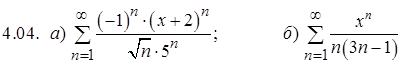




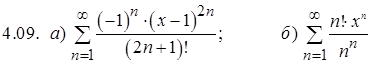


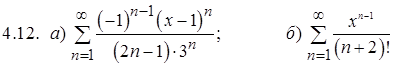







 .
.
Задание 5. Разложить данную функцию в ряд Тейлора в данной точке

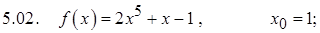








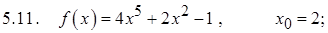






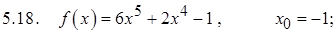
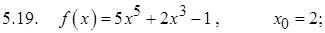

Задание 6. Разложить в ряд Маклорена, используя известные разложения
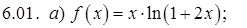
 .
.


 .
.
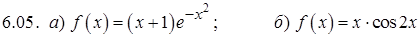 .
.
 .
.
 .
.
 .
.
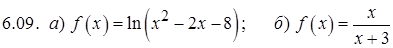 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
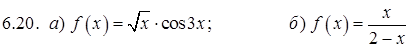 .
.
УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Литература обязательная
1. Пискунов Н. С. Дифференциальное и интегральное исчисление для втузов. Т. 1, Т. 2. – М.: Наука, 1985. – 450 с.
2. Бермант А. Ф., Араманович И. Г. Краткий курс математического анализа. – М.: Наука, 1973. – 436 с.
3. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980. – 432 с.
4. Берман Г. Н. Сборник задач по курсу математического анализа. – М: Наука, 1977 (и позднее).
5. Кудрявцев Л. Д. Курс математического анализа. Т. 1. – М: Высшая школа, 1981. – 687 с.
6. Высшая математика в упражнениях и задачах. Части I, II /
П. К. Данко и др. – М.: Высшая школа, 1980.
7. Марон И. А. Дифференциальное и интегральное исчисление в примерах и задачах. Функции одной переменной. – М.: Наука, 1973.
8. Задачи и упражнения по математическому анализу / под ред.
Б. П. Демидовича. – М.: Наука, 1972.
9. Ефремова О. Н., Столярова Г. П., Некряч Е. Н. Высшая математика. Ч. II: учебное пособие. – Томск: Изд-во ТПУ, 2007. – 200 с.
10. Арефьев К. П. , Глазырина Е. Д., Ефремова О. Н., Столярова Г. П. Высшая математика. Ч. III.: учебное пособие. - Томск: Изд-во ТПУ, 2006. – 208 с.
11. Кошельская Г. А., Столярова Г. П., Харлова А. Н. Высшая математика. Часть IV. Ряды: учебное пособие. - Томск. Изд. ТПУ, 2001.
12. Нагорнова А. И., Столярова Г. П. Высшая математика. Часть III: Рабочая тетрадь к типовому расчету «Неопределенный интеграл» для студентов технических специальностей института дистанционного образования. – Томск: Изд. ТПУ, 2000.
13. Кан Ен Хи, Пестова Н. Ф., Подскребко Э. Н. Дифференциальное исчисление функций одной переменной: учебное пособие. – Томск: ТПУ, 1999.
14. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Т. 2. - М.: Высшая школа, 1989.
– Конец работы –
Используемые теги: Матанализ0.037
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МАТАНАЛИЗ 3
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов