Далее, подставив , получим общее решение уравнения Бернулли (24).
Замечание. При интегрировании уравнений Бернулли можно сразу применить подстановку  , не преобразовывая их в линейные.
, не преобразовывая их в линейные.
Пример 14. Решить задачу Коши
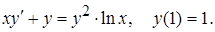
Решение. Разделим уравнение на 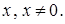

Получим уравнение Бернулли, т. к. в правую часть входит у и у', 
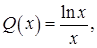
 .
.
Решение ищем в виде:
 (см. Замечание),
(см. Замечание),

Подставим  и
и 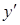 в уравнение
в уравнение  получим
получим
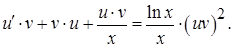
Вынесем за скобки u в первой степени
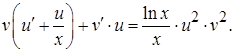
Полагая, что 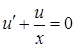 , имеем
, имеем 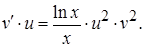
Запишем систему уравнений

Решая первое уравнение системы, найдем его частное решение.

Подставим  во второе уравнение системы и найдем её общее решение.
во второе уравнение системы и найдем её общее решение.

Интегрируя левую часть уравнения, получаем
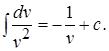
Интеграл, стоящий в правой части равенства, найдем с помощью формулы интегрирования по частям 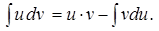
Вычислим:


Окончательно получим

Умножим последнее равенство на (-1) и выразим из него функцию  .
.

Тогда общий интеграл уравнения Бернулли имеет вид:

Воспользуемся начальными условиями у(1) = 1 и найдем  .
.

Подставив с = 0 в общее решение уравнения, найдем его частное решение:

6. Уравнение в полных дифференциалах
Определение. Дифференциальное уравнение первого порядка вида
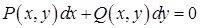 (27)
(27)
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции 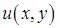 , то есть
, то есть

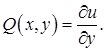 (28)
(28)
Для того чтобы уравнение (27) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие
 (29)
(29)