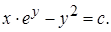Нахождение общего решения уравнения
Если выполняется условие (29), то уравнение (27) может быть записано в виде

Тогда общий интеграл этого уравнения имеет вид
 (30)
(30)
где  - произвольная постоянная.
- произвольная постоянная.
Функция 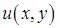 может быть найдена, используя уравнения (28).
может быть найдена, используя уравнения (28).
Интегрируя равенство  по
по 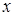 при фиксированном
при фиксированном  и учитывая, что произвольная постоянная в этом случае может зависеть от
и учитывая, что произвольная постоянная в этом случае может зависеть от  , получим
, получим
 (31)
(31)
Затем, дифференцируя найденную функцию  по
по  и подставляя её в равенство
и подставляя её в равенство  , найдем
, найдем  .
.
Подставим функцию  в уравнение (31), получим
в уравнение (31), получим 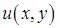 , которая является общим интегралом уравнения (27) с точностью до произвольной постоянной.
, которая является общим интегралом уравнения (27) с точностью до произвольной постоянной.
Замечание. Для нахождения общего решения уравнения (27) можно было начать с интегрирования равенства  при фиксированном
при фиксированном 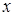 . Тогда постоянная интегрирования может зависеть от
. Тогда постоянная интегрирования может зависеть от 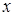 .
.
Пример 15. Решить уравнение 
Решение. 
Проверим условие (29): 
Следовательно, левая часть уравнения есть полный дифференциал некоторой функции 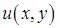 и решение будет иметь вид:
и решение будет иметь вид:
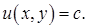
Воспользуемся условиями (28).
Тогда 
Проинтегрируем первое соотношение по х:
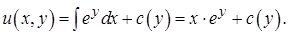
Затем продифференцируем  по
по  :
:

Так как  , то получим
, то получим

Отсюда 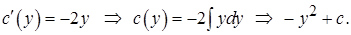
Пусть 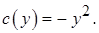
Тогда  и общий интеграл уравнения имеет вид
и общий интеграл уравнения имеет вид