IV. Функциональные ряды
Пусть  последовательность функций, определенных на некотором множестве Х.
последовательность функций, определенных на некотором множестве Х.
Определение. Ряд вида
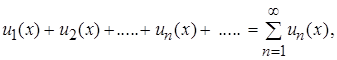 (39)
(39)
членами которого являются функции 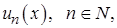 называется функциональным.
называется функциональным.
Каждому значению 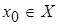 соответствует числовой ряд
соответствует числовой ряд 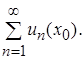 Он может быть как сходящимся, так и расходящимся. Если ряд
Он может быть как сходящимся, так и расходящимся. Если ряд 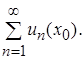 сходится, точка
сходится, точка  называется точкой сходимости функционального ряда (39).
называется точкой сходимости функционального ряда (39).
Множество 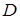 всех точек сходимости функционального ряда называется его областью сходимости. Сходимость функционального ряда в каждой точке
всех точек сходимости функционального ряда называется его областью сходимости. Сходимость функционального ряда в каждой точке 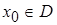 называется поточечной сходимостью.
называется поточечной сходимостью.
Определение. Функциональный ряд (39) называется равномерно сходящимся в области 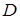 к функции
к функции  , если для любого
, если для любого  существует номер
существует номер  , не зависящий от
, не зависящий от 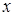 , такой, что
, такой, что
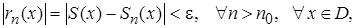
где  n-я частичная сумма ряда,
n-я частичная сумма ряда,  сумма ряда.
сумма ряда.
Теорема (признак Вейерштрасса). Если члены ряда  удовлетворяют неравенствам
удовлетворяют неравенствам 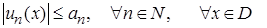 и ряд
и ряд  сходится, то функциональный ряд
сходится, то функциональный ряд  сходится равномерно в области
сходится равномерно в области 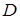 .
.
Числовой ряд 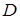
 , члены которого удовлетворяют неравенствам теоремы, называется мажорантой (мажорантным рядом) для функционального ряда
, члены которого удовлетворяют неравенствам теоремы, называется мажорантой (мажорантным рядом) для функционального ряда  , а сам функциональный ряд называется в этом случае мажорируемым на множестве
, а сам функциональный ряд называется в этом случае мажорируемым на множестве 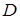 .Из признака Вейерштрасса следует, что условие мажорируемости ряда является достаточным для его равномерной сходимости.
.Из признака Вейерштрасса следует, что условие мажорируемости ряда является достаточным для его равномерной сходимости.
Сформулируем свойства равномерно сходящихся рядов:
1. (О непрерывности суммы функционального ряда)
Если на множестве 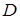 функциональный ряд (39) с непрерывными членами сходится равномерно, то его сумма
функциональный ряд (39) с непрерывными членами сходится равномерно, то его сумма  непрерывна на
непрерывна на 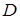 .
.
2. (О почленном интегрировании)
Если функциональный ряд (39) с непрерывными членами сходится к функции  равномерно на отрезке
равномерно на отрезке 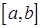 , то его можно почленно интегрировать на любом отрезке
, то его можно почленно интегрировать на любом отрезке  , и справедливо неравенство:
, и справедливо неравенство:
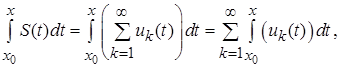
причем ряд  сходится равномерно на отрезке
сходится равномерно на отрезке 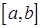 .
.
3. (О почленном дифференцировании)
Если функциональный ряд (39) с непрерывно дифференцируемыми на отрезке 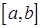 членами сходится к функции
членами сходится к функции  , а ряд
, а ряд  сходится равномерно на
сходится равномерно на 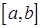 , то ряд (39) сходится равномерно на
, то ряд (39) сходится равномерно на 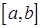 , его сумма
, его сумма  - непрерывно дифференцируемая функция, и справедливо неравенство:
- непрерывно дифференцируемая функция, и справедливо неравенство:
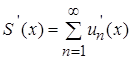 .
.