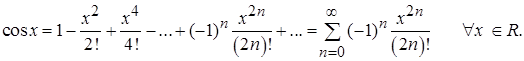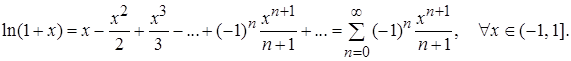Ряды Тейлора и Маклорена

Рассмотрим некоторую функцию 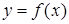, определенную на интервале , и пусть . Допустим также, что функция 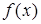имеет в окрестности точки производные любого порядка. Поставим функции 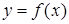в соответствие степенной ряд, (окрестностью точки называется любой интервал, содержащий эту точку ),

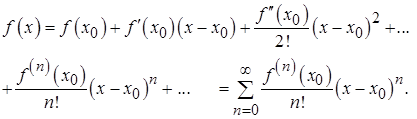(42)

0! = 1, n! = 1×2×3×4× _××× ×n, n Î N .

Такой ряд называется рядом Тейлора функции 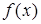в точке .

Если 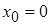, то ряд Тейлор имеет вид:

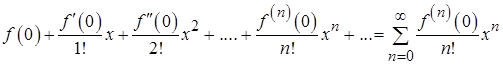(43)

и называется рядом Маклорена.

Радиус сходимости ряда Тейлора может быть равен нулю или отличен от нуля. Причем, в последнем случае сумма ряда Тейлора может не совпадать с функцией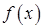. Если ряд Тейлора сходится к функции 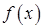, для которой он составлен, то говорят, что 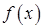разложима в ряд Тейлора в окрестности точки .

Заметим, что частичные суммы ряда Тейлора

представляют собой многочлены Тейлора функции 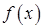в точке . Если ряд сходится к функции 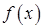, справедливо равенство

где - многочлен Тейлора, - остаточный член формулы Тейлора.

Напомним, что остаточный член формулы Тейлора может быть записан в одном из следующих видов:

- форма Лагранжа,

- форма Коши.

Имеет место необходимый и достаточный признак разложимости функции в ряд Тейлора.

Теорема 1.Для того, чтобы существовало разложение в ряд Тейлора бесконечно дифференцируемой в окрестности точки функции 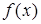необходимо и достаточно, чтобы

где - остаточный член формулы Тейлора,

Теорема 2. (Достаточный признак разложимости функции в ряд Тейлора). Если для все производные функции 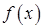, ограничены одной и той же константой М, то ряд Тейлора сходится к функции 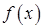в интервале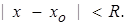

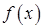Теорема 3.Если степенной ряд по степеням сходится к функции в окрестности точки , то он является рядом Тейлора функции 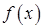в окрестности этой точки.

Приведем примеры разложения в ряд Маклорена основных элементарных функций: