Коэффициент запаса, допускаемое напряжение
Расчёт на прочность и жёсткость осуществляется двумя методами: методом допускаемых напряжений, деформаций и методом допускаемых нагрузок.
Напряжения 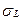 , при которых образец из данного материала разрушается или при которых развиваются значительные пластические деформации, называются предельными. Эти напряжения зависят от свойств материала и вида деформации.
, при которых образец из данного материала разрушается или при которых развиваются значительные пластические деформации, называются предельными. Эти напряжения зависят от свойств материала и вида деформации.
Напряжение 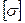 , величина которого регламентируется техническими условиями, называется допускаемым.
, величина которого регламентируется техническими условиями, называется допускаемым.
Допускаемое напряжение – это наибольшее напряжение, при котором обеспечивается требуемая прочность, жёсткость и долговечность элемента конструкции в заданных условиях его эксплуатации.
Допускаемое напряжение составляет некоторую долю от предельного напряжения:
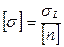 , (2.18)
, (2.18)
где 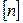 – нормативный коэффициент запаса, число, показывающее, во сколько раз допускаемое напряжение меньше предельного.
– нормативный коэффициент запаса, число, показывающее, во сколько раз допускаемое напряжение меньше предельного.
Для пластичных материалов допускаемое напряжение выбирают так, чтобы при любых неточностях расчёта или непредвиденных условиях эксплуатации в материале не возникло остаточных деформаций, т. е. 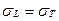 (предел текучести):
(предел текучести):

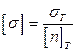 , (2.19)
, (2.19)
где 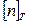 – коэффициент запаса прочности по отношению к
– коэффициент запаса прочности по отношению к 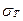 .
.
Для хрупких материалов допускаемые напряжения назначаются из условия, что материал не разрушится, т. е 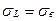 (предел прочности):
(предел прочности):
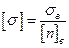 , (2.20)
, (2.20)
где 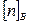 – коэффициент запаса прочности по отношению к
– коэффициент запаса прочности по отношению к 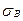 .
.
В машиностроении (при статическом нагружении) коэффициенты запаса прочности принимают: для пластичных материалов 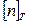 =1,4 – 1,8; для хрупких –
=1,4 – 1,8; для хрупких – 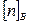 =2,5 – 3,0.
=2,5 – 3,0.
Расчёт на прочность по допускаемым напряжениям основан на том, что наибольшее расчётное напряжение в опасном сечении стержневой конструкции не превосходит допускаемого значения (меньше – не более 10 %, больше – не более 5 %):
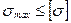 . (2.21)
. (2.21)
Оценка жёсткости стержневой конструкции проводится на основе проверки условия жёсткости при растяжении:
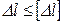 . (2.22)
. (2.22)
Величина допускаемой абсолютной деформации [∆l] назначается отдельно для каждой конструкции.
Метод допускаемых нагрузок заключается в том, что внутренние силы, возникающие в наиболее опасном сечении конструкции в процессе эксплуатации, не должны превышать допускаемых значений нагрузок:
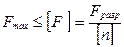 , (2.23)
, (2.23)
где 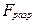 - разрушающая нагрузка, полученная в результате расчётов или экспериментов с учётом опыта изготовления и эксплуатации;
- разрушающая нагрузка, полученная в результате расчётов или экспериментов с учётом опыта изготовления и эксплуатации;
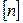 – коэффициент запаса прочности.
– коэффициент запаса прочности.
В дальнейшем будем использовать метод допускаемых напряжений и деформаций.
2.6. Проверочный и проектировочный расчёты
на прочность и жёсткость
Условие прочности (2.21) даёт возможность проводить три вида расчетов:
– проверочный – по известным размерам и материалу стержневого элемента (заданы площадь сечения А и [σ]) проверить, в состоянии ли он выдержать заданную нагрузку (N):
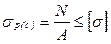 ; (2.24)
; (2.24)
– проектировочный – по известным нагрузкам (N – задано) и материалу элемента, т. е. по известному [σ], подобрать необходимые размеры поперечного сечения, обеспечивающего его безопасную работу:
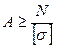 ; (2.25)
; (2.25)
– определение допускаемой внешней нагрузки – по известным размерам (А – задано) и материалу элемента конструкции, т. е. по известному [σ], найти допускаемую величину внешней нагрузки:
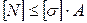 . (2.26)
. (2.26)
Оценка жёсткости стержневой конструкции проводится на основе проверки условия жёсткости (2.22) и формулы (2.10) при растяжении:
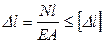 . (2.27)
. (2.27)
Величина допускаемой абсолютной деформации [∆l] назначается отдельно для каждой конструкции.
Аналогично расчётам по условию прочности условие жёсткости также предполагает три вида расчётов:
– проверка жёсткости данного элемента конструкции, т. е. проверка выполнения условия (2.22);
– расчёт проектируемого стержня, т. е. подбор его поперечного сечения:
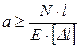 ; (2.28)
; (2.28)
– установка работоспособности данного стержня, т. е. определение допустимой нагрузки:
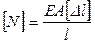 . (2.29)
. (2.29)
Прочностной анализ любой конструкции содержит следующие основные этапы:
1. Определение всех внешних сил и сил реакций опор.
2. Построение графиков (эпюр) силовых факторов, действующих в поперечных сечениях по длине стержня.
3. Построение графиков (эпюр) напряжений вдоль оси конструкции, нахождение максимума напряжений. Проверка условий прочности в местах максимальных значений напряжений.
4. Построение графика (эпюры) деформации стержневой конструкции, нахождение максимумов деформации. Проверка в сечениях условий жёсткости.
 |
Пример 2.1. Для стального стержня, изображённого на рис. 9а, определить во всех поперечных сечениях продольную силу N и напряжение σ. Определить также вертикальные перемещения δ для всех поперечных сечений стержня. Результаты изобразить графически, построив эпюры N, σ и δ. Известно: F1 = 10 кН; F2 = 40 кН; А1 = 1 см2; А2 = 2 см2; l1 = 2 м; l2 = 1 м.
Решение. Для определения N, используя метод РОЗУ, мысленно разрезаем стержень по сечениям I−I и II−II. Из условия равновесия части стержня ниже сечения I−I (рис. 9.б) получим 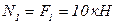 (растяжение). Из условия равновесия стержня ниже сечения II−II (рис. 9в) получим
(растяжение). Из условия равновесия стержня ниже сечения II−II (рис. 9в) получим
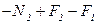 ,
,
откуда 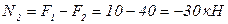 (сжатие). Выбрав масштаб, строим эпюру продольных сил (рис. 9г). При этом растягивающую силу
(сжатие). Выбрав масштаб, строим эпюру продольных сил (рис. 9г). При этом растягивающую силу 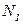 считаем положительной, сжимающую
считаем положительной, сжимающую 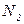 − отрицательной.
− отрицательной.
Напряжения равны: в сечениях нижней части стержня (рис. 9б)
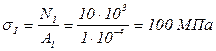 (растяжение);
(растяжение);
в сечениях верхней части стержня
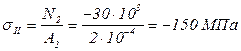 (сжатие).
(сжатие).
В выбранном масштабе строим эпюру напряжений (рис. 9д).
Для построения эпюры δ определяем перемещения характерных сечений В−В и С−С (перемещение сечения А−А равно нулю).
Сечение В−В будет перемещаться вверх, поскольку верхняя часть сжимается:
 (вверх).
(вверх).
Перемещение сечения, вызванное растяжением, считается положительным, вызванное сжатием – отрицательным.
Перемещение сечения С−С является алгебраической суммой перемещений В−В (δВ) и удлинения части стержня длиной l1:
 .
.
В определённом масштабе откладываем значения 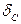 и
и 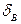 , соединяем полученные точки прямыми линиями, так как при действии сосредоточенных внешних сил перемещения линейно зависят от абсцисс сечений стержня, и получаем график (эпюру) перемещений (рис. 9е). Из эпюры видно, что некоторое сечение D–D не перемещается. Сечения, расположенные выше сечения D–D , перемещаются вверх (стержень сжимается); сечения, расположенные ниже, перемещаются вниз (стержень растягивается).
, соединяем полученные точки прямыми линиями, так как при действии сосредоточенных внешних сил перемещения линейно зависят от абсцисс сечений стержня, и получаем график (эпюру) перемещений (рис. 9е). Из эпюры видно, что некоторое сечение D–D не перемещается. Сечения, расположенные выше сечения D–D , перемещаются вверх (стержень сжимается); сечения, расположенные ниже, перемещаются вниз (стержень растягивается).