Геометрические характеристики некоторых сечений

 

Рассмотрим геометрические характеристики наиболее часто встречающихся форм сечений элементов конструкций.

 

3.4.1. Сечение в форме прямоугольника

 

Пусть сечение имеет форму прямоугольника со сторонами bxh (рис. 14).

Выберем произвольную систему координат xOy (совместив её со сторонами прямоугольника); выделим на расстоянии у от оси x элементарную площадку dA = b∙dy. Тогда по определению (формула 3.1) получим:

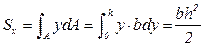. (3.18)

Аналогично определяется статический момент сечения относительно оси y:

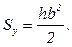(3.19)

Используя формулы (3.2), находим координаты центра тяжести прямоугольника в выбранной системе координат:

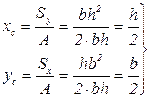, (3.20)

т. е. центр тяжести прямоугольника лежит на пересечении диагоналей.

Для определения осевого момента инерции 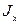сечения относительно оси х воспользуемся формулой (3.6.):

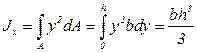. (3.21)

Аналогично находим осевой момент инерции сечения относительно оси у: 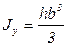. (3.22)

Используя формулы (3.10), найдём осевые моменты инерции прямоугольного сечения относительно центральных осей:

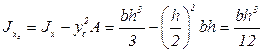. (3.23)

По аналогии находим 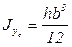. (3.24)

Моменты сопротивления площади сечения данной фигуры найдём, используя формулу (3.14):

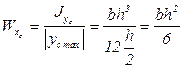; (3.25)

аналогично находим 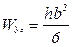. (3.26)

3.4.2. Сечение в форме полукруга и круга

Определим центр тяжести сечения, имеющего форму полукруга с радиусом r (рис. 15). Так как ось y является осью симметрии полукруга, то центр C тяжести сечения лежит на оси y, т. е. x_c = 0.

Для определения ординаты y_c используем выражение (3.1):

 

,

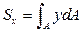где А – площадь полукруга. Из рис. 16 видно, что площадь элементарной площадки

,

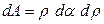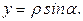
Подставляя значения dA и y в исходную формулу, получим:

 

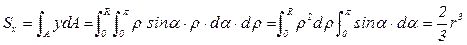. (3.27)

Положение центра тяжести полукруга находим по формуле (3.2):

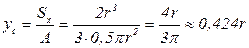. (3.28)

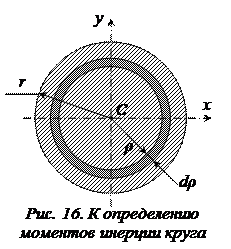
Для определения полярных моментов инерции круглого сечения (рис. 16) выделим из круга элементарное кольцо толщиной 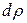радиусом и площадью 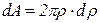. Полярный момент инерции элементарного кольца относительно центра круга С

.

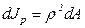Подставляя значение dA и интегрируя, получим

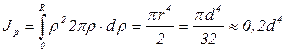. (3.29)

Учитывая (3.9) и (3.17), находим

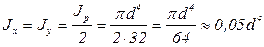. (3.30)

Учитывая (3.14) и (3.16), найдём моменты сопротивления изгибу и кручению сечения круглой формы:

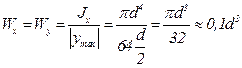; (3.31)

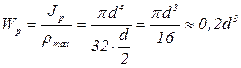. (3.32)