Уравнение упругой линии балки

 

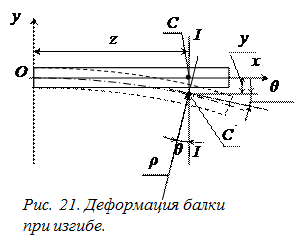Изогнутая ось, представляющая собой геометрическое место центров тяжести поперечных сечений деформированного бруса, называется упругой линией. В результате прогиба балки центр тяжести С (рис. 21) каждого поперечного сечения I−I получает вертикальное и горизонтальное перемещения, а само сечение поворачивается на некоторый угол θ вокруг своей нейтральной оси.

На основании гипотезы малых деформаций в сопротивлении материалов при изгибе балок горизонтальные перемещения считаются ничтожно малыми по сравнению с вертикальными и не учитываются. Вертикальные же перемещения y являются основным определяющим фактором, их обычно называют прогибами.

В инженерной практике большое значение имеет оценка прогибов и сопоставление их наибольших значений с допускаемыми, определяемыми условиями работы балки, т. е. расчёт балок на жёсткость.

Существует несколько методов определения перемещений: с помощью дифференциального уравнения упругой линии балки, метод начальных параметров, энергетический, интеграл Мора, использование правила Верещагина.

Определим перемещение с помощью дифференциального уравнения упругой линии балки. Опираясь на гипотезу малости деформации, можно считать, что 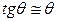(рис.21) и, следовательно,

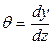. (4.17)

Из аналитической геометрии известно, что радиус кривизны ρ кривой у = y(z) выражается как

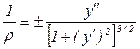. (4.18)

Ввиду малости деформаций (y' = dy/dz << 1) выражение (5.19) упрощается:

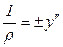. (4.19)

Подставляя в (4.19) значение (4.9), получим дифференциальное уравнение упругой линии или дифференциальное уравнение изгиба балки в виде:

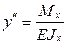. (4.20)

Здесь учтено, что положительный изгибающий момент (сжатые волокна сверху) соответствует положительной кривизне балки. Значения прогибов балки получаются, таким образом, двукратным интегрированием уравнения (4.20). В уравнении (4.20) под М_х следует понимать его аналитическое выражение как функцию от координаты z–.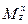

Проинтегрировав один раз уравнение (4.20), получим зависимость углов наклона касательных к упругой линии θ, равных углам поворота поперечных сечений.

В результате второго интегрирования получаем уравнение упругой линии балки (уравнение прогибов).

Следует отметить, что если балка имеет несколько участков нагружения, то определение её упругой линии непосредственным интегрированием дифференциального уравнения (4.20) становится сложным из-за необходимости нахождения большого числа постоянных интегрирования из граничных условий. Поэтому в общем случае нагружения балок упругую линию, как правило, ищут другими методами, где упрощено нахождение постоянных интегрирования.

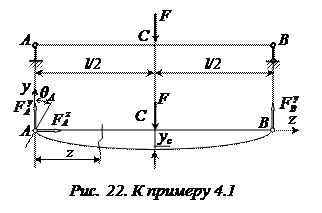Пример 4.1. Определить прогиб 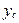посередине пролёта балки и угол 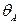поворота поперечного сечения на левой опоре. Жёсткость балки на изгиб – EJ_x, длина балки – l (рис. 22).

Решение. Для определения перемещений необходимо составить выражения для изгибающего момента на участке АС. Для этого определим опорные реакции. В нашем случае

.

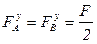Тогда аналитическое выражение для изгибающего момента 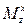на участке АС в сечении с координатой z (рис.22):

.

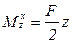Уравнение (4.20) для нашего случая запишется в виде:

.

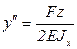Интегрируя один раз, получим выражение для угла поворота поперечных сечений:

,

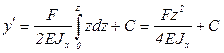где С – постоянная интегрирования, определяемая из граничных условий (в нашем случае граничными условиями являются: при ):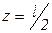

.

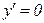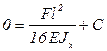Откуда находим значение С:

.

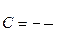
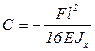Таким образом,

.

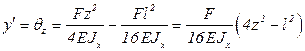Подставляя значение z = 0, найдём угол поворота сечения 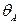балки в опоре А:

.

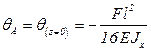Интегрируя полученное выражение для 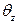, определим прогибы балки :

.

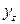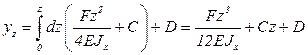Постоянную интегрирования D найдём из условия равенства нулю прогиба балки в опоре А при :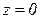

.

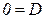Аналитическое выражение для прогиба балки примет вид:

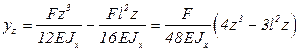
Максимальный прогиб балки будет в точке С при :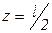

.

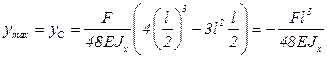Отрицательное значение перемещение точки С означает, что оно не совпадает с направлением оси у.