Вопросы для самопроверки

1. Что называется сдвигом?

2. Что называется абсолютным и относительным сдвигом?

3. Как формулируется закон Гука при сдвиге?

4. Как связаны между собой модуль продольной упругости Е и модуль сдвига G?

5. Как производится расчёт на прочность при сдвиге?

6. Какой вид деформации называют кручением?

7. Чему равен крутящий момент в каком-либо сечении вала?

8. Как определяют наибольший крутящий момент?

9. Как определяют напряжение при кручении?

10. Как определяется угол закручивания вала?

11. Чему равна жёсткость стержня (вала) при кручении и что она характеризует?

6. Напряжённое и деформированное состояние в точке

6.1. Напряжённое состояние в точке

 

Понятие «напряжение в точке» связано как с самой точкой, так и с положением площадки, проведённой через данную точку. Поскольку через точку тела можно провести бесчисленное множество сечений, то в данной точке имеется и бесчисленное множество напряжений, связанных с площадками их действия Совокупность нормальных и касательных напряжений для множества элементарных площадок, проходящих через точку, называется напряжённым состоянием в точке. Сущность метода расчёта на прочность по допускаемым напряжениям состоит в нахождении этих напряжений, определении экстремальных значений и в сравнении их с допускаемым напряжением для материала элемента конструкции.

Вырежем около анализируемой точки D сечения тела элементарный параллелепипед (рис. 28а), оси которого (рис. 28б) ориентированы так же, как и оси х, у, z, по которым раскладывались главный вектор и главный момент внутренних сил в сечении, т. е. грани параллельны координатным плоскостям.

На гранях элементарного параллелепипеда внутренние силы ввиду малости площадок можно считать равномерно распределёнными в пределах каждой грани. По определениям (1.4)–(1.6) внутренние равномерные силы на элементарных гранях считаются напряжениями в точке.

 

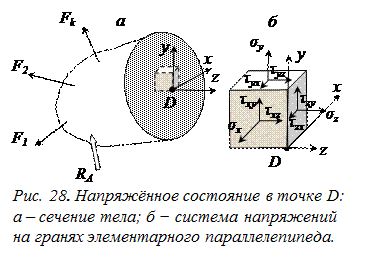Разложив полное напряжение в точке D по осям координат, получим систему напряжений в точке (у касательных напряжениях первый индекс указывает ось, перпендикулярно которой расположена площадка; второй − ось, параллельно которой действует напряжение σ_x, σ_y, σ_z, τ_ху, τ_ух, τ_zx, τ_xz, τ_yz, τ_zy). При изменении ориентации параллелепипеда около выбранной точки D (например, поворота) по его граням будет действовать другая система напряжений, значения которых могут быть определены через старые.

Так как мысленно вырезанный из тела параллелепипед, по предположению, находится в равновесии под действием системы напряжений в точке, то суммы проекций всех сил на оси координат и суммы моментов всех сил относительно координатных осей должны быть равны нулю. Из этого следует:

– нормальные напряжения на противоположных гранях равны и противоположно направлены;

– на взаимно перпендикулярных площадках координатные составляющие касательных напряжения равны и направлены либо к смежному ребру, либо от него. Это положение носит название закона парности касательных напряжений.

Среди бесчисленного множества площадок, проходящих через рассматриваемую точку, имеется, по меньшей мере, три взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения. Такие площадки называются главными. Нормальные напряжения на главных площадках называются главными и обозначаются 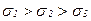с учётом знаков (после определения численных значений).

Если отличны от нуля все три главных напряжения, то такое напряжённое состояние называется трёхосным или объёмным.

Если одно из главных напряжений равно нулю, то такое напряжённое состояние называется двухосным или плоским.

Если равны нулю два главных напряжения, то напряжённое состояние – одноосное или линейное.

Зная напряжённое состояние в любой точке детали, можно оценить прочность самой детали.

 

6.2. Напряжённое состояние при растяжении (сжатии)

 

Для того чтобы иметь представление о прочности материала, необходимо знать действующие напряжения не только в плоскости поперечного сечения, но и по любому наклонному сечению.

Рассмотрим стержень, который находится под действием растягивающей силы 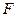(рис. 29). Полагаем, что в поперечных сечениях стержня, достаточно удалённых от точек приложения сосредоточенных сил, нормальные напряжения распределяются равномерно и определяются по формуле (2.3):

.

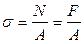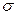В окрестности какой-либо точки S, лежащей в плоскости сечения abb^′a^′ (рис. 29), выделим бесконечно малый элемент (рис. 30а). Поскольку на грани, перпендикулярной к направлению растягивающей силы, действует нормальное напряжение , а на остальных гранях напряжения отсутствуют, то элемент находится в линейном напряжённом состоянии (главные напряжения, 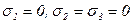). Условимся такой элемент изображать в виде плоской фигуры (рис. 30б), хотя в действительности он имеет форму прямоугольного параллелепипеда.

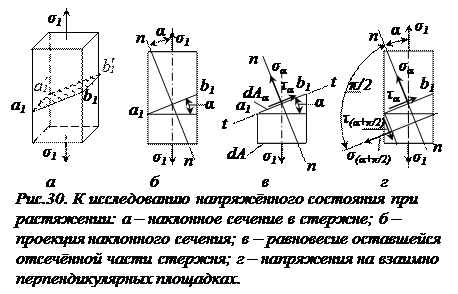Определим напряжение, возникающее в наклонном сечении a₁b₁b₁^′a₁^′(рис. 30а,б), перпендикулярном к плоскости рисунка. Положение наклонной площадки определяется углом α между направлением главного вектора 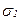и внешней нормалью n−n к площадке. Этот угол считают положительным, если его отсчитывают против часовой стрелки от направления 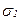. Наклонную площадку обозначают углом, определяющим её положение. Так, для принятого на рис. 6.3б обозначения угла имеем α-площадку (площадка a₁b₁). На этой площадке будут действовать нормальное, σ_α и касательное τ_α напряжения, для определения которых применяют метод сечений. Так как наклонная площадка рассекла элемент на две части, отбросим одну из них (например, верхнюю) и рассмотрим равновесие оставшейся (нижней) части (рис. 30в). Условие равновесия запишем в виде проекций всех сил на нормаль n−n и площадку t−t:

;

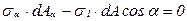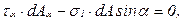
где 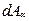– площадь наклонного сечения.

Учитывая, что 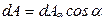, из уравнений равновесия находим:

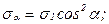(6.1)

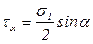. (6.2)

Для определения напряжений на площадке, перпендикулярной к площадке a₁b₁ (рис. 30г), расположенной под углом (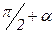), заменим в формулах (6.1) и (6.2) угол α на (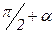), получим:

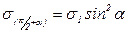; (6.3)

 

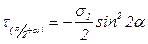. (6.4)

Для направлений напряжений σ и τ, действующих по наклонным площадкам, принимаем следующее правило знаков: нормальное напряжение положительно, если оно растягивающее; касательное напряжение положительно, если для совпадения с его направлением нормаль к площадке необходимо повернуть по направлению движения часовой стрелки.

Отметим некоторые свойства линейного напряжённого состояния, вытекающие из зависимостей (6.1)–(6.4):

1. Сумма нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам, постоянна и равна главному напряжению, т. е.

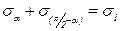. (6.5)

 

Этим свойством нормальных напряжений обычно пользуются для проверки правильности их вычислений.

2. На двух взаимно перпендикулярных площадках касательные напряжения равны, но противоположны по знаку, т. е.

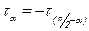. (6.6)

 

Данное свойство является общим для любого напряжённого состояния (закон парности касательных напряжений).

3. Величина нормального напряжения в любом наклонном сечении (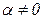) меньше 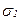и достигает максимума лишь в поперечных сечениях ().

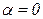4. Касательное напряжение наибольшее значение имеет в сечении, составляющем угол 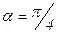с направлением 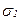. В этом случае

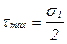. (6.7)

 

Оценивая напряжённое состояние стержня при его осевом растяжении или сжатии, можно сделать заключение о том, что стержень разрушается либо по поперечному сечению в результате действия максимальных нормальных напряжений, либо по наклонной (под углом ) плоскости от действия наибольших касательных напряжений.