Реечное зацепление

Если центр одного из колёс удалить бесконечность, то его окружности преобразятся в параллельные прямые; точка N₁ касания производящей прямой ( она же общая нормаль и

 

Рис.5.8

Рис.5.7

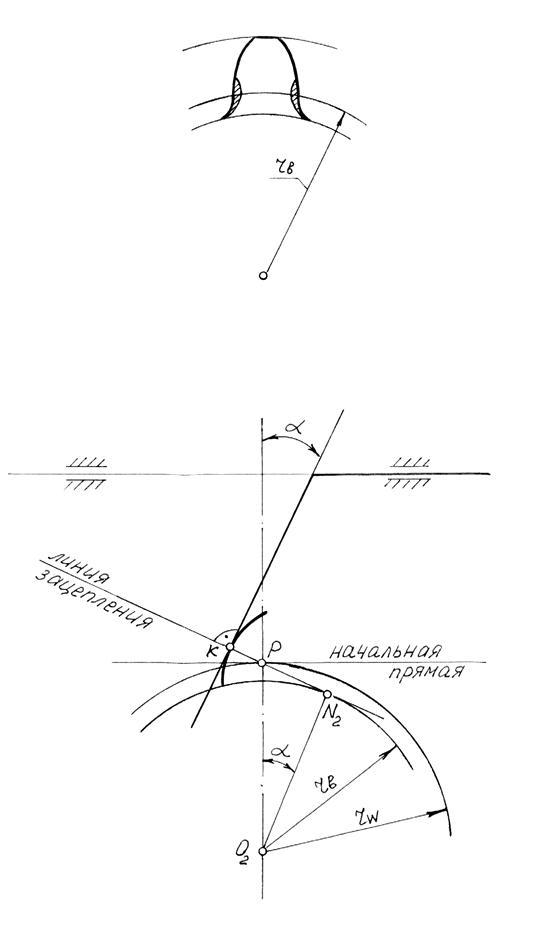
линия зацепления) с основной окружностью тоже удалится в бесконечность в направлении продолжения линии зацепления. Так как радиус кривизны эвольвенты увеличится до бесконечности, то эвольвента (боковой профиль зуба) преобразуется в прямую, перпендикулярную линии зацепления. В результате колесо превратится в рейку, а передача – в реечную передачу, в которой рейка образует со стойкой поступательную пару (рис. 5.8 и 5.9).

5.2.3 Нарезание зубьев колес производящей рейкой

Производящим колесом (рейкой) называется воображаемое колесо (рейка), боковые поверхности зубьев которого образуются режущими кромками инструмента при его движении. Зацепление нарезаемого колеса с производящим колесом (рейкой) называется станочным зацеплением. Так как основным видом инструмента при нарезании колес является инструмент реечного типа, то будем рассматривать нарезание колес производящей рейкой. Контур зубьев производящей рейки называется исходным производящим контуром.

Геометрия зубьев нарезаемого колеса определяется параметрами контуров зубьев производящей рейки и её расположением по отношению к колесу.

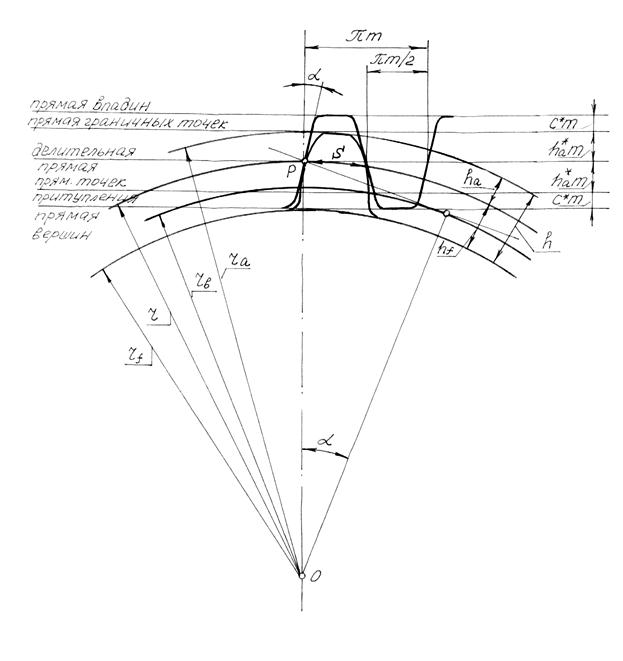
Форма и размеры производящего контура стандартизированы и выражаются в долях модуля m (рис. 5.9). Здесь: a = 20° угол профиля производящего профиля, ha* - коэффициент высоты головки зуба, с* - коэффициент радиального зазора (для колес с нормальной высотой зуба ha* = 1, с*= 0,25), Базой для определения размеров зубьев служит делительная прямая, по которой толщина зуба S равна ширине впадины е

S=е= р/2 = pm / 2 (5.24)

Притупление зубьев рейки у вершины вводится для уменьшения подрезания зубьев нарезаемого колеса, для получения более плавной кривой у их основания, что повышает прочность зубьев нарезаемого колеса.

Колесом без смещения называется колесо, у которого по делительной окружности окружная толщина зуба равна окружной ширине впадины : S=е.

При нарезании колес без смещения делительная окружность колеса катится без скольжения по делительной прямой производящей рейки. Угол профиля зуба колеса в точке на делительной окружности равен углу профиля зуба рейки a и равен углу зацепления.

Основные размеры колеса без смещения.

ha = h_a* m (5.25)

h_f= (h_a* + с*) m (5.26)

da = d+2ha = Zm + 2h_a* m (5.27)

d_f = d - 2h_f = Zm - 2(h_a*+ с* )m (5.28)

h = ha + h_f = (2h_a*+ с* )m (5.29)

 

Рис.5.9

Из треугольника ONP (рис.5.9): ON = OP cos a

или: r_в = r cos a = Zm/2 cos a

Минимальное число зубьев прямзубого колеса, нарезаемого без подрезания, равно

Z_min =17 (при h_a* = 1, С* = 0,25, a = 20°).

Для получения меньших габаритов передачи часто требуется иметь колесо с числом зубьев Z < Z_min.

Для нарезания таких колес без подрезания инструмент смещают на величину Хm (где Х - коэффициент смещения производящего контура). Смещение Хm - это расстояние по нормали между делительной окружностью колеса и делительной прямой рейки; оно считается положительным, если делительная прямая рейки не пересекает делительную окружность колеса (рейка отодвинута от оси колеса).

Смещение вводится не только для устранения подрезания колеса, но и для повышения изгибной и контактной прочности зубьев, для увеличения их износостойкости, а также для вписывания в заданное межосевое расстояние.

Основные размеры колеса со смещением:

h_a = m(h_a* + Х - Dy) (5.30)

h_f = m(h_a* + C* - Х) (5.31)

h = h_a + h_f = m(2 h_a* + C^* - Dy) (5.32)

d_a = d + 2h_a (5.33)

d_f = d - 2h_f (5.34)

Здесь Dy - коэффициент уравнительного смещения (коэффициент уменьшения высоты головки зуба), вводимый для обеспечения в зацеплении стандартного радиального зазора С*m, необходимого для компенсации неточностей изготовления и сборки передачи.

5.3 Косозубая цилиндрическая передача

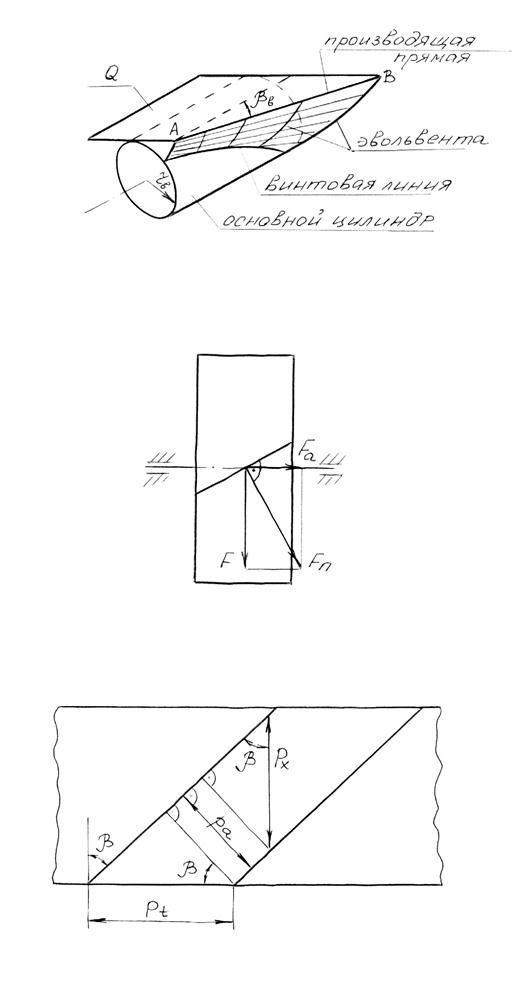
Образование боковой поверхности зуба косозубого колеса можно представить следующим образом (рис.5.10). В плоскости Q под углом b к образующей цилиндра располагается прямая АВ. При перекатывании этой плоскости без скольжения по цилиндру, прямая АВ описывает поверхность (развертывающийся геликоид), которая и является боковой поверхностью зуба.

В любом торцовом сечении этой поверхности получаем эвольвенту, а в сечении соосной цилиндрической поверхностью - винтовую линию.

Преимущества косозубой передачи в сравнении с прямозубой:

1. Большая нагрузочная способность (за счет большей суммарной длины контактных линий).

2. Меньшие габариты.

3. Большая плавность и бесшумность работы.

4. Более равномерный износ.

Недостатком косозубой передачи является наличие осевой силы (рис.5.11), которая дополнительно нагружает опоры, увеличивая их размеры, массу и стоимость.

Рис.5.10

Рис.5.11

Рис.5.12

5.3.1 Основные размеры косозубых колес

В отличие от прямозубых, у косозубых колес различают два модуля - окружной и нормальный.

Окружной модуль m_t (как и для прямозубых колес) - это расстояние между одноименными профилями двух соседних зубьев, измеренное по дуге окружности.

Нормальный модуль m - это кратчайшее расстояние по какой-либо соосной цилиндрической поверхности между эквидистантными (равноотстоящими) одноименными линиями соседних зубьев (рис.5.12).

Модули связаны между собой соотношением:

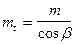, (5.35)

где b - угол наклона линии зуба на делительном цилиндре.

Для возможности нарезания косозубых колес стандартным режущим инструментом стандартизирован нормальный модуль.

Диаметр делительной окружности рассчитывается как

d = m_tZ = . (5.36)

Межосевое расстояние передачи без смещения

a = r₁ + r₂ = 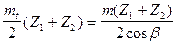. (5.37)

Высота головки зуба

h_a = h_a*m

Высота ножки зуба

h_f = (h_a* +C*)m,

где, как и для прямозубых колес с нормальной высотой зуба, стандартные значения коэффициентов составляют

h_a* = 1, С* = 0,25.

Диаметр окружности впадин

d_f = d - 2h_f.

Диаметр окружности вершин

d_a = d +2h_a.

При выборе угла наклона линии зуба можно руководствоваться следующими рекомендациями:

1. При нежелательности возникновения больших осевых усилий b = 7°...10°.

2. В особо быстроходных передачах для уменьшения шума угол b увеличивается до 30°...35°.

3. В тяжело нагруженных передачах угол b выбирают из условия

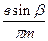= целое число (1;2;3...),

где в - ширина зубчатого венца. В этом случае суммарная длина контактных линий максимальна и постоянна.

4. В шевронных передачах угол b может быть увеличен до 40-45°.

Более подробный расчет цилиндрических и иных зубчатых колес изложен, например, в [1, 2, 3].

5.4 Многозвенные зубчатые передачи с неподвижными осями вращения колёс

Простейшая или одноступенчатая зубчатая передача состоит из двух колёс, находящихся в зацеплении друг с другом. Зацепление может быть внешним или внутренним, в связи с чем передачи делятся на передачи внешнего и внутреннего зацепления. На рис.5.13 показаны схемы изображения одноступенчатой передачи внешнего (см. рис. 5.13.а) и внутреннего (см. рис. 5.13. б) зацепления.

Буквами О₁ и О₂ обозначены геометрические оси вращения колёс, r₁ и r₂ - радиусы их делительных окружностей, которые в данном случае совпадают с начальными : w₁ и w₂ - угловые скорости, P₁₂ – полюс зацепления. Если геометрические оси вращения колес передачи неподвижны в пространстве, то такую передачу называют передачей с неподвижными осями. Ведущим называется колесо, к которому приложен движущий момент. Ведомым - колесо, которое получает вращение от ведущего ; к ведомому колесу приложен момент сопротивления. Передаточным отношением называется отношение угловых скоростей колес. Его обозначают U с двумя цифровыми индексами, которые указывают отношение угловых скоростей каких колёс это передаточное отношение выражает. Так, U₁₂ - это передаточное отношение от первого колеса ко второму. U₁₂ = w₁ /w₂.

В общем случае : U_{вщ. вм.}. = w_вщ/ w _вм , (5.38)

где - вщ –ведущее колесо, вм - ведомое колесо.

Поскольку линейные скорости колес в полюсе зацепления одинаковы, т.е.

V₁ = w₁ r₁ ; V₂ = w₂ r₂,

V₁ = V₂ = w₁ r₁= w₂ r₂, (5.39)

то можно получить выражение передаточного отношения одноступенчатой передачи через радиусы или числа зубьев колёс:

U₁₂ = w₁ /w₂ = ±r_w2/ r _w1 = ±r₂/ r₁ = ±Z₂/Z₁, (5.40)

Рис.5.15

Рис.5.14

Рис.5.13

где r_w1, r_w2, r₁ ,r₂ ,Z₁ ,Z₂ – соответственно радиусы начальных и делительных окружностей и числа зубьёв первого и второго колёс.

При выражении передаточного отношения через радиусы или числа зубьев колёс, для учёта направления вращения колёс, передаточному отношению присваивается знак минус (колёса вращаются в разные стороны), если это передача внешнего зацепления, и знак плюс для передачи внутреннего зацепления (колёса вращаются в одном направлении). Для рис. 5.13,а:

U₁₂ = w₁ /w₂ = - r₂/ r₁ = - Z₂/Z₁. (5.41)

Для рис. 5.13,б:

U₁₂ = w₁ /w₂ = r₂/ r₁ = Z₂/Z₁. (5.42)

Одноступенчатые передачи, как правило, применяются при передаточных отношениях до пяти-шести. Для получения больших передаточных отношений и для уменьшения габаритов применяются многоступенчатые передачи, составленные из нескольких последовательно соединённых между собой одноступенчатых зубчатых передач, как это представлено, например, на рис.5.14.

При этом колёса 1 и 2 образуют первую ступень, колёса 3 и 4 – вторую ступень, колёса 5 и 6 – третью ступень.

Определим передаточное отношение каждой ступени в отдельности:

U_I = U₁₂ = w₁ /w₂ = - r₂/ r₁,

U_II = U₃₄ = w₃ /w₄ = - r₄/ r₃,

U_III = U₅₆ = w₅ /w₆ = r₆/ r₅, где

U_I, U_II, U_III - передаточное отношение соответственно первой, второй, третьей ступени.

Перемножим полученные передаточные отношения с учётом того, что w₂ = w₃,

w₄ = w₅:

U_I U_II U_III = U₁₂ U₃₄ U₅₆ = 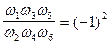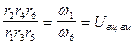. (5.43)

 

В общем случае

U_{вщ. вм.}. = w_вщ/ w _вм = (-1)^к 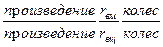, (5.44)

 

где к – число внешних зацеплений.

 

Для зубчатой передачи, изображенной на рис.5.15, передаточное отношение определится как:

U₁₃= w₁ /w₃ =(-1)² 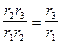(5.45)

Колесо 2 является одновременно ведущим (в паре колес 2-3) и ведомым (в паре 1-2) и называется паразитным. Паразитное колесо не влияет на величину передаточного отношения, а влияет только на его знак.

 

5.5 Зубчатые передачи с подвижными осями вращения колёс (планетарные зубчатые механизмы)

5.5.1 Структура планетарных зубчатых механизмов

 

Как уже отмечалось, планетарными зубчатыми механизмами называют механизмы, в которых имеются зубчатые колёса, перемещающиеся в пространстве.

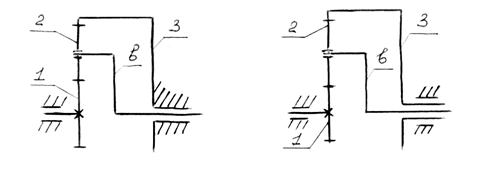
Колёсо 2 (рис.5.16) с движущимися осями вращения колёс носят название сателлитов. Колёса 1 и 3 - центральными. Звено “в”, которое перемещает оси сателлитов, называется водилом. Центральные колёса и водило в планетарном механизме соосны, т.е. их геометрические оси совпадают.

Планетарные механизмы подразделяются на простые планетарные, дифференциалы и сложные планетарные.

К простым планетарным относятся четырёхзвенные механизмы, у которых одно из центральных колёсо закреплено (рис. 5.16,а), т.е. является неподвижным. Это неподвижное центральное колесо носит название опорного. Простой планетарный механизм имеет одну степень свободы, передаточное отношение в этом механизме имеет вполне определённое значение.

К дифференциалам относятся механизмы (рис. 5.17, б) у которых нет опорного колеса, оба центральных колеса в них вращаются. Дифференциал имеет две степени свободы, т.е. при заданном повороте одного его центрального звена повороты двух других не являются определёнными.

 

5.5.2 Определение передаточного отношения планетарных механизмов

Так как в планетарных и дифференциальных механизмах имеются колёса, которые совершают сложное движение – сателлиты, а также водило, не являющееся зубчатым колесом, то расчёт передаточного отношения этих механизмов требует специальных методов.

 

Рис.5.16 Рис.5.17

 

 

а) Аналитический метод (метод Виллиса).

Аналитический метод основан на преобразовании простого планетарного механизма в зубчатую передачу с неподвижными осями вращения колёс с последующим определением передаточного отношения по формуле (5.44).

Метод Виллиса состоит в следующем: мысленно всем звеньям механизма сообщается дополнительное движение, обратное движению водила. В результате сложения действительного и дополнительного движений водило останавливается и механизм преобразуется в зубчатую передачу с неподвижными осями вращения колес, после чего определяется передаточное отношение между центральными звеньями, которое выражается через радиусы или числа зубьев колёс. Полученный механизм называется приведенным или обращенным.

Если заданный механизм является простым планетарным, то полученное уравнение оказывается достаточным для непосредственного определения из него передаточного отношения заданного механизма.

Если механизм является сложным планетарным, его мысленно разделяют на составляющие механизмы.

Далее, применяя метод обращения движения (метод Виллиса) к тем механизмам, которые являются планетарными, определяют передаточные отношения между центральными звеньями приведенных механизмов, связывая тем самым их угловые скорости ( в обращенном движении). Решая затем полученную систему из двух уравнений, находят искомое передаточное отношение исходного механизма.

Если один из составляющих механизмов не является планетарным, то к нему метод Виллиса не применяется, (передаточное отношение определяется сразу через числа зубьев или радиусы колес).

Пример.

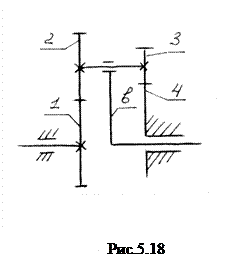
На рис.5.18 изображен простой планетарный механизм, состоящий из центрального колеса 1, сателлитов 2 и 3, опорного колеса 4 и водила “в”. Требуется определить передаточное отношение U_IB от колеса 1 к водилу “в”, считая радиусы колёс известными.

В действительном движении звенья механизма имеют угловые скорости w_1, w₂, w₃, w_в, w₄=0. Сообщим мысленно всему механизму дополнительное движение, обратное движению водила (-w_B). В результате сложения действительного и дополнительного движений водило останавливается, а другие звенья будут двигаться с угловыми скоростями:

w₁^в= w₁ - w_в, (5.46)

w₄^в= - w_в, (5.47)

w_в=0,

w^В₂= w₃^в = w₂ - w_в = w₃- w_в.

Знак “в” в обозначениях угловых скоростей показывает, что соответствующие скорости являются скоростями звеньев в приведённом механизме, у которого остановлено водило. Удобно вышеописанные преобразования угловых скоростей свести в таблицу:

 

Звенья Тип движения	Центральные звенья
			В
Действительное Дополнительное Суммарное	w1 - wв w1 - wв	w4=0 -wв -wв	wв -wв

 

Далее составляем уравнение передаточного отношения между центральными звеньями в приведённом механизме и выражаем его через радиусы или числа зубьев колёс.

U^в₁₄ = w^в₁/ w₄^в = (w₁-w_в)/-w_в = - w₁/ w_в +1=1-U⁴_1в, откуда (5.48)

U^в₁₄ =1- U⁴_В, (5.49)

U⁴_1в =1- U^в₁₄ , (5.50)

т.е. передаточное отношение от колеса к водилу равно единице минус передаточное отношение от того же колеса к другому центральному, но в приведённом механизме, полученном из этого же планетарного механизма методом остановки водила.

U^в₁₄= U^в₁₂ U^в₃₄ = (-Z₂/Z₁) (-Z₄/Z₃), (5.51)

U⁴_1в =1 - (Z₂ Z₄/ Z₁ Z₃). (5.52)

Применение формулы Виллиса для схем простых планетарных механизмов.

Для механизма на рис. 5.16:

U³_1в=1-U^в₁₃, (5.53)

U^в₁₃=Uв₁₂U^в₂₃=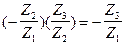, (5.54)

U³_1в=1+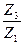; U³_в1=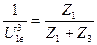. (5.55)

Для механизма на рис.5.19:

U⁴_1в=1-U^в₁₄, (5.56)

U^в₁₄=U^в₁₂U^в₃₄=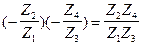, (5.57)

U^в₁₄=1-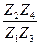. (5.58)

б) Графический метод.

Основан на использовании плана скоростей механизма.

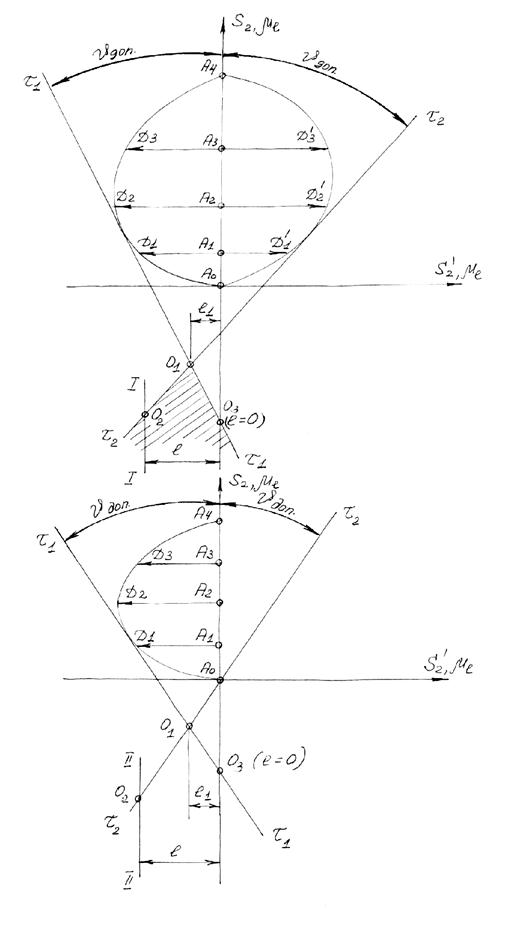
Если в точке О находится центр вращения звена, то геометрическое место концов векторов скоростей точек звена, расположенных на оси ОУ, представляет собой прямую, соединяющую конец вектора скорости точки А и начало координат. Эту прямую называют линией распределения скоростей точек звена (рис. 5.20).

Выразим угловую скорость звена 1 через скорость точки А:

w₁ = V_A / r_OA = 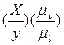= tg d (m_v /m_l), (5.59)

здесь m_v [м /с мм] и m_l[м/мм] - соответственно масштабные коэффициенты по осям абсцисс (скоростей) и ординат (радиусов).

Эта формула показывает, что угловая скорость звена пропорциональна тангенсу угла наклона линии распределения скоростей точек звена к оси радиусов.

Для двух звеньев А и В передаточное отношение с учётом последней формулы будет иметь вид:

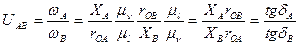. (5.60)

Если принять r_OA= r_OB, то получим:

U_АВ = w_A/w_B = tg d_A/tgd_B =X_A/X_B. (5.61)

При этом, если углы (как и соответствующие им отрезки) расположены в одной четверти, то передаточному отношению присваивается знак «+», если в разных - знак «-».

Последовательность определения передаточного отношения графическим методом следующая:

1. Размещаем начало прямоугольной системы координат V и r на центральной оси механизма.

2. Задаёмся окружной скоростью в полюсе зацепления одной из пар колес, изображая эту скорость в выбранной системе координат отрезком произвольной длины, параллельным оси V в произвольном направлении, на соответствующем расстоянии.

3. Соединяем конец этого отрезка с точкой О – центром системы координат, где все центральные звенья имеют скорость, равную нулю, т.е. проводим линию распределения скоростей точек звена.

4. Используя точки, в которых скорости сопряжённых звеньев равны между собой –

 

 

Рис.5.20

Рис.5.19

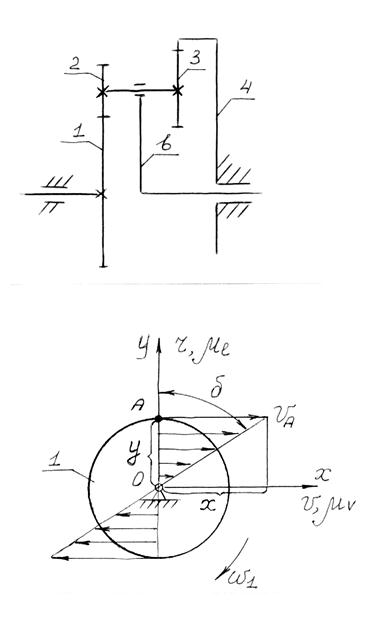
-полюсы зацепления Р, последовательно строим линии распределения скоростей для всех остальных звеньев механизма. В результате получаем картину скоростей механизма.

5. По картине скоростей определяем передаточное отношение, для чего в произвольном месте пересекаем горизонталью линии распределения скоростей тех колёс, передаточное отношение между которыми ищем. Измеряем длины отрезков по горизонтали, заключенные между осью радиусов и линиями распределения скоростей звеньев и рассчитываем передаточное отношение, как отношение измеренных отрезков.

Пример.

Для простого планетарного механизма, изображённого на рисунке 5.21.а, определить передаточное отношение U_1в графическим способом.

Задаёмся окружностью точки конца водила “в”, которая совпадает с подвижной геометрической осью блока сателлитов 2-3. Эту скорость изображаем вектором произвольной длины V_в, расположенным параллельно оси V на уровне выбранной точки. (рис. 5.20). Чтобы построить линию распределения скоростей звена, необходимо знать скорости двух его точек. На водиле скоростью одной точки мы задались, а скорость точки, лежащей на центральной оси механизма, равна нулю. Соединив конец вектора скорости водила V_в с началом координат –точкой О, получим линию распределения скоростей водила “в”.

Скорость одной точки блока сателлитов 2-3-оси известна, а второй известной точкой будет полюс Р₃₄ зацепления колеса 3 и опорного колеса 4. Поскольку скорость любой точки колеса 4 равна нулю, ввиду того, что оно неподвижно, то и скорость сателлита 3 в полюсе Р₃₄ равна нулю. Соединив прямой линией конец вектора V_В,2,3 с точкой О^¢, получим линию распределения скоростей блока сателлитов 2-3. На вертикальной оси отмечаем цифрами 3 и 4 и точку О^¢, в которой скорость полюса Р₃₄ равна нулю.

В полюсе зацепления Р₁₂ окружные скорости колёс 1 и 2 равны между собой. Скорость колеса 2 определяется с помощью построенной линией распределения скоростей блока сателлитов 2-3. Для этого на уровне точки Р₁₂ проводим горизонталь до пересечения с линией распределения скоростей саттеллита. Полученный отрезок V₁₂, заключённый между

 

 

б)

а)

Рис.5.21

Рис.5.22

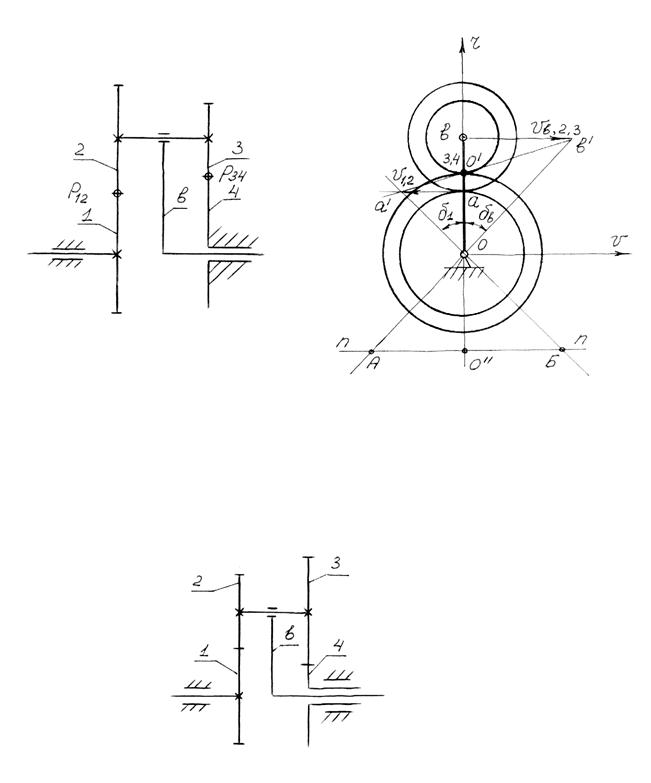
вертикальной осью и линией распределения скоростей 2-3, представляет собой скорость полюса зацепления Р₁₂. Поскольку скорость точки колеса 1, лежащей на центральной оси, равна нулю, то, соединив полученный отрезок с началом координат, получаем линию распределения скоростей колеса 1.

В соответствии с вышеизложенным

U_1В = w₁/w₂ = - tg d₁/tgd_B = - О^²Б/O^²A. (5.62)

 

Выразим искомое передаточное отношение через радиусы колёс:

U_1В = w₁/w₂= - tg d₁/tgd₂ = -(аа^¢/оа)/(вв^¢/ов) = -(аа^¢(r₁ +r₂))/(вв^¢/(r₁)). (5.63)

Из подобия треугольников аа¢/вв^¢ = о^¢а/о^¢в = (r₂ – r₃)/r₃. Тогда

U_1B=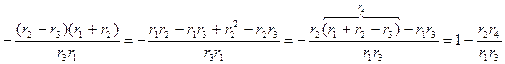, (5.64)

где r₁+r₂-r₃=r₄.

Аналитический метод (метод Виллиса) приводит к такому же результату (см.5.52):

U_1В⁴ = 1 - U₁₄^В = 1 – (r₂r₄)/ (r₁r₃).

 

5.5.3 Планетарные механизмы с дифференциальной связью между звеньями

Применим метод Виллиса к дифференциалу. (рис.5.22)

U_1В⁴ = , (5.65)

w₁ – w_В = w₄ U^В₁₄– w_В U^В₁₄ , (5.66)

w₁ = w₄ U^В₁₄– w_В U^В₁₄ + w_В , (5.67)

w₁ = w₄ U^В₁₄ + w_В(1- U^В₁₄), где (5.68)

U⁴_1В =1- U^В₁₄, тогда (5.69)

w₁ = w₄ U^В₁₄ + w_В U^В₁₄, (5.70)

аналогично:

w₄ = w₁ U^В₄₁ + w_В U¹_4В, (5.71)

w_В= w₁ U⁴_В1 + w₄ U¹_В4. (5.72)

В дифференциале подвижны три соосных звена: два центральных колеса и водило. Угловая скорость любого из соосных звеньев дифференциала равна сумме угловых скоростей двух остальных звеньев, причём каждая из этих угловых скоростей найдена при условии остановки другого соосного звена

 

5.5.3.1 Дифференциал автомобиля

Привод ведущих колес большинства автомобилей осуществляется через дифференциал с коническими колёсами (рис.5.23). При повороте ведущих колёс автомобиля (рис.5.24) колесо 1, катящееся по внешней кривой должно пройти больший путь, чем колесо 2, катящееся по внутренней кривой. Дифференциал позволяет левым и правым колесам двигаться с различными угловыми скоростями. Вращение передаётся от двигателя через коническую передачу (рис.5.23), одно из колёс которой является водилом “в” дифференциала. Сателлит 3 находится в зацеплении с одинаковыми центральными колёсами 1 и 2, закреплёнными на полуосях А и В.

Формула, связывающая угловые скорости центральных колёс и водила, имеет вид:

, отсюда (5.73)

w₁ –w_B = - w₂ +w_B или (5.74)

w₁+ w₂ = 2 w_B (5.75)

В формуле (5.75) известной является только w_B. Определенность в движении колес зависит от условий движения автомобиля. Здесь возможны три варианта:

1) Если автомобиль двигается по прямой, то V₁ = V₂, w₁ = w₂ – дифференциал не работает и равенство (5.75) имеет вполне определённое значение: w₁ = w₂ = w_В.

2) Если колесо, например 1, остановится то w₁ =0, тогда получим:

w_B = w₂/2, т.е. колесо 2 будет делать в 2 раза больше оборотов, чем водило.

3) если автомобиль делает поворот (рис.5.24), то угловые скорости связаны соотношением:

w₁/w₂ = V₁/V₂ = (А+а)/(А-а).

 

5.5.4 Определение передаточного отношения замкнутых дифференциалов

Дифференциал имеет две степени свободы, т.е. при заданном повороте одного его центрального звена повороты двух других не являются определёнными. Для устранения указанной неопределённости какие-либо два из трёх соосных звеньев дифференциала соединяют между собой дополнительной передачей, которая носит название замыкающей цепи. Замыкающая цепь может быть выполнена в виде зубчатой передачи с неподвижными осями вращения колёс или в виде простого планетарного механизма. Дифференциал, у которого имеется замыкающая цепь, носит название замкнутого.

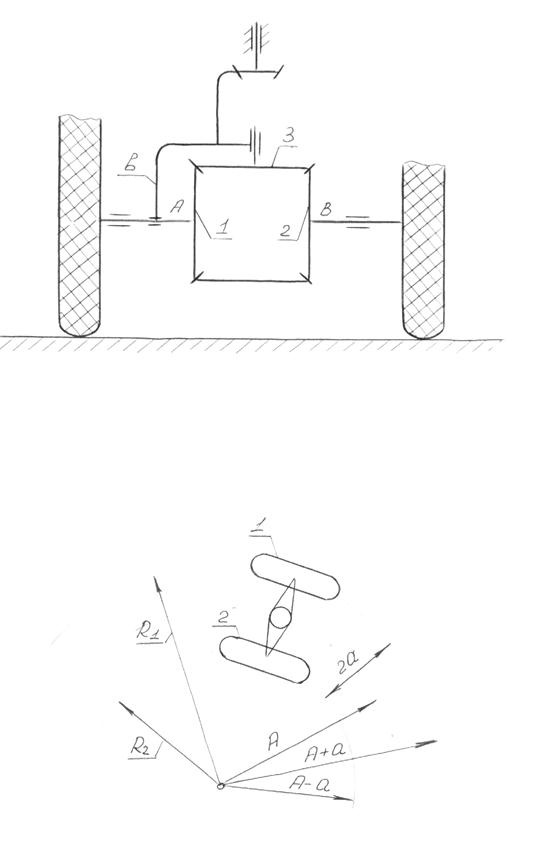
Рассмотрим, например, дифференциал с замыкающей цепью, изображенный на рис. 5.25.

	Рис. 5.23
		Рис. 5.24

 

 

Звенья 1, 2, 3, 4, ²в²– образуют дифференциал , звенья 5, 6, 7, 8 – замыкающую цепь. Определим передаточное отношение от входного вала к выходному, т.е. U_1В.

Применив метод Виллиса к собственно дифференциалу, составим уравнения, связывающие угловые скорости соосных звеньев приведенного механизма:

U₁₄^В = (w₁ – w_В)/ (w ₄ – w_В) = 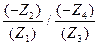= (Z₂ Z₄)/( Z₁ Z₃). (5.76)

 

Для замыкающей цепи имеем:

U₅₈ = w₅/w₈ = 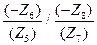= Z₆ Z₈ / Z₅ Z₇ = w₄/w_B, так как (5.77)

w₄=w₅ и w_в=w₈.

После совместного решения этих уравнений получаем:

U_1в = 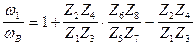. (5.78)

Для графического решения данного дифференциала с замыкающей цепью надо, как было указано выше, найти линии распределения скоростей входного и выходного звеньев, построив для этого план скоростей механизма (рис.5.25).

 

5.5.5 Синтез планетарных механизмов

При проектировании планетарных зубчатых передач можно выделить следующие этапы:

1) Выбрать схему планетарного механизма, обеспечивающую заданное передаточное отношение.

В качестве примера выберем простой планетарный механизм с двойным сателлитом, одним внешним и одним внутренним зацеплением (рис.5.26).

Уравнение, связывающее передаточное отношение U_1В с числом зубьев колёс механизма имеет вид:

U_1В⁴ = 1 - U₁₄^В = 1 + Z₂ Z₄/ Z₁ Z₃.

2) При подборе чисел зубьев колёс передачи необходимо обеспечить правильное зацепление, т.е. условие отсутствия заклинивания, а именно: исключить подрезание профиля зуба, не допустить заострения зубьев на окружности вершин и не допустить интерференцию зубьев. Таким образом задача определения числа зубьев сводится к составлению исходных уравнений, отражающих указанные условия для каждой конкретной пары, и совместному их решению.

Рис.5.25

Рис.5.26

3) Необходимо выполнить условия, специфические для планетарных механизмов: обеспечить условия соосности, соседства и сборки. Рассмотрим эти условия.

А) условие соосности требует, чтобы валы центральных звеньев были соосными, так как сателлит или блок сателлитов зацепляются одновременно с обоими центральными колесами:

r_w1 + r_w2 = r_w4 - r_w3 . (5.79)

Для колеса без смещения r_wi = r_i. Тогда, с учетом того, что r_i = mZ_i/2, будем иметь:

r₁ +r₂ = r₄ –r₃ или: (5.80)

Z₁ + Z₂ = Z₄ – Z₃ . (5.81)

Б) Условие соседства требует, чтобы соседние сателлиты не задевали друг друга своими зубьями. Необходимо назначать числа зубьев колёс так, чтобы расстояние между осями соседних сателлитов было больше диаметра окружности вершин наибольшего из сателлитов:

О₁О_2¢>2 r_a3. (5.82)

Если сателлиты расположены под углом 2p/к (рад), где к – число блоков сателлитов, то sin p/к = О₂А/ О₁О₂:

О₂А = О₁О₂ sin p/к = (r₁ +r₂) sin p/к, (5.83)

О₁О_2¢ = 2 О₂А = 2(r₁ +r₂) sin p/к, (5.84)

2 (r₁ +r₂) sin p/к >2 r_a3. (5.85)

В частном случае для передачи без смещения:

(m Z₁ +m Z₂) sin p/к > m Z₃ + h_a3, где (5.86)

2 2 2

h_{a 3} = h_a* m, h_a* = 1, или:

sin p/к> (Z₃ + 2h^*a)/( Z₁ + Z₂). (5.87)

В) Условие сборки.

Это условие, обеспечивающее одновременное зацепление всех сателлитов с центральными колёсами. При сборке планетарного механизма вводим следующие допущения:

- равномерное распределение сателлитов по общей окружности (равные углы между осями сателлитов);

-одинаковая ориентация зубьев друг относительно друга в каждом блоке сателлитов (рис.5.26);

- каждый блок сателлитов устанавливается на свою ось в водиле в одном и том же положении, когда центр сателлита располагается на вертикали, проходящий через ось центральных колёс и ось симметрии впадины зуба этих колёс.

После установки первого блока сателлитов первое подвижное центральное колесо принимает строго определённое положение. Если не выполнить ряд требований, то при установке следующих блоков сателлитов их зубья могут не оказаться точно против впадины одного из центральных колес и тогда осуществить сборку механизма невозможно. Необходимо так подобрать число зубьев Z, чтобы зубья всех сателлитов точно вошли во впадины центральных колёс.

Поставив первый сателлит на ось, когда она занимает “вертикальное” положение, поворачиваем водило на угол j_В = 2 pк + 2 pn, где n –число полных оборотов водила. При этом первое колесо тоже повернется на некоторый угол j₁ = j_В U_1В.

Ставим второй сателлит на свою ось в вертикальном положении, но он войдёт на своё место в том же вертикальном положении, когда зацепляющееся с ним центральное колесо 1 повернется на целое число угловых шагов (целое число зубьев), т.е.

j₁ =С t = С2p/Z₁, где С –любое целое число, а t =2p/Z₁. (5.88)

Делая подстановку, получаем:

С 2p/Z₁ = j_В U_1В, (5.89)

С 2p/Z₁ = (2p/к + 2pn) U_1В, откуда С=(1+кn) Z₁ U_1В/к. (5.90)

Здесь возможно два варианта:

1) Если Z₁U_1В/к – целое число, то для установки следующего сателлита достаточно повернуть водило на угол j_В= 2p/ к.

2) Если Z₁ U_1В/к – не целое число, то надо подобрать ²n² таким образом, чтобы «С» стало целым.

В случае, когда при любом ²n² величина ²С² не является целым числом, должна выполняться индивидуальная сборка механизма.

6 Синтез кулачковых механизмов

 

Кулачковым называется механизм, в состав которого входит кулачок. Кулачок - звено, имеющее элемент высшей пары, выполненный в виде поверхности переменной кривизны. Простейший кулачковый механизм состоит из кулачка, толкателя и стойки. Кулачковыми механизмами можно обеспечить практически любой закон движения выходного звена.

 

6.1 Виды кулачковых механизмов

Различают плоские и пространственные кулачковые механизмы. К плоским относятся кулачковые механизмы с дисковыми кулачками (рис.6.1) и механизмы с поступательно движущимся плоским кулачком (рис.6.2).

К пространственным относятся механизмы с цилиндрическим, коническим и более сложной формы кулачками.

Кулачковые механизмы различают по:

1) характеру движения кулачка:

а) с вращающимся кулачком (рис.6.1),

б) с поступательно движущимся кулачком (рис.6.2),

в) с неподвижным кулачком.

2) по характеру движения толкателя:

а) с поступательно движущимся толкателем (рис.6.2),

б) с вращающимся толкателем (рис.6.1),

в) с толкателем, совершающим сложное движение (рис.6.3)

3) по характеру рабочей поверхности толкателя:

а) с заострённым толкателем (рис.6.4,а),

б) с роликовым толкателем (рис.6.4,б),

в) с плоским тарельчатым толкателем (рис.6.4,в),

г) с криволинейным толкателем (рис.6.4,г).

Рабочая поверхность толкателей, воспринимающая нагрузку от кулачка, подвержена износу. Чтобы уменьшить износ, применяют толкатели различной конструкции. Применение роликов позволяет исключить трение скольжения, заменив его трением качения, тем самым уменьшить износ элементов высшей пары и повысить надёжность механизма.

4) по характеру замыкания высшей пары:

а) с геометрическим замыканием (рис.6.5.),

б) с силовым замыканием (рис.6.6).

При работе кулачкового механизма необходимо обеспечить постоянное соприкасание входного и выходного звеньев. Это соприкасание может быть обеспечено, например, чисто

Рис.6.1

Рис.6.5

Рис.6.6

г)

в)

б)

а)

Рис.6.4

Рис.6.3

Рис.6.2

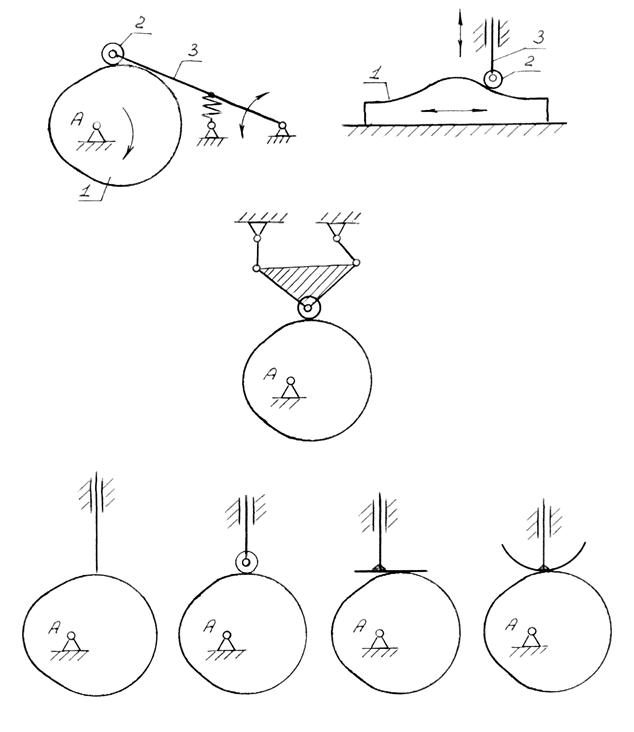
геометрически, если выполнить профиль кулачка в форме паза, боковые поверхности которого огибают ролик. Пазовые кулачки обеспечивают геометрическое (кинематическое) замыкание высшей пары. При геометрическом замыкании кулачок является ведущим звеном как при подъёме, так и при опускании (рис.6.5).

При силовом замыкании кулачок является ведущим звеном при подъёме толкателя, а опускание происходит за счёт силы тяжести толкателя или за счет упругости пружины (рис.6.6).

 

6.2 Этапы синтеза кулачковых механизмов

При проектировании кулачковых механизмов можно выделить следующие основные этапы:

1) выбор схемы механизма,

2) выбор закона движения выходного звена (т.е. толкателя) в функции угла поворота кулачка,

3) определение основных размеров,

4) аналитический расчёт координат профиля кулачка или графическое построение профиля.

Схема кулачкового механизма выбирается из условий его работы на основании имеющегося опыта.

 

6.2.1 Выбор закона движения выходного звена

Законом движения толкателя называют функцию перемещения (углового или линейного) толкателя по времени или по обобщённой координате, т.е. углу поворота кулачка j_К.

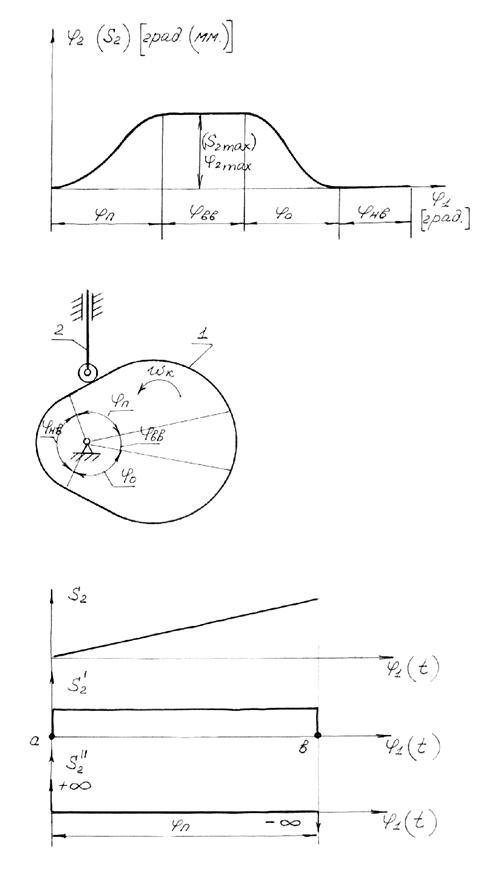
На рисунке 6.7 приведён типовой закон движения толкателя.

При равномерном вращени кулачка движение толкателя имеет 4 фазы:

1) фаза подъёма j_П,

2) фаза верхнего выстоя j_ВВ,

3) фаза опускания j_О ,

4) фаза нижнего выстоя j_НВ.

При этом j_П + j_ВВ+ j_О + j_НВ = 360°. (6.1)

На кулачке фазовые углы j_П , j_ВВ, j_О , j_НВ совпадают с углами профиля только в центральном кулачке (рис.6.8)

 

Рис.6.9

Рис.6.8

Рис.6.7

Закон движения толкателя и соотношения между фазовыми углами выбираются в соответствии с технологическим процессом и из условия согласованной работы отдельных механизмов, входящих в состав машины.

Под законом движения толкателя понимают не только функцию перемещения, но и ее производные, взятые по времени или по обобщенной координате.

Во многих случаях кулачковый механизм должен обеспечить лишь требуемую величину хода выходного звена на заданном угле поворота кулачка, а закон движения толкателя при этом несущественен (с точки зрения технологического процесса).

В этих случаях, особенно в быстроходных машинах, где силы инерции велики (F_ин=ma_2, (где a₂ = d²S₂/dt² = S₂^¢¢w₁; S₂^¢¢ = d²S₂/d²j₁), при выборе закона движения толкателя исходят из такого закона изменения его ускорения а₂ (или аналога ускорения S₂^¢¢), который обеспечивает с одной стороны - плавное изменение ускорения, с другой – по возможности меньшую его величину.

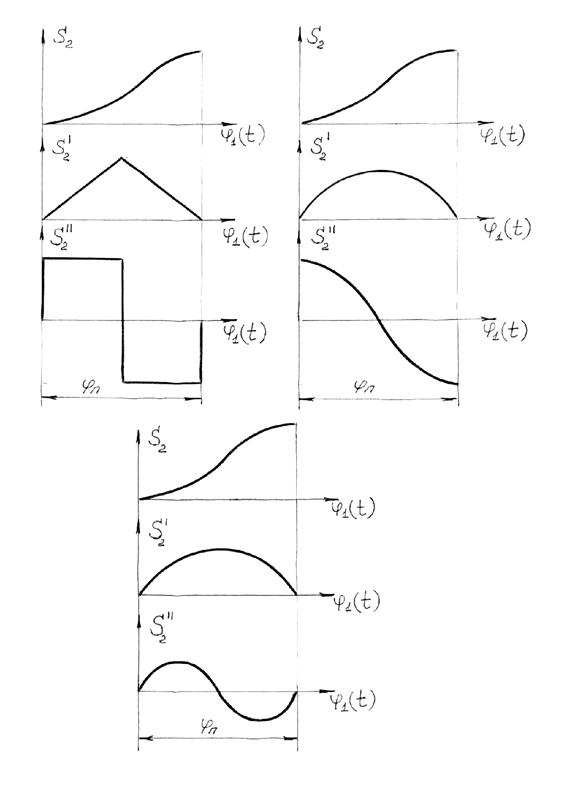
При этом часто используются приведенные на рис.6.9, 6.10 законы движения толкателя.

Минимальная величина ускорения толкателя обеспечивается законом постоянного ускорения (рис.6.10,а), но он, как и закон косинусоидальных ускорений (рис.6.10,б), имеет недостаток, выраженный в мгновенном изменении ускорений на конечную величину - так называемые мягкие удары. Они допускаются, но нежелательны, т.к. приводят к вибрациям.

Наиболее плавно изменяются ускорения по синусоидальному закону (рис.6.10,в), но при этом величина а_2maх больше.

Помимо «мягких» ударов, в механизме могут возникнуть «жесткие» удары, когда ускорение толкателя меняется мгновенно на бесконечно большую величину (рис.6.9). Соответственно, на бесконечно большую величину должны меняться и силы инерции (теоретически, т.к. за счет упругости звеньев силы инерции до бесконечности не увеличиваются), что недопустимо.

Чтобы избежать этого, в местах мгновенного изменения ускорения вводят «сглаживающие» участки.

6.3 Определение основных размеров кулачкового механизма

Основным условием синтеза кулачковых механизмов является обеспечение заданного закона движения выходного звена. В качестве дополнительного условия синтеза во многих механизмах является ограничение по углу давления, от которого зависят величины сил, действующих в механизме и его КПД.

 

в)

б)

а)

Рис.6.10

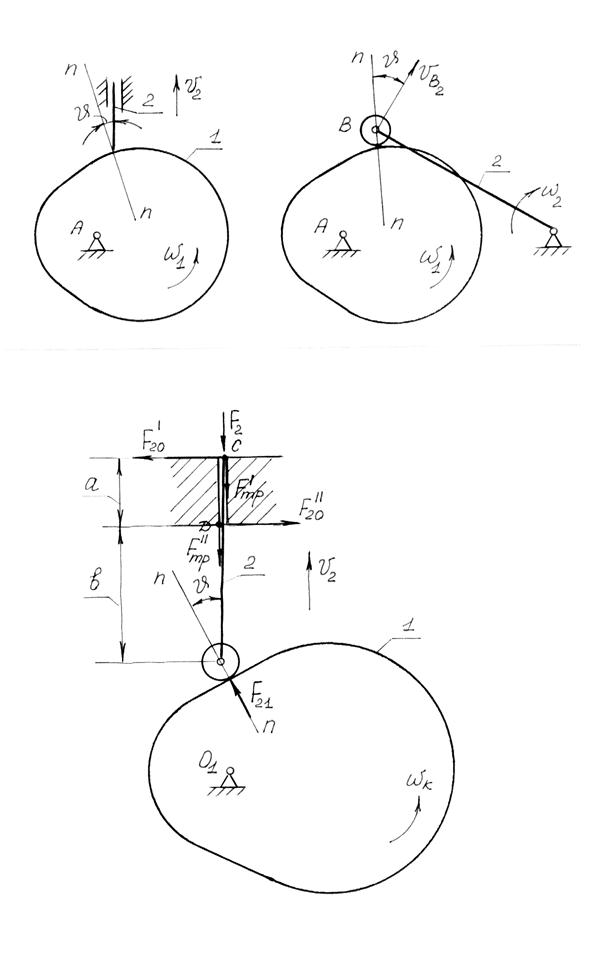
Углом давления в кулачковом механизме называется угол между нормалью к профилю кулачка в точке его касания с толкателем и направлением абсолютной скорости толкателя. (рис.6.11, 6.12).

 

6.3.1 Силы в кулачковом механизме

Определим, с какой силой F₂₁ кулачок должен действовать на толкатель, чтобы преодолеть силу F₂ (силу полезного сопротивления) (рис.6.13).

Допущения:

1) Учитываем перекос толкателя в направляющих вследствие зазора между толкателем и направляющими стойки (точки С и Д).

2) Учитываем трение только в направляющих (в паре толкатель – стойка). Трение между кулачком и толкателем во внимание не принимаем, так как толкатель снабжён роликом.

3) Толщиной штанги толкателя пренебрегаем, считая моменты силы трения и силы F₂

относительно точек приложения нормальных реакций равными нулю.

Из условия равновесия толкателя:

åМс = 0:

F₂₀^¢¢а - F₂₁ (а + в) sinn= 0, (6.2)

F₂₀^¢¢ = F₂₁ (а+в) sinn.

а (6.3)

åМд = 0:

F₂₀^¢а - F₂₁в sinn= 0, (6.4)

F₂₀^¢= (F₂₁/а в) sinn, (6.5)

где ²а² – длина направляющей, ²в² – вылет толкателя.

åFу = 0:

F₂₁cos n- F₂ – F_тр^¢ - F_тр^¢¢ = 0, где (6.6)

F_тр^¢ = f F₂₀^¢, (6.7)

F_тр^¢¢ = f F₂₀^¢¢. (6.8)

После подстановки получим:

F₂₁cos n- F ₂– f F₂₁ (в sin n)/a- f F₂₁ ((а+в) sinn)/a = 0, (6.9)

F₂₁ = 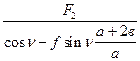. (6.10)

Рис.6.13

Рис.6.11 Рис.6.12

6.3.2 Мгновенный КПД кулачкового механизма

Ранее (см. раздел…3.6.2.) было получено, что для механизма с вращающимися ведущим звеном

h _мгн = - Рвых./Рвход = М^о_дв/М _дв. (6.11)

Для рассматриваемого механизма М^о_дв. = F^о_дв h и М _дв = F _дв h, то h_мгн = F^о_дв/ F _дв, где,

F^о_дв = F^о₂₁ – сила, которая должна быть приложена в идеальном механизме без трения для преодоления силы F₂ (т.е. когда f = 0).

F_дв = F₂₁ – та же сила, но в реальном механизме с трением.

Тогда h_мгн = . (6.12)

Выводы:

1) С увеличением угла давления h_мнг снижается. Поэтому выгодно иметь малые углы давления. Но для получения таких углов давления необходимо увеличивать минимальный радиус r_min кулачка. Поэтому в тех случаях, когда габариты механизма не ограничены, следует брать по возможности больший минимальный радиус кулачка.

2) При больших углах давления в механизме возникает самоторможение.Условие самоторможения: h_мгн. £ 0

Установим, при каком угле давления возникает самоторможение:

1 – f tgn (а + 2в)/a £ 0 (6.13)

tgn_крит = 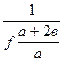, (6.14)

где n_крит. - критическое значение угла давления, при котором возникает самоторможение.

В тех случаях, когда габариты механизма ограничены, угол давления кулачка выбирают по одному из указанных ниже условиях:

а) по величине коэффициента возрастания усилий, который представляет собой отношение силы F₂₁ , которая должна быть приложена к толкателю при данном угле давления, к силе, соответствующей углу давления, равному нулю.

При n =0 F₂₁ = F₂.

Тогда К_n = F₂₁/ F₂ = 1/ (cosn- f sin n (а+2в)/a). (6.15)

Рекомендуется при выборе брать К_n £ 2.

б) по широко распространённой рекомендации: принимать при проектировании допустимый угол давления, величина которого при поступательно движущемся толкателе на фазе подъёма кулачка равна

n_max = 30¸35°, (6.16)

при качающемся толкателе на фазе подъёма

n_max = 45¸50° (6.17)

При силовом замыкании на фазе опускания самоторможение в механизме возникнуть не может, так как движение толкателя на этой фазе происходит под действием силы упругости пружины или силы тяжести толкателя. Поэтому на этой фазе допускаются большие углы давления.

6.3.3 Определение углов давления для кулачкового механизма с поступательно движущимся роликовым толкателем

При поступательно движущемся роликовым толкателе радиус его кривизны равен бесконечности (рис.6.14). Поэтому точка Р-полюс, определяется как точка пересечения общей нормали n-n к профилю кулачка и толкателя в точке их касания и перпендикуляра к линии перемещения толкателя.

В полюсе скорости звеньев равны между собой:

Vp₁ = Vp₂; где Vp₁ =w₁ O₁P; V p₂ = V₂.

Тогда

O₁P = V₂ /w₁ = dS₂/dt₁ = dS₂ = S₂^¢ - аналог скорости толкателя. (6.18)

dj₁/dt₁ dj₁

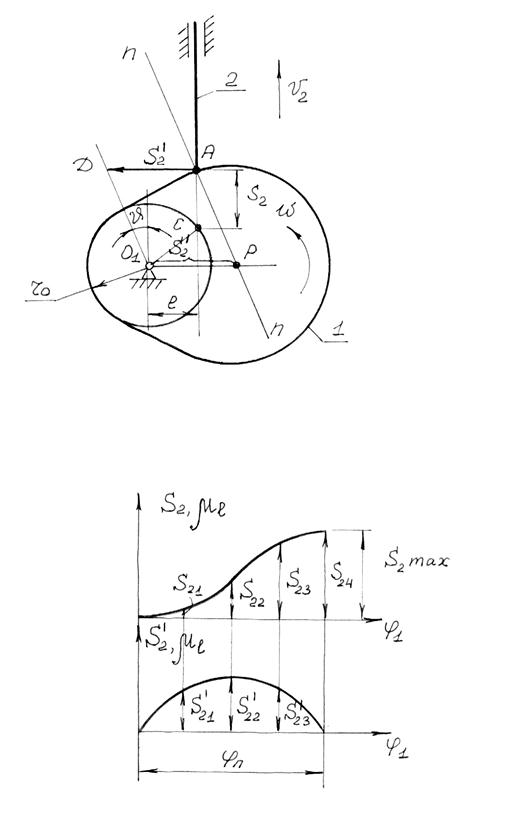
Если из точки А отложить повёрнутый на 90^° по вращению кулачка аналога скорости толкателя и конец этого отрезка (точка Д) соединить с центром вращения кулачка, то линия О₁Д составит с линией толкателя угол, равный углу давления в данном положении механизма. Подобные построения можно выполнить для любого положения механизма и следовательно определить угол давления в любом положении. Для этого удобно построить диаграмму S₂^¢ = S₂^¢ (S₂) (рис.6.15).

Первоначально строится диаграмма S₂= S₂(j₁), а затем S₂^¢ = S₂^¢ (j₁), причём обе диаграммы строятся в одинаковом масштабе m_l. Размечая далее траекторию движения центра ролика по имеющемуся закону его перемещения, в каждом положении откладываем повернутый на 90^° в сторону вращения кулачка аналог A_iD_i скорости толкателя. Соединив плавной линией концы отложенных отрезков, получаем диаграмму аналогов скорости толкателя S^¢ = S₂^¢(S₂) (рис.6.16).

Для нахождения экстремальных значений угла давления достаточно провести из точки О₁ касательные к полученному графику S¢₂ = S¢₂(S₂). Экстремальными значениями угла

 

Рис.6.15

Рис.6.14

 

 

Рис.6.17

Рис.6.16

давления при поступательно движущемся толкателе является угол между касательной к диаграмме и линией перемещения толкателя.

Используя полученную зависимость, можно решить обратную задачу, когда, исходя из заданного допустимого значения угла давления, нужно определить начальный радиус кулачка.

6.3.4 Определение основных размеров дискового кулачка с поступательно движущимся роликовым толкателем

Дано: S´₂ = S´₂(S₂), S_2max, e, r_p, j_п, j_вв, j_о, j_нв, n_доп.

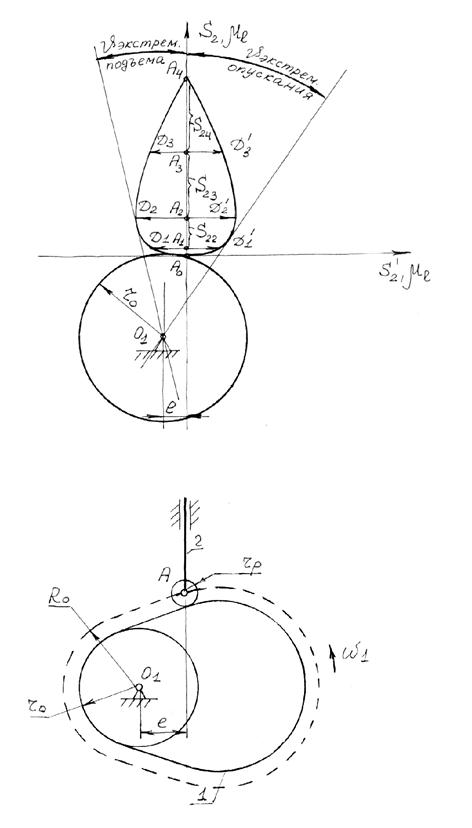
Требуется определить область, в которой можно выбрать центр вращения кулачка, при условии, что угол давления n на фазе подъема не превысит заданный допустимый угол давления, т.е. определить R_0min (рис.6.17).

При определении основных размеров кулачкового механизма с дисковым кулачком к поступательно движущимся роликовым толкателем при силовом замыкании исходим из условия, что угол давления ни в одном из положений не должен превышать 30° (n_доп. = 30°).

При решении задачи используем диаграмму аналога скорости толкателя Sґ₂ = Sґ₂(S₂) (рис.6.18), которую строим следующим образом.

По оси ординат графика Sґ₂ = Sґ₂(S₂) откладываем перемещение точки А толкателя в масштабе m_l в соответствии с заданным законом движения. По оси абсцисс откладываем отрезки A_iD_i, изображающие в масштабе m_l аналоги скоростей. Для определения направления, в котором надо откладывать отрезки A_iD_i от точки А, надо аналог скорости в соответствующем положении повернуть на 90° по вращению кулачка. Соединяя полученные точки D_i плавной кривой, получаем диаграмму аналога скорости толкателя.

Чтобы угол давления ни в одном из положений механизма не превышал n_доп., необходимо центр вращения кулачка расположить в зоне, ограниченной касательными t₁ - t₁ и t₂ - t₂, проведенными под углом n_доп. к оси толкателя. При выборе центра в точке О₁ получим наименьший начальный радиус (О₁А₀) и вполне определенную величину смещения е₁. Габариты кулачка получаются наименьшими: R_0min = (О₁А₀)m_l.

При заданном смещении е, на диаграмме проводится прямая I-I, параллельная траектории движения центра ролика, и отстоящая от нее с заданной стороны на расстоянии, равном величине смещения е в масштабе m_l. Тогда центр вращения кулачка определится как пересечение прямых I-I с t₂ - t₂ и будет равен R₀ = (О₂А₀) m_l [м].

Рис.6.19

Рис.6.18