Теорема о достаточности четырех функций.

Из любой полной в Р₂ системы функций можно выделить полную подсистему, состоящую не более чем из четырех функций.

Доказательство. Пусть {f₀, f₁, f_L, f_M, f_S} – полная система функций, тогда она не лежит целиком ни в одном из классов T₀, T₁, L, M, S. Следовательно, в системе есть функции f₀ÏT₀, f₁ÏT₁, f_LÏL, f_S ÏS и f_mÏM. Система {f₀, f₁, f_L, f_M, f_S} Í P₂ и образует полную систему в Р₂. Рассмотрим функцию f₀: f₀(0, ..., 0) = 1.

Если f₀(1, ..., 1) = 0, то f₀ÏT₁ и f₀ÏM, тогда {f₀, f_S, f_L} – полная система из трех функций.

Если f₀(1, ..., 1) = 1, то f₀ÏS и {f₀, f₁, f_L, f_M } образует полную систему из четырех функций.

Пример 1, приведенный выше, показывает, что цифру 4 в общем случае уменьшить нельзя, из полной системы {x₁x₂,0,1,x₁Åx₂Åx₃} нельзя выделить полную подсистему.

Следствие. Базис в Р₂ может состоять максимум из четырех функций.

 

2.7. Функции k - значной логики

Введем обозначение: E_к={0, 1, 2, ..., k–1}.

Функция k-значной логики, зависящая от n переменных, – это закон, отображающий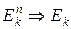. Множество функций k-значной логики обозначается как Р_k. Функция из Р_k полностью определена, если задана ее таблица истинности, т.е. заданы значения на всех наборах. Наборы можно рассматривать как записи в k-ичной системе счисления чисел от 0 до k–1, всего наборов kⁿ. Функций из Р_k, зависящих от n переменных, будет kⁿ. |P₃(n)|, например, будет 3, если n = 2, то |P₃(2)| = 3⁹ = 19683 (k=3, n=2).

x1 x2 . . . xn-1 xn	f
0 0 . . . 0 0 0 0 . . . 0 1 . . . . . . . . . . . . . . . . . . . 0 0 . . . 0 k–1 0 0 . . . 1 0 . . . . . . . . . . . . . . . . . . . k–1 k–1 . . . k–1 k–1	. . . . . . .

В k - значной логике также есть функции, которые называются элементарными. Приведем некоторые из них, примеры будем приводить для k = 3 и n = 2.

1. Циклический сдвиг или отрицание Поста: = x+1(mod k).

2. Зеркальное отображение или отрицание Лукосевича: N_x = k–1–x.

Эти две функции являются обобщением отрицания.

3. J_i(x)={k-1, x = i, I = 0, 1, 2, ..., k–1}.

 

x1	x2	Nx	J0(x)	J1(x)	J2(x)

4. min(x₁,x₂) – обобщение конъюнкции;

5. x₁×x₂(mod k) – второе обобщение конъюнкции;

6. max(x₁,x₂) – обобщение дизъюнкции;

7. x₁+x₂(mod k) – сумма по mod k.

x1	x2	min(x1,x2)	x1x2(mod 3)	max(x1x2)	x1+x2(mod 3)

Принято min(x₁,x₂) обозначать x₁&x₂, max(x₁,x₂) обозначать x₁Úx₂.

Как и в двузначной логике, можно ввести понятие формулы над множеством и ставить вопрос о полной в Р_k системе функций.

Теорема о полной в Р_k системе функций

Cистема функций {max(x₁,x₂), min(x₁,x₂), 0, 1, ..., k–1, J₀(x), J₁(x), ..., J_k-1(x)} является полной в Р_k и любая функция f(x₁, ..., x_n) Î P_k выражается формулой над этой системой следующим образом:

.

Эта формула есть своеобразный аналог СДНФ.

Доказательство. Покажем справедливость этой формулы на любом произвольном наборе (a₁, ..., a_n). Слева имеем f(a₁, ..., a_n). Справа имеем .

Если для какого-нибудь j из {1, 2, ..., n} i_j ¹ a_j, то (a_j) = 0 и min[J(a₁), (a₂), …, (a_n), f(i₁,..,i_n)] = 0. Рассмотрим набор (i₁, ..., i_n), где i₁ = a₁, i₂ = a₂, ..., i_n = a_n, тогда J(a₁) = k–1, J(a₂) = k–1, .., J(a_n) = k–1 и min[J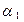(a₁), ... , J(a_n) f(a₁, …, a_n).] = min[(k–1), ..., (k–1), f(a₁, …, a_n).] = f(a₁, …, a_n), но тогда 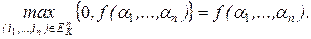Так как набор (a₁, ..., a_n) произвольный и равенство на нем справедливо, то формула верна. В этой формуле использованы функции J_i(x), (i = 0, ..., k–1), min(x₁x₂), max(x₁x₂) и константы 0, ..., k–1, так как функция f(i₁, ..., i_n) есть число из {0, 1, ..., k–1}.