рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- УСМАНОВА Зинира Масгутовна
Реферат Курсовая Конспект
УСМАНОВА Зинира Масгутовна
УСМАНОВА Зинира Масгутовна - раздел Образование, Ахметова Наиля Абдулхамито...
АХМЕТОВА Наиля Абдулхамитовна
УСМАНОВА Зинира Масгутовна
Дискретная математика Функции алгебры логикиРедакционно – издательский комплекс УГАТУ
СодержаниеЗамыкание и замкнутые классы ………………………………….. 48
Функции k – значной логики ……………………………………55
2.8. Задачи и упражнения по функциям алгебры логики....................... 58
3. Минимизация булевых функций .......................................................... 80
3.1. Минимизация нормальных форм …………………………………80
3.2. Минимизация частично определенных функций ………………… 93
3.3. Задачи по минимизации и доопределению булевых функций……102
4. Логика высказываний ……………………………………………… 106
4.1. Введение в логику высказываний ……………………………… 106
4.2. Задачи по алгебре высказываний ………………………………… 117
Список литературы .............................................................................. 126
ВВЕДЕНИЕ
Дискретная математика – часть математики, которая зародилась в глубокой древности. В широком смысле этого слова к дискретной математике относятся как классические разделы математики: алгебра, теория чисел, теория множеств, математическая логика и т.д., так и новые разделы, которые возникли в середине нашего столетия в связи с внедрением ЭВМ в практическую жизнь. В узком смысле, а в настоящее время именно в узком смысле слова «дискретная математика» и употребляются, сюда относят только те разделы, которые связаны с анализом сложных управляющих систем.
Курс дискретной математики, входящий в программу для ряда специальностей УГАТУ, включает в себя функции алгебры двузначной и к-значной логики, автоматные функции, теорию графов, теорию кодирования, синтез схем из функциональных элементов, элементы комбинаторики и алгебру высказываний.
В этом пособии будут рассмотрены элементы комбинаторики, функции двузначной и к-значной логики и логика высказываний.
При этом будет использован формализм, который оказался особо подходящим для строгого описания многих разделов компьютерной математики – булева алгебра. Булева алгебра содержит в себе основные положения элементарной логики. Примерами булевой алгебры являются алгебра множеств и алгебра высказываний. Название связано с именем английского математика Джорджа Буля (1815 – 1864). Полное формальное представление булевой алгебры было дано лишь в 1904 году Хантингтоном. Он ввел систему аксиом, из которых могут быть выведены все утверждения булевой алгебры. Предпошлем основному изложению определение булевой алгебры.
Алгеброй Буля называется произвольное множество элементов {a, b, ...}, для которых определены две бинарные операции, условно называемые «сложение» и «умножение», которые каждым двум элементам a и b ставят в соответствие третий, и одна унарная операция, условно называемая «черта», которая каждому элементу ставит в соответствие другой. В этом множестве имеются два особых элемента, назовем их 0 и e, и выполняются cледующие правила:
1) коммутативность сложения и умножения;
2) ассоциативность сложения и умножения;
3) дистрибутивность умножения относительно сложения и наоборот;
4) идемпотентность: a+a=a и a a=a ;
a=a ;
5) инволюция  =a;
=a;
6) правила де Моргана:  ,
,  ;
;
7)  =e и
=e и  =0;
=0;
8) a+0=a , a+e=e , a 0=0 , a
0=0 , a e=a.
e=a.
Определение булевой алгебры, кажущееся с первого взгляда громоздким и весьма специальным, на самом деле явилось результатом глубокого проникновения в существо многих внешне не схожих явлений и прoцессов, абстрактное описание которых позволило обнаружить далеко идущие аналогии.
Например, алгебру Буля образует множество подмножеств любого множества (универсума), где в качестве бинарных операцией взяты пересечение(Ç) и объединение ( È) множеств, в роли особого элемента 0 служит пустое множество Æ, а в роли e - сам универсум, в роли операции отрицания – дополнение.
Пособие состоит из четырех разделов. В первом разделе излагаются элементы комбинаторики, причем в таком объеме, который позволяет обеспечить приемлемую строгость изложения в последующих разделах, например, при оценке мощностей замкнутых классов.
Во втором разделе рассматриваются основные положения алгебры логики. Здесь особую роль играет множество {0,1}, элементы которого не являются числами в обычном смысле, хотя по некоторым свойствам и похожи на них. Наиболее распространенная интерпретация двоичных переменных – логическая: «да» – «нет», «истинно» (и) – «ложно» (л). В контексте, содержащем одновременно двоичные и арифметические величины и функции, эта интерпретация обычно фиксируется явно, например, в языках программирования. В данном пособии логическая интерпретация двоичных переменных необходима только в разделе, посвящённом логике высказываний.
Третий раздел содержит методы минимизации булевых функций. Знание этих методов полезно при изучении, например, таких разделов дискретной математики, как «схемы из функциональных элементов» – для понижения сложности схем, и «автоматные функции» – для доопределения частично определённых функций.
В четвёртом разделе приведены элементы логики высказываний – булевой алгебры на множестве {истина, ложь}.
Каждый раздел пособия содержит теоретический материал, сопровождаемый большим числом примеров, и завершается задачами для самостоятельного решения. Причём количество задач таково, что пособие может быть использовано преподавателями на практических занятиях.
Работа выполнена на кафедре математики УГАТУ. Учебное пособие написано по материалам лекций и практических занятий по курсу дискретной математики, которые проводили авторы.
1. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Перестановки. Размещения. Сочетания
Пусть есть некоторое конечное множество элементов U={a1, a2, ..., an}. Рассмотрим набор элементов , где ÎU, j = 1, 2, ..., r. Этот набор называется выборкой объема r из n элементов. Любое подмножество U… Комбинаторные задачи связаны с подсчетом числа выборок объема r из n элементов, где выборки подчиняются определенным…ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
Элементарные функции алгебры логики
Определение 1. Функцией алгебры логики называется закон, осуществляющий отображение ЕE2, причем отображение всюду определено и функционально. Так как множество Еконечно, то задать отображение ЕÞ E2, означает задать… Пример 1. Пусть n=2, тогда Е={(0 0),(0 1),(1 0),(1 1)}, отображение ЕÞ E2 задано, например, так: (0 0) Þ0…Пример 2.
Рассмотрим несколько функций двух переменных
| x1 | x2 | (x1&x2) | f3 | f15 |
Покажем, что (х1&x2) существенно зависит от х1. Рассмотрим наборы (0,1) и (1,1), здесь a2=1, f(0,a2)=0 и не равно f(1,a2)=1. Покажем, что х2 тоже существенная переменная. Рассмотрим наборы (1,0) и (1,1). Здесь a1=1, f(1,0)=0 и не равно f(1,1)=1. Для функции f3(x1,x2) покажем , что х2 – иктивная переменная, т.е. надо показать, что не существует наборов (a1,0) и (a1,1) таких, что f3(a1,0)¹f3(a1,1). Пусть a1=0, т.е. рассмотрим наборы (0,0) и (0,1), f(0,0)=f(0,1)=0. Пусть a1=1, но f(1,0)=f(1,1)=1.
Для функции f15 и x1 и x2 являются фиктивными переменными. x1 – фиктивная переменная, если не существует наборов (0,a2) и (1,a2), таких, что f(0,a2)¹f(1,a2). Если a2=0, то f(0,0)=f(1,0)=1. Пусть a2=1, тогда f(0,1)=f(1,1)=1.
Пусть хi является фиктивной переменной для функции f(x1, ..., xi, ..., xn). Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида: (a1, ...ai–1, 1, ai+1, ...an) или, наоборот, все строки вида: (a1, ..., ai–1, 0, ai+1, ...an) и столбец для переменной хi. При этом получим таблицу для некоторой функции g(x1, ..., xi–1, xi+1, ...xn). Будем говорить, что функция g(x1, ...xi–1, xi+1, ...xn) получена из функции f(x1, ..., xi, ...xn) путем удаления фиктивной переменной хi или f получена из g путем введения фиктивной переменной хi.
Определение 4. Функции f1 и f2 называются равными, если f2 можно получить из f1 путем добавления или удаления фиктивной переменной.
Пример 3.
| x1 | x2 | f3 |
Вычеркнули строки типа (a,1), т.е. (0,1) и (1,1) и столбец для х2.
Получили f3(x1 x2) = g(x1) = x1.
Пример 4.
| x1 | x2 | g |
Пусть функция g(x1 x2) задана таблицей и существенно зависит от обеих переменных. Построим функцию f(x1,x2,x3), которая получается из g(x1,x2) введением фиктивной переменной х3:
| x1 | x2 | x3 | f |
К наборам (х1,х2) мы добавим х3=0, получим наборы вида: (a1,a2,0), на этих наборах функцию f положим равной g(a1,a2), затем добавим наборы вида (a1,a2,1), функцию f(a1,a2,1) положим равной g(a1,a2).
Особую роль играют константы 0 и 1, которые не имеют существенных переменных и которые можно рассматривать как функции от пустого множества переменных.
Формульное задание функций алгебры логики
Дадим индуктивное определение формулы над множеством. Это определение несколько сложное по форме, но будет полезно в дальнейшем. С индуктивным определением мы встречались в математическом анализе при определении n-го дифференциала dnf(x) : было введено понятие первого дифференциала df(x), а затем n-й дифференциал определялся как первый дифференциал от d(n–1)f(x).
Определение 1. Пусть МÌP2, тогда:
1) каждая функция f(x1, ..., xn)Î M называется формулой над M;
2) пусть g(x1, ..., xm)ÎM , G1, ..., Gm – либо переменные, либо формулы над M. Тогда выражение g(G1...Gn) – формула над M .
Формулы будем обозначать заглавными буквами: N[f1, ..., fs], имея в виду функции, участвовавшие в построении формулы, или N(х1, ..., xk) имея в виду переменные, вошедшие в формулу. Gi – формулы, участвовавшие в построении g(G1, ..., Gn), называются подформулами.
Пример 1. Пусть N={(x1&x2),(x1Úx2),(`x )}, тогда ((х1&х2)Úх3) – формула над N.
Сопоставим каждой формуле N(x1, ..., xn) функцию f(x1, ..., xn)ÎP2. Сопоставление будем производить в соответствии с индуктивным определением формулы.
1) Пусть N(x1, ..., xn)=f(x1, ..., xn), тогда формуле N(x1, ..., xn) сопоставим функцию f(x1, ..., xn).
2) Пусть N(x1, ..., xn)=g(G1, ..., Gm), где каждое Gi – либо формула над M, либо переменная, тогда по индуктивному предположению каждому Gi сопоставлена либо функция fiÎP2 , либо переменная хi , которую можно считать тождественной функцией. Таким образом, каждой формуле Gi сопоставлена функция fi( ), причем:{
), причем:{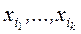 }Í{x1, ..., xn}, т.к. в формуле N(x1, ..., xn) перечислены все переменные, участвовавшие в построении формулы. Можно считать, что все функции fi зависят от переменных (x1, ..., xn), причем какие-то переменные могут быть фиктивными. Тогда N(x1, ..., xn) = g(G1, ..., Gm) = g( f1(x1, ..., xn), ..., fm(x1,..,xn)). Сопоставим этой формуле функцию h(x1, ..., xn) следующим образом: пусть (a1, ..., an) – произвольный набор переменных (x1, ..., xn). Вычислим значение каждой функции fi на этом наборе, пусть f(a1, ..., an)=bi, затем найдем значение функции g(x1, ..., xm) на наборе (b1, ..., bm) и положим h(a1, ..., an) = g(b1, ..., bm) = g(f1(a1, ..., an), ..., fm(a1, ..., an)). Так как каждое fi(x1, ..., xn) есть функция, то на любом наборе (a1, ..., an) она определяется однозначно, g(x1, ..., xm) – тоже функция, следовательно, на наборе (b1, ..., bn) она определяется однозначно, где h(x1, ..., xn) есть функция, определенная на любом наборе (a1, ..., an).
}Í{x1, ..., xn}, т.к. в формуле N(x1, ..., xn) перечислены все переменные, участвовавшие в построении формулы. Можно считать, что все функции fi зависят от переменных (x1, ..., xn), причем какие-то переменные могут быть фиктивными. Тогда N(x1, ..., xn) = g(G1, ..., Gm) = g( f1(x1, ..., xn), ..., fm(x1,..,xn)). Сопоставим этой формуле функцию h(x1, ..., xn) следующим образом: пусть (a1, ..., an) – произвольный набор переменных (x1, ..., xn). Вычислим значение каждой функции fi на этом наборе, пусть f(a1, ..., an)=bi, затем найдем значение функции g(x1, ..., xm) на наборе (b1, ..., bm) и положим h(a1, ..., an) = g(b1, ..., bm) = g(f1(a1, ..., an), ..., fm(a1, ..., an)). Так как каждое fi(x1, ..., xn) есть функция, то на любом наборе (a1, ..., an) она определяется однозначно, g(x1, ..., xm) – тоже функция, следовательно, на наборе (b1, ..., bn) она определяется однозначно, где h(x1, ..., xn) есть функция, определенная на любом наборе (a1, ..., an).
Множество всех формул над M обозначим через <M>.
Определение 2. Две формулы N и D из <M> называются равными N=D или эквивалентными N~D , если функции, реализуемые ими, равны.
Пример 2.Доказать эквивалентность формул:
( &(х2Åx3))~(
&(х2Åx3))~(  ) .
) .
| x1 | x2 | x3 | x2Åx3 | & | x2 x3 x3
| x3 x2 x2
| & | Úx1 | 
|
Упрощение записи формул:
1) внешние скобки можно отпускать;
2) приоритет применения связок возрастает в следующем порядке: ~, , Ú,&;
, Ú,&;
3) связка – над одной переменной сильнее всех связок;
4) если связка – стоит над формулой, то сначала выполняется формула, затем отрицание;
5) если нет скобок, то операции ~ и  выполняются в последнюю очередь.
выполняются в последнюю очередь.
Теорема о замене подформул на эквивалентные
Пусть NÎ<M> и имеет вид: N(x1, ..., xn) = g(G1, ...Gi, ...,Gm). Пусть подформула Gi~Gi¢, тогда формула N(x1, ..., xn) = g(G1,… Доказательство. Формулы N и N¢ эквивалентны, если реализуют одну и ту же… N(x1, ..., xn) = g(f1(x1, ..., xn ), ..., fi(x1, ..., xn), ..., fm(x1, ..., xn)),Некоторые свойства элементарных функций
1. Идемпотентность & и Ú: х&x=x , xÚx=x. 2. Коммутативность &,Ú,Å,|,~,. 3. Ассоциативность &,Ú,Å,~, поэтому в формулах вида xyz можно не ставить никаких скобок.Принцип двойственности
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1: x f f* … Функции f(x) = x и g(x) = двойственны сами себе: x f f* g g* …Пример 3. Покажем, что функция х1Úх2 двойственна к x1&x2, функция х1х2 двойственна к функции x1|x2.
| x1 x2 | f=х1Úх2 | f* | g=x1|x2 | g*=x1 x2 x2
|
| 0 0 0 1 1 0 1 1 |
Теорема о двойственных функциях
Если f* двойственна к f, то f двойственна к f*.
Доказательство. f*(x1, ..., xn) =  (
( 1, ...,
1, ...,  n). Найдем двойственную функцию к f*, т.е. (f*( x1, ..., xn))* = (
n). Найдем двойственную функцию к f*, т.е. (f*( x1, ..., xn))* = ( (
( 1, ...,
1, ...,  n))* =
n))* =  (
( 1, ...,
1, ..., 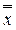 n) = f(x1, .., xn).
n) = f(x1, .., xn).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Принцип двойственности
Доказательство. h*(x1, ..., xn) = (1, ..., n) = (f1(1, ..., n), ..., fm(1, ..., n)) = (1(1, ..., n), ..., (1, ..., n)) = g((), ..., (() = g*(f1*(… Если функция h(x1, ..., xn) реализуется формулой N[f1, ..., fn], то формулу,… Пример 4. Построить формулу, реализующую f*, если f = ((xy) Ú z) (y(xÅyz)). Покажем, что она эквивалентна…Лемма о несамодвойственной функции
Подстановкой функций и в несамодвойственную функцию можно получить одну из констант. Доказательство.Пусть – несамодвойственная функция. Тогда существует набор ,… Тогда , т.е. . Следовательно, функция есть одна из констант.Разложение булевой функции по переменным
Посмотрим, чему равно xs при разных значениях x и s. xs … Из таблицы следует: xs=1 тогда и только тогда, когда x=s.Теорема о разложении функции по переменным
Пусть f(x1, ..., xn) Î P2. Тогда для любого m: 1 ≤ m ≤ n допустимо представление: f(x1, ..., xm, xm+1, ..., xn) = , где дизъюнкция берется по всем наборам из 0 и 1, которое называется разложением функции f по переменным x1, ..., xn. …Следствие 1. Любую функцию f(x1, ..., xn) не равную тождественно нулю можно представить в виде: , причём единственным образом. Этот вид называется совершенной дизъюнктивной нормальной формой функции f(x1, ..., xn) и записывается СДНФ.
Доказательство.Существование СДНФ для функции не равной тождественно нулю вытекает из предыдущей теоремы. Покажем, что эта СДНФ единственная. В самом деле, имеется 
 n-местных функций, не равных нулю тождественно. Подсчитаем число различных СДНФ от n переменных. Путь
n-местных функций, не равных нулю тождественно. Подсчитаем число различных СДНФ от n переменных. Путь  означает число сочетаний из n элементов по k. Тогда число одночленных СДНФ
означает число сочетаний из n элементов по k. Тогда число одночленных СДНФ 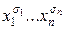
 равно
равно  . Число k-членных СДНФ равно
. Число k-членных СДНФ равно 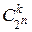 . Число n-членных СДНФ равно
. Число n-членных СДНФ равно  . Число всех различных СДНФ
. Число всех различных СДНФ 
Итак,  функций реализуются посредством
функций реализуются посредством  СДНФ, т.е. каждой функции соответствует единственная СДНФ.
СДНФ, т.е. каждой функции соответствует единственная СДНФ.
Замечание.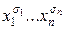 – элементарная конъюнкция ранга n по числу входящих переменных, предполагается, что при i ¹ j , хi ¹ хj. СДНФ для f(x1, ..., xn) –дизъюнкция элементарных конъюнкций ранга n. Если функция представлена в виде дизъюнкций элементарных конъюнкций, где ранг хотя бы одной элементарной конъюнкции меньше n, то такая форма называется дизъюнктивной нормальной формой (ДНФ).
– элементарная конъюнкция ранга n по числу входящих переменных, предполагается, что при i ¹ j , хi ¹ хj. СДНФ для f(x1, ..., xn) –дизъюнкция элементарных конъюнкций ранга n. Если функция представлена в виде дизъюнкций элементарных конъюнкций, где ранг хотя бы одной элементарной конъюнкции меньше n, то такая форма называется дизъюнктивной нормальной формой (ДНФ).
Cледствие 2. Любая функция алгебры логики может быть представлена в виде формулы через отрицание, & и Ú.
а) Если f ≡ 0, то f(x1, ..., xn) =  &
& .
.
б) Если f(x1, ..., xn) ¹ 0 тождественно, тогда ее можно представить в виде СДНФ, где используются только связки  , &, Ú. СДНФ дает алгоритм представления функции в виде формулы через &, Ú,
, &, Ú. СДНФ дает алгоритм представления функции в виде формулы через &, Ú,  .
.
Пример 3. Пусть функция f(x1, x2, x3) задана таблицей истинности. Запишем ее в виде СДНФ. Наборов, на которых функция равна 1, три: (0, 1, 0), (1, 0, 0) и
(1, 1, 1), поэтому f(x1, x2, x3) = x10 & x21 & x30 Úx11 & x20 & x30 Úx11&x21 & x31=
= &x2&
&x2& Úx1&
Úx1& &
& Úx1&x2&x3.
Úx1&x2&x3.
| x1 | x2 | x3 | f | ||||

Следствие 3. Мы умеем представлять функцию в виде 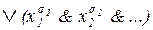 . Нельзя ли представить ее в виде
. Нельзя ли представить ее в виде  . Пусть функция f(x1, ..., xn) ¹ 1 тождественно. Тогда функция f* ¹ 0 тождественно, и ее можно представить в виде СДНФ:
. Пусть функция f(x1, ..., xn) ¹ 1 тождественно. Тогда функция f* ¹ 0 тождественно, и ее можно представить в виде СДНФ:
 .
.
По принципу двойственности заменим & на Ú и наоборот, получим
 (2)
(2)
 называется элементарной дизъюнкцией ранга n. Представление функции в виде (2) называется совершенной конъюнктивной нормальной формойили в краткой записи – СКНФ. СКНФ для f(x1, ..., xn) – конъюнкция элементарных дизъюнкций ранга n. КНФ для f(x1, ..., xn) – конъюнкция элементарных дизъюнкций, где ранг хотя бы одной элементарной дизъюнкции меньше n.
называется элементарной дизъюнкцией ранга n. Представление функции в виде (2) называется совершенной конъюнктивной нормальной формойили в краткой записи – СКНФ. СКНФ для f(x1, ..., xn) – конъюнкция элементарных дизъюнкций ранга n. КНФ для f(x1, ..., xn) – конъюнкция элементарных дизъюнкций, где ранг хотя бы одной элементарной дизъюнкции меньше n.
Пример 4. Пусть f(x1, x2, x3) = x1  (x2
(x2 (x3 ~ x1)). Представим ее в виде СКНФ, для этого получим таблицу истинности.
(x3 ~ x1)). Представим ее в виде СКНФ, для этого получим таблицу истинности.
| x1 | x2 | x3 | x3~x1 |  x2 x2 (x3~x1) (x3~x1)
| f |
| 1 | 1 | 1 | 1 1 | 1 | 1 |
Функция равна нулю только на наборе (1, 1, 0), поэтому
f(x1 x2 x3)=x1 Úx2
Úx2 Úx3
Úx3 =x10Úx20Úx31=
=x10Úx20Úx31= Ú
Ú Ú x3.
Ú x3.
Полнота, примеры полных систем
Определение. Система функций {f1, f2, ..., fs, ...}ÌP2 называется полной в Р2, если любая функция f(x1, ..., xn) Î P2 может быть записана в виде формулы через функции этой системы.
Полные системы
2. Система M={x1&x2, x1Úx2, } – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции. … Пример 1. Неполные системы: {}, {0,1}.Доказательство. Пусть h(x1, ..., xn) Î P2, т.к. U полна в Р2, то h(x1, ..., xn) = =N[f1, ..., fs, ...] = N[L1[g1, ..., gk], ..., Ls[g1, ..., gk], ...] = U[g1, ..., gk]. Здесь мы воспользовались тем, что для любого i n fi может быть выражена формулой над B, поэтому fi=Li[gi, ..., gk].
3. Система {x1Úx2,  } – полна в P2.
} – полна в P2.
Возьмем в качестве полной в Р2 системы U={x1Úx2,  , x1&x2}, B={x1Úx2,
, x1&x2}, B={x1Úx2,  }. Надо показать, что x1&x2 представляется формулой над B. Действительно, по правилу Де Моргана получим: x1&x2=
}. Надо показать, что x1&x2 представляется формулой над B. Действительно, по правилу Де Моргана получим: x1&x2= .
.
С помощью этой леммы докажем полноту еще ряда систем.
4. Система {x1&x2,  } – полна в Р2.
} – полна в Р2.
5. Система {x1|x2} полна в Р2. Для доказательства возьмем в качестве полной в Р2 системы U = {x1&x2,  } и выразим х1&х2 и
} и выразим х1&х2 и  через х1|x2 :
через х1|x2 :
 = x1 | x1, x1 & x2 =
= x1 | x1, x1 & x2 = = (x1|x2)|(x1|x2).
= (x1|x2)|(x1|x2).
6. Система {x1 x2} полна в Р2. U = {x1Úx2,
x2} полна в Р2. U = {x1Úx2, 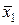 },
},  = x1
= x1 x1, x1Úx2 =
x1, x1Úx2 =  = (x1
= (x1 x2)
x2)  (x1
(x1 x2).
x2).
7. Система {x1&x2, x1Åx2, 0, 1}, U = {x1&x2,  },
},  = x1Å1.
= x1Å1.
Следствие. Полином Жегалкина.
f(x1, ..., xn) Î P2, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как {x1&x2, x1Åx2, 0, 1} полна в Р2. В силу свойства x & (yÅz) = xy Å xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х х
х ...х
...х , соединенных знаком Å. Такой полином называется полиномом Жегалкина.
, соединенных знаком Å. Такой полином называется полиномом Жегалкина.
Общий вид полинома Жегалкина:

где 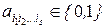 , s = 0, 1, ..., n, причем при s = 0 получаем свободный член а0.
, s = 0, 1, ..., n, причем при s = 0 получаем свободный член а0.
Представление функции в виде полинома Жегалкина
1. Представим любую функцию формулой над {x1&x2, } и сделаем замену
} и сделаем замену  =xÅ1. Этот способ удобен, если функция задана формулой.
=xÅ1. Этот способ удобен, если функция задана формулой.
Пример 2. (x1 (x2
(x2 x3))(x1 Ú x2) x3 = (x1Ú x2 Ú x3)(x1 Ú x2) x3 = (`x1x2 Ú x1x3 Ú x1x2 Ú x2 Ú x2x3)x3 = (`x1x3 Ú x2)x3 = x1x3 x2 x3 = ((x1x3Å1)x2Å1)x3 = x1x2x3Åx2x3Åx3.
x3))(x1 Ú x2) x3 = (x1Ú x2 Ú x3)(x1 Ú x2) x3 = (`x1x2 Ú x1x3 Ú x1x2 Ú x2 Ú x2x3)x3 = (`x1x3 Ú x2)x3 = x1x3 x2 x3 = ((x1x3Å1)x2Å1)x3 = x1x2x3Åx2x3Åx3.
Надо помнить, что четное число одинаковых слагаемых в сумме по mod2 дает 0.
2. Метод неопределенных коэффициентов. Он удобен, если функция задана таблицей.
Пример 3. Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных f(x1, x2, x3) = (01101001) = а0 Å а1х1Å Å а2х2 Å а3х3 Å b1x1x2 Å b2x2x3 Å b3x1x3 Å cx1x2x3. Затем находим коэффициенты, используя значения функции на всех наборах. На наборе (0, 0, 0) f(0, 0, 0) = 0, с другой стороны, подставив этот набор в полином, получим f(0, 0, 0) = а0, отсюда а0 = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим: f(0, 0, 1) = а0 Å а3, т.к. а0 = 0, отсюда а3 = 1. Аналогично, f(0, 1, 0) = 1 = а2, f(0, 1, 1) = 0 = а2 Å а3 Å b2 = b2 = 0; а1 = 1; 0 = а1 Å а3 Å b3 = b3 = 0; 0 = а1 Å а2 Å b1 = b1 = 0; 1 = 1 Å 1 Å 1 Å c; c = 0; f(x1, x2, x3) = x1 Å x2 Å x3.
3. Многочлен Жегалкина можно получить также с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом. Построим многочлен Жегалкина для функции f = (10011110). Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответсвует набору (101). В качестве слагаемого многочлена берем x1x3. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
| N | x1x2x3 | f | Треугольник Паскаля | |||||
| x3 x2 x2x3 x1 x1x3 x1x2 x1x2x3 | 1 0 0 1 1 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 1 0 | |||||||
Тогда 
Теорема Жегалкина
Каждая функция из может быть представлена в виде полинома Жегалкина единственным образом. Здесь единственность понимается с точностью до порядка слагаемых в сумме и… , s = 0, 1, ..., n. Доказательство. Любая функция из Р2 может быть представлена формулой над {x1 & x2, x1Å…Т0 - класс функций, сохраняющих константу 0.
Т0 = { f(x1, ..., xn | f(0, ..., 0) = 0, n = 1, 2, ...}. Покажем, что Т0 является собственным подмножеством Р2, т.е. Т0 ¹ Æ и Т0 Ì Р (не совпадает с Р2). Для этого достаточно привести примеры функций, входящих в Т0, и примеры функций из Р2, не входящих в Т0: x1&x2, x1Úx2, xÎТ0 и x1|x2, x1 x2,
x2,  ÏТ0. Покажем далее, что [Т0] = Т0. Вложение Т0 Í [ Т0] очевидно, так как по определению формулы любая функция из Т0 является формулой над Т0 и, следовательно, принадлежит [Т0]. Покажем, что [Т0]Í Т0. Для этого надо показать, что Ф = f(f1, ..., fm) Î [ Т0], если все функции f, f1, f2, f3, ..., fm Î Т0. Надо заметить, что в формуле в качестве функции f1 могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т0, поэтому достаточно показать, что Ф = f (f 1, ..., fm) Î Т0. Для этого рассмотрим следующую функцию: Ф(0, ..., 0) = f (f 1(0, ..., 0), f 2(0, ..., 0), ...) = f(0, ..., 0) = 0.
ÏТ0. Покажем далее, что [Т0] = Т0. Вложение Т0 Í [ Т0] очевидно, так как по определению формулы любая функция из Т0 является формулой над Т0 и, следовательно, принадлежит [Т0]. Покажем, что [Т0]Í Т0. Для этого надо показать, что Ф = f(f1, ..., fm) Î [ Т0], если все функции f, f1, f2, f3, ..., fm Î Т0. Надо заметить, что в формуле в качестве функции f1 могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т0, поэтому достаточно показать, что Ф = f (f 1, ..., fm) Î Т0. Для этого рассмотрим следующую функцию: Ф(0, ..., 0) = f (f 1(0, ..., 0), f 2(0, ..., 0), ...) = f(0, ..., 0) = 0.
Число функций, зависящих от n переменных и принадлежащих Т0, будет равно 

2) T1 – класс функций, сохраняющих константу 1.
T1 = {f(x1, ...) |f(1, 1, ...) = 1}; x1&x2, x1Úx2, xÎT1, х1Åх2, x1 x2ÏT1, следовательно Т1 – собственное подмножество Р2.
x2ÏT1, следовательно Т1 – собственное подмножество Р2. 
Покажем, что [T1] Í T1, обратное включение следует из определения формулы и замыкания. Так как тождественная функция входит в Т1, можно рассмотреть Ф = f(f1, ..., fn) Î [T1], где f, f1, ..., fn Î T1. Найдем Ф(1, ..., 1) = f(f1(1, ..., 1), ..., fn(1, ..., 1)) = f(1, ..., 1) = 1, следовательно, Ф = f(f1, ..., fn) Î T1, отсюда следует [T1] = T1.
S – класс самодвойственных функций.
S = {f(x1, ...)|f* = f }; x,  , x1Åx2Åx3ÎS, x1&x2, x1Úx2, x1Åx2ÏS, следовательно, S – собственное подмножество Р2. |S(n)| =
, x1Åx2Åx3ÎS, x1&x2, x1Úx2, x1Åx2ÏS, следовательно, S – собственное подмножество Р2. |S(n)| =  . Покажем, что [S]ÍS. Ф = f(f1, ..., fn) Î [S], если f, f1, ..., fn Î S, а также, что Ф Î S. По принципу двойственности, Ф* = f*(f1*, ..., fn*) = f(f1, ..., fn) = Ф, отсюда S – замкнутый класс.
. Покажем, что [S]ÍS. Ф = f(f1, ..., fn) Î [S], если f, f1, ..., fn Î S, а также, что Ф Î S. По принципу двойственности, Ф* = f*(f1*, ..., fn*) = f(f1, ..., fn) = Ф, отсюда S – замкнутый класс.
L – класс линейных функций.
L = {f(x1, ...)| f = c0Åc1x1Å...Åcnxn}; очевидно, L ¹ Æ, с другой стороны
L ¹ P2, так как x1&x2 Ï L. Заметим, что тождественная функция принадлежит L и |L(n)| = 2n+1. Покажем, что [L] Í L. Рассмотрим Ф = f(f1, ..., fm), где f, f1, ..., fn Î L. Тогда Ф = а0 Å а1(с10 Å с11х1 Å...Å c1nxn1) Å a2(c20 Å c21x1 Å c22x2Å ...Å c2nxn2)Å...Å an(cm0 Åcm1x1 Å ... Å cmnxnm) = в0 Å в1х1 Å ...Å вnхn Þ ФÎL.
5) М – класс монотонных функций.
Определение. Набор 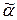 = (a1, ..., an) предшествует набору
= (a1, ..., an) предшествует набору  = (b1, ..., bn) и обозначается
= (b1, ..., bn) и обозначается  , если для 1£i£n ai£bi, например:
, если для 1£i£n ai£bi, например: 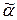 = (0010),
= (0010),  = (0110), тогда
= (0110), тогда 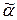

 . Не любые два набора находятся в отношении предшествования, например, наборы (0110) и (1010) в таком отношении не находятся. Отношение предшествования (
. Не любые два набора находятся в отношении предшествования, например, наборы (0110) и (1010) в таком отношении не находятся. Отношение предшествования ( ) является отношением порядка на множестве наборов длины n, множество таких наборов будет частично упорядоченным множеством по отношению к операции.
) является отношением порядка на множестве наборов длины n, множество таких наборов будет частично упорядоченным множеством по отношению к операции.
Определение. Функция f(x1, ..., xn) называется монотонной, если для двух наборов 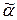 и
и  , таких что
, таких что 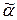

 , выполняется f(
, выполняется f(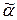 )
) f(
f( ). Функции 0, 1, x, x1&x2, x1 Ú x2 Î M, x1¯x2, x1 Å x2, x1 ~ x2 Ï M.
). Функции 0, 1, x, x1&x2, x1 Ú x2 Î M, x1¯x2, x1 Å x2, x1 ~ x2 Ï M.
Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число сосчитать не удается. Покажем, что М замкнутый класс. Рассмотрим функцию ФÎ[M], Ф = f(f1, ..., fm), где f, f1, ..., fmÎM, причем можем считать, что все они зависят от n переменных. Пусть набор  = (a1, ..., an),
= (a1, ..., an),  = (b1, ..., bn). Рассмотрим Ф(a1, ..., an) = f(f1(a1, ..., an), …, fm(a1, ..., an)) и Ф(b1, ..., bn) = f(f1(b1, ..., bn), ..., fm(b1, ..., bn)). Здесь f1(a)
= (b1, ..., bn). Рассмотрим Ф(a1, ..., an) = f(f1(a1, ..., an), …, fm(a1, ..., an)) и Ф(b1, ..., bn) = f(f1(b1, ..., bn), ..., fm(b1, ..., bn)). Здесь f1(a)  f1(b), ..., fm(a)
f1(b), ..., fm(a)
 fm(b), тогда набор (f1(a), ..., fm(a))
fm(b), тогда набор (f1(a), ..., fm(a)) (f1(b), ..., fm(b)), но тогда Ф(a)
(f1(b), ..., fm(b)), но тогда Ф(a)  Ф(b), так как fÎM, отсюда Ф = f(f1, ..., ) – монотонная функция.
Ф(b), так как fÎM, отсюда Ф = f(f1, ..., ) – монотонная функция.
Определение. Функция f есть суперпозиция над M, если f реализуется некоторой формулой над M.
Лемма о немонотонной функции. Отрицание можно получить суперпозицией констант 0 и 1, тождественной функции и немонотонной функции.
Доказательство. Пусть f(x1, ..., xn) – немонотонная функция. Тогда существуют наборы  и
и  , для которых
, для которых  но
но  Пусть i1, …, ik есть все те номера аргументов, для которых
Пусть i1, …, ik есть все те номера аргументов, для которых  , p=1, …, k. На всех остальных аргументных местах j имеем aj = bj. В выражении
, p=1, …, k. На всех остальных аргументных местах j имеем aj = bj. В выражении  заменим нули на местах i1, …, ik на x. В результате получим функцию g(x), для которой g(0) = f(
заменим нули на местах i1, …, ik на x. В результате получим функцию g(x), для которой g(0) = f( ) = 1 и g(1) = f(
) = 1 и g(1) = f( ) = 0. Функция g(x) является отрицанием.
) = 0. Функция g(x) является отрицанием.
Классы T0, T1, L, S, M пересекаются, но не совпадают, что видно из следующей таблицы, где «+» означает, что функция принадлежит данному классу и «-» – не принадлежит.
| T0 | T1 | L | S | M | |
| x | + | + | + | + | + |

| - | - | + | + | - |
| + | - | + | - | + | |
| - | + | + | - | + | |
| x1x2 | + | + | - | - | + |
A={x,  , 0, 1, x1x2) не является полной системой функций так как всегда есть функции Î Р2 не входящие в эти классы.
, 0, 1, x1x2) не является полной системой функций так как всегда есть функции Î Р2 не входящие в эти классы.
Задачи
1. Доказать, что пересечение любых двух замкнутых классов замкнуто.
2. Доказать, что объединение двух замкнутых классов не всегда замкнуто.
Теорема Поста о полноте
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T0, T1, L, S, M.
Доказательство. Докажем необходимость этого условия. Пусть система
N = {f1, f2, ...fs, ...} полна в Р2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T0, T1, L, S, M. Докажем от противного, пусть N Í Q, очевидно, [N] Í [Q] = Q, но [N] = P2, т.к. N – полна в Р2, отсюда Р2=Q, но это не так. Необходимость доказана.
Докажем достаточность. Пусть F = {f0, f1, fL, fm, fs}, где f0ÏT0, f1ÏT1, fLÏL, fsÏS и fmÏM. Покажем, что суперпозицией функций системы F можно получить полную систему G = {x1&x2,  }.
}.
1. Пусть g(x) = f0(x, …, x). Тогда g(0) = f( 0, …, 0) = 1. Далее возможны два случая:
g(1) = 1. Тогда g(x) º 1. Функция h(x) = f1(g(x), …, g(x)) = f1(1, …, 1) = 0, т.е. h(x) º 0. Получили константы 0 и 1;
g(1) = 0. Тогда g(x) = . По лемме о несамодвойственной функции суперпозицией над {fs,
. По лемме о несамодвойственной функции суперпозицией над {fs,  } можно получить одну из констант, например, 0. Тогда f0(0, …, 0) = 1 есть другая константа.
} можно получить одну из констант, например, 0. Тогда f0(0, …, 0) = 1 есть другая константа.
В обоих случаях получили обе константы.
2. По лемме о немонотонной функции суперпозицией над {fm, 0, 1} можно получить отрицание.
3. По лемме о нелинейной функции суперпозицией над {fL, 1,  } можно получить конъюнкцию. Теорема доказана.
} можно получить конъюнкцию. Теорема доказана.
Следствие. Всякий замкнутый класс функций из Р2, не совпадающий с Р2 содержится, по крайней мере, в одном из замкнутых классов T0, T1, L, S, M. Действительно, если N не является подмножеством Q, то [N] = P2, что неверно.
Примеры использования теоремы Поста.
1. Покажем, что система функций {f1 =x1x2, f2 =0, f3 =1, f4 = x1Åx2Åx3} полна в Р2. Составим таблицу, которая называется критериальной :
| Т0 | Т1 | L | M | S | |
| x1x2 | + | + | - | + | - |
| + | - | + | + | - | |
| - | + | + | + | - | |
| x1Åx2Åx3 | + | + | + | - | + |
| x1 x2 x3 | x1Åx2Åx3 |
| 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Из таблицы видно, что какой бы класс мы ни взяли, всегда есть функция из данной системы , которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус».
Отметим еще одно обстоятельство, касающееся приведенной системы. Какую бы функцию из этой системы мы ни удалили, система станет неполной, действительно, {f2, f3, f4}ÌL, {f1, f3, f4}ÌT1, {f1, f2, f4}ÌT0, {f1, f2, f3}ÌM.
Мы знаем, что система {x1|x2} – полна в Р2. Какова для нее критериальная таблица? x1|x2== x1x2Å1.
| Т0 | Т1 | L | M | S | |
| x1|x2 | - | - | - | - | - |
Составим критериальную таблицу для другой полной системы функций из Р2: {0, 1, x1x2, x1Åx2}.
4. Выясним, полна ли система . Составим критериальную таблицу, очевидно . Чтобы показать, что , достаточно найти одну функцию и . Возьмем ,… и А – полная система функций. Определение. Система функций {f1, ..., fs, ...} называется базисом в Р2,если она полна в Р2, но любая ее подсистема не…Теорема о достаточности четырех функций.
Доказательство. Пусть {f0, f1, fL, fM, fS} – полная система функций, тогда она не лежит целиком ни в одном из классов T0, T1, L, M, S.… Если f0(1, ..., 1) = 0, то f0ÏT1 и f0ÏM, тогда {f0, fS, fL} – полная… Если f0(1, ..., 1) = 1, то f0ÏS и {f0, f1, fL, fM } образует полную систему из четырех функций.Задачи и упражнения по функциям алгебры логики
1. – коммутативность связки *, где символ * является общим обозначением для связок &, Ú, Å, ~, |, ¯. 2. – ассоциативность связки *, где *– общее обозначение для связок… 3. ДистрибутивностьМИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ
Минимизация нормальных форм
Если для всякого набора = (a1, ..., an) значений переменных условие g()=1 влечёт , то функция g называется частью функции f (или функция f накрывает… Элементарная конъюнкция K называется импликантом функции f, если для всякого… Импликант K функции f называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не…Алгоритм Квайна построения сокращенной ДНФ.
2. Провести все операции неполного склеивания. 3. Провести все операции поглощения. Пример 1. Построим сокращенную ДНФ для функции, приведенной в таблице 3.1.Метод Блейка
Пример 2. Построить сокращенную ДНФ по ДНФ D функции f(x,y,z), где После первого этапа получаем: После второго этапа получаем сокращенную ДНФ:Алгоритм построения сокращенной ДНФ с помощью КНФ
Пусть f(x1, … , xn) есть некоторая функция алгебры логики. Построим для f некоторую КНФ. Осуществим далее следующие преобразования. 1. В КНФ раскроем скобки и удалим дублирующие члены, затем удалим… 2. В полученном выражении удалим нулевые дизъюнктивные слагаемые.Построение всех тупиковых ДНФ.
1. Построим СДНФ функции f, и пусть P1, P2, …,Pn есть ее коституенты единицы). 2. Построим сокращенную ДНФ функции, f и пусть K1, K2, …, Km – ее простые… 3. Построим матрицу покрытий простых импликант функции f ее конституентами единицы (табл. 3.4), полагая, чтоАлгоритм минимизации функций в классе ДНФ
1. Строим СДНФ функции f.
2. Строим сокращенную ДНФ функции f.
3. С помощью матрицы покрытий и решеточного выражения строим все ТДНФ функции f.
4. Среди построенных ТДНФ выбираем все минимальные дизъюнктивные нормальные формы функции f.
Алгоритм минимизации функций в классе КНФ
Чтобы построить все минимальные КНФ (МКНФ) функции f, следует построить все МДНФ функции `f и взять от каждой из них отрицание, для чего заменить знаки & на Ú , а Ú на & ( сохранив первоначальное распределение скобок) и над каждой буквой поставить знак отрицания. Полученные КНФ для функции f будут минимальными. В самом деле, если бы для f существовала КНФ с меньшим числом букв, то ее отрицание дало бы для `f ДНФ с меньшим числом букв, чем в любой из минимальных ДНФ для `f. Противоречие с их минимальностью.
Алгоритм минимизации функций в классе нормальных форм
Пусть f – функция алгебры логики.
1. Строим все МДНФ функции f.
2. Строим все МКНФ функции f.
3. Из построенных минимальных форм выбираем простейшие ( по числу букв).
Пример 6.В классе нормальных форм минимизировать функцию f=(01011110).
1. Строим СДНФ для функции f :

2. Строим сокращенную ДНФ функции f:

3. Строим матрицу покрытий (таблица 3.6).
Таблица 3.6
| N | ПИ | `x`y z `x y z x`y`z x`y z x y`z |
| `x z `y z x`y x`z | + + + + + + + + |
Решеточное выражение E = ( 1 Ú 2 ) 1 (3 Ú 4 ) 4 = 134 Ú 124.
4. Строим все тупиковые ДНФ функции f :


5. Обе построенные ТДНФ являются минимальными.
6. Повторяем эти этапы для функции `f.
СДНФ : 
Сокращенная ДНФ : 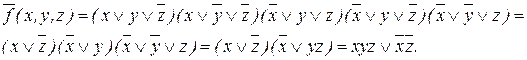
Строим матрицу покрытий (таблица 3.7).
Таблица 3.7
| N | ПИ | x`y`z `x y`z x y z |
| `x`z x y z | + + + |
Решеточный многочлен E = 112 = 12. Единственная тупиковая ДНФ (она же минимальная) для функции 
 Минимальная КНФ функции
Минимальная КНФ функции  Из построенных МДНФ и МКНФ выбираем простейшую
Из построенных МДНФ и МКНФ выбираем простейшую 
Пример 7. В классе нормальных форм минимизировать функцию f=(11011011).
1. СДНФ: 
2. Сокращенная ДНФ : 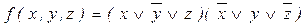 =
=
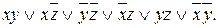
3. Строим матрицу покрытий (таблица 3.8).
Таблица 3.8
| N | ПИ | `x`y`z `x`y z `x y z x`y`z x y`z x y z |
| x y x`z y`z `x z y z `x`y | + + + + + + + + + + + + |
E = ( 3 Ú 6 ) ( 4 Ú 6 ) ( 4 Ú 5 ) ( 2 Ú 3 ) ( 1 Ú 2 ) ( 1 Ú 5 ) = 1246 Ú 1356 Ú 134 Ú 256 Ú 2345.
4. Тупиковые ДНФ функции f :




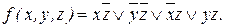
5. Минимальные ДНФ функции f :


6. Повторяем указанные выше этапы для функции `f .
СДНФ : 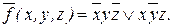
Сокращенная ДНФ :
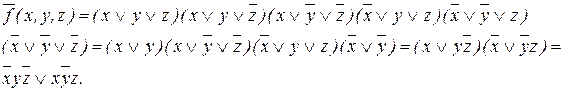
Построенная сокращенная ДНФ функции `f является для нее тупиковой и минимальной .
Минимальная КНФ функции 
Построенные МДНФ и МКНФ имеют одно и то же число букв; все они составляют минимальные формы для f :



Минимизация частично определенных функций
Задача минимизации частично определенной функции f сводится к отысканию такого доопределения g функции f, которое имеет простейшую (по числу букв )… Обозначим через f0(x1,…,xn) и f1(x1,…,xn) доопределения нулями и единицами… Теорема. Минимальная ДНФ частично определенной функции f(x1,…,xn) есть дизъюнкция самых коротких импликант в…Алгоритм минимизации частично определенных функций
В классе ДНФ
1. Строим СДНФ функции f0 .
2. Строим сокращенную ДНФ функции f1 .
3. С помощью матрицы покрытий коституент единицы функции f0 простыми импликантами функции f1 и решеточного выражения строим все тупиковые ДНФ (для некоторых доопределений функции f ) .
4. Среди полученных ТДНФ выбираем простейшие, они являются минимальными ДНФ ( для некоторых доопределений функции f ) .
Алгоритм минимизации частично определенных функций
В классе КНФ
Построение минимальных КНФ для частично определенной функции аналогично построению минимальных КНФ для всюду определенной функции.
Алгоритм минимизации частично определенных функций в классе нормальных форм аналогичен алгоритму минимизации в классе нормальных форм для всюду определенных функций.
Пример 1.В классе нормальных форм минимизировать частично определенную функцию f ( x, y, z, t ) = (1---010010-01--1)
Решение. Минимизируем функцию f в классе ДНФ.
1. Строим сокращенную ДНФ для доопределения единицами f1 функции f по таблице 3.9.
Таблица 3.9
| x y z t | f f0 f1 `f h0 h1 |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 | 1 1 1 0 0 0 - 0 1 - 0 1 - 0 1 - 0 1 - 0 1 - 0 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 - 0 1 - 0 1 0 0 0 1 1 1 1 1 1 1 1 1 - 0 1 - 0 1 - 0 1 - 0 1 1 1 1 0 0 0 |

2. Строим матрицу покрытий коституент единицы в СДНФ для доопределения нулями f0 функции f с помощью построенной сокращенной ДНФ для f1 ( таблица 3.10).
Таблица 3.10
| N | ПИ | 
| 
| 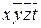
| 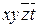
| 
|

| + | + | ||||

| + | |||||

| + | + | ||||

| + | + | ||||

| + | |||||

| + |
3. По таблице строим решеточный многочлен
E = (2Ú4)(5Ú6)(3Ú4)(1Ú3)1 = 145 Ú 125 Ú 146 Ú 1236.
4. Строим все тупиковые ДНФ :
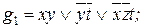

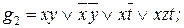

5. Из построенных тупиковых ДНФ выбираем минимальные :
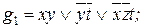

Функции g1 и g3 есть минимальные доопределения функции f в классе ДНФ.
Минимизируем теперь функцию f в классе КНФ. Для этого проведем минимизацию функции `f в классе ДНФ Пусть h0 и h1 есть доопределение нулями и единицами соответственно функции `f .
Сокращенная ДНФ для

Матрица покрытия конституент единицы в СДНФ для h0 с помощью простых импликант в сокращенной ДНФ для h1 приведена в таблице 3.11.
Таблица 3.11
| N | ПИ | 
| 
| 
| 
| 
|

| + | + | ||||

| + | + | ||||

| + | |||||

| + | |||||
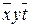
| + | + | ||||

| + |
3. Решеточное выражение E=5 (2 Ú 3 Ú5) 2 (1Ú 4)(1Ú 6) = 25(1Ú 46) = 125 Ú 2446.
4. Строим две тупиковые ДНФ:
 и
и 
Минимальная. 
5. Функция  есть минимальное доопределение функции f в классе КНФ.
есть минимальное доопределение функции f в классе КНФ.
Найденные МДНФ g1 , g3 и МКНФ  являются минимальными доопределениями функции f в классе нормальных форм.
являются минимальными доопределениями функции f в классе нормальных форм.
Техническая реализация минимальных форм для функции часто проще, а потому дешевле реализации ее СДНФ ( СКНФ ) . Следовательно, этап минимизации при конструировании логических схем является одним из важнейших.
Метод минимизирующих карт Карно
При построении сокращенных ДНФ для функций, зависящих от небольшого числа (не более 4) переменных, используется метод карт Карно. Построение карт… Множество всех двоичных наборов длины n образует n-мерный булев или двоичный… Расстоянием Хэмминга между вершинами и куба называется число оно равно числу координат, в которых наборы и отличаются…Задачи по минимизации и доопределению булевых функций
1) A = , = (00101111); 2) A = , = (01111110); 3) A = , = (1010111001011110);ЛОГИКА ВЫСКАЗЫВАНИЙ
Введение в логику высказываний
Определение. Высказыванием называется повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.
Примеры высказываний: «2х2=4», «Волга впадает в Черное море», «Москва – столица России». Первое и третье высказывания истинны, второе – ложно. Предложение «х + y = 4» не является высказыванием, т.к. оно может быть истинным при некоторых значениях х и y и ложным при других значениях. Из простых, атомарных высказываний можно сооружать сложные высказывания. Например, из двух высказываний: «Москва стоит на берегу Невы» и «Санкт-Петербург стоит на берегу Невы», из которых первое ложно, второе истинно, можно соорудить более сложные высказывания: «Москва стоит на берегу Невы или Санкт-Петербург стоит на берегу Невы» (истинное) или «Москва стоит на берегу Невы и Санкт-Петербург стоит на берегу Невы» (ложное).
В логике высказываний простые высказывания являются булевыми переменными, принимающими значения «истина» (и) или «ложь» (л). Переменной (и) соответствует 1, переменной (л) – 0. Для них стандартным образом определяются булевы функции: дизъюнкция высказываний, конъюнкция (два последних примера), отрицание, эквивалентность, сумма по mod 2 (исключающее «или»), импликация.
Рассмотрим более подробно последнюю функцию  , где P и Q – высказывания, т.е. утверждение типа: «
, где P и Q – высказывания, т.е. утверждение типа: « влечет
влечет  » или «из
» или «из  следует
следует  », например, «Если 2х2=5, то Москва – столица». Не математик найдет это выражение ложным, ибо ему кажется, что в выражении «
», например, «Если 2х2=5, то Москва – столица». Не математик найдет это выражение ложным, ибо ему кажется, что в выражении « влечет
влечет  »
»  должно по смыслу вытекать из
должно по смыслу вытекать из  , только в этом случае утверждение истинно. Но тогда получается, что логическая связка «
, только в этом случае утверждение истинно. Но тогда получается, что логическая связка «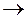 » зависит от смысла высказываний. Математики импликацию определяют стандартной таблицей истинности, которая не противоречит «здравому смыслу»: «л
» зависит от смысла высказываний. Математики импликацию определяют стандартной таблицей истинности, которая не противоречит «здравому смыслу»: «л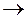 л» и «л
л» и «л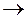 и» – эти утверждения истинны, так как из ложной посылки можно получить как ложное, так и истинное утверждение. «и
и» – эти утверждения истинны, так как из ложной посылки можно получить как ложное, так и истинное утверждение. «и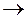 и» – истинное утверждение, так как из верной посылки с помощью верных рассуждений можно получить только истинное утверждение. «и
и» – истинное утверждение, так как из верной посылки с помощью верных рассуждений можно получить только истинное утверждение. «и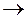 л» – ложное утверждение, ибо из истинного утверждения с помощью верных рассуждений мы не сможем прийти к ложному результату.
л» – ложное утверждение, ибо из истинного утверждения с помощью верных рассуждений мы не сможем прийти к ложному результату.
Простые высказывания (булевы переменные) будем обозначать буквами  , если понадобится, с индексами. Булевы функции от этих высказываний –
, если понадобится, с индексами. Булевы функции от этих высказываний –  . В логике высказываний можно ввести стандартное для функций алгебры логики понятие формулы. Формулы будем обозначать буквами латинского алфавита
. В логике высказываний можно ввести стандартное для функций алгебры логики понятие формулы. Формулы будем обозначать буквами латинского алфавита 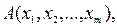 где в скобках перечислены входящие в формулу булевы переменные.
где в скобках перечислены входящие в формулу булевы переменные.
Формула 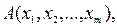 называется тавтологией, если она принимает значение 1 для любого набора значений входящих в нее переменных, т.е. если она реализует функцию константа 1.
называется тавтологией, если она принимает значение 1 для любого набора значений входящих в нее переменных, т.е. если она реализует функцию константа 1.
Формула 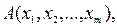 называется противоречием, если она принимает значение 0 на всех наборах значений переменных
называется противоречием, если она принимает значение 0 на всех наборах значений переменных  (реализует функцию константа 0).
(реализует функцию константа 0).
Формула 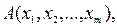 называется опровержимой, если существует набор
называется опровержимой, если существует набор  значений
значений  , такой что
, такой что 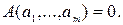
Формула 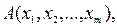 называется выполнимой, если существует набор
называется выполнимой, если существует набор  значений
значений  , такой что
, такой что 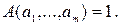
С точки зрения логики тавтология – логический закон, так как при любой подстановке вместо переменных конкретных высказываний мы получаем истинное высказывание. Перечислим наиболее важные тавтологии (А, В, С – произвольные формулы):
1.  т.е.
т.е.  Эта тавтология называется законом исключенного третьего или tertium nondatur.
Эта тавтология называется законом исключенного третьего или tertium nondatur.
2. 
3.  – цепное рассуждение.
– цепное рассуждение.
4. 
5. 
6. 
7. 
8.  – закон Пирса.
– закон Пирса.
Любую из этих тавтологий можно обосновать, составив таблицу истинности и показав, что соответствующая функция есть константа. К этому же результату можно прийти с помощью эквивалентных преобразований.
Докажем, что  – тавтология.
– тавтология.

При доказательстве различных утверждений мы пользуемся «рассуждениями».
Рассуждение называется правильным, если из конъюнкции посылок  следует заключение D, это записывается:
следует заключение D, это записывается:  , т.е. всякий раз, когда все посылки истинны, то заключение тоже истинно. Таким образом, чтобы установить правильность рассуждений, надо показать, что формула
, т.е. всякий раз, когда все посылки истинны, то заключение тоже истинно. Таким образом, чтобы установить правильность рассуждений, надо показать, что формула  является тавтологией. Действительно, если какая-то из посылок ложна, то
является тавтологией. Действительно, если какая-то из посылок ложна, то  и импликация принимает значение 1. Если все посылки истинны и рассуждения верны, то заключение тоже должно быть верно и импликация вновь принимает значение 1.
и импликация принимает значение 1. Если все посылки истинны и рассуждения верны, то заключение тоже должно быть верно и импликация вновь принимает значение 1.
Пример 1. Рассмотрим следующее «рассуждение»: «Если число 5 – простое, то оно нечетное. Число 5 – нечетное, следовательно, оно простое». Число 5 действительно простое, но сами рассуждения неверны. Введем обозначения для высказываний: х – «5 – число простое», y – «5 – число нечетное». Тогда посылками будут  заключением будет х. Рассуждения шли по схеме
заключением будет х. Рассуждения шли по схеме  Строим формулу для определения правильности рассуждения:
Строим формулу для определения правильности рассуждения:  Проверим,
Проверим,

На наборе х = 0, y = 1 формула принимает значение 0, следовательно, она не является тавтологией. Эта формула будет тавтологией, если х = y, т.е. простое число и нечетное число – эквивалентные понятия. «Здравый смысл подсказывает», что в этом случае, действительно, рассуждения верны.
Пример 2. Если Петр занимается спортом, то Петр никогда не болеет. Петр занимается спортом, следовательно, он не болеет.
Введем обозначения для высказываний: x – «Петр занимается спортом», y – «Петр не болеет».
Схема рассуждений  Проверим правильность этой схемы рассуждений:
Проверим правильность этой схемы рассуждений: 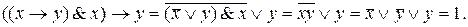
Распространенные схемы правильных рассуждений: 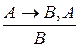 и
и 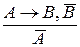 . Правильность первой схемы доказана в примере 2. Докажем правильность второй схемы:
. Правильность первой схемы доказана в примере 2. Докажем правильность второй схемы:
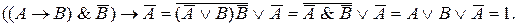
Рассмотрим высказывание вида 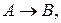 где А – конъюнкция посылок, В – заключение. Если формула А – тавтология и рассуждения логически правильны, то заключение В принимает значение «истина», что следует из таблицы истинности для импликации. Такие методы доказательства истинности заключения называются прямыми. Иногда удобнее доказать истинность другого высказывания, эквивалентного данному. Такие формы доказательства называются косвенными. Одним из них является метод доказательства от противного.
где А – конъюнкция посылок, В – заключение. Если формула А – тавтология и рассуждения логически правильны, то заключение В принимает значение «истина», что следует из таблицы истинности для импликации. Такие методы доказательства истинности заключения называются прямыми. Иногда удобнее доказать истинность другого высказывания, эквивалентного данному. Такие формы доказательства называются косвенными. Одним из них является метод доказательства от противного.
1. Предполагаем, что высказывание  ложно и приходим к противоречию, получаем, что истинными являются два высказывания:
ложно и приходим к противоречию, получаем, что истинными являются два высказывания:  и
и  , т.е.
, т.е.  Применимость этой формы доказательства оправдывается следующей эквивалентностью:
Применимость этой формы доказательства оправдывается следующей эквивалентностью: 
2. Существуют и другие схемы доказательства от противного. Предполагаем, что из  следует
следует  и приходим к тому, что истинными оказываются
и приходим к тому, что истинными оказываются  и
и  или
или  и
и  . Эти схемы основаны на эквивалентности
. Эти схемы основаны на эквивалентности  или
или  .
.
Действительно,  и
и 
Другой метод косвенного доказательства – доказательство по закону контрапозиции, когда вместо истинности 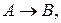 мы доказываем истинность
мы доказываем истинность  . Действительно,
. Действительно, 
Рассмотрим на конкретных задачах применение исчисления высказываний.
Пример 3. Записать составное высказывание в виде формулы, употребляя булевы переменные для обозначения простых высказываний.
а) если идет дождь, то дует ветер и становится холодно;
б) если дует ветер, идет дождь;
в) ветер дует тогда и только тогда, когда идет дождь;
г) неверно, что ветер дует тогда и только тогда, когда нет дождя.
Решение.Введем обозначения: х – «идет дождь», у – «дует ветер», z –«становится холодно».
Тогда приведенные высказывания можно записать в виде следующих формул: а)  б)
б)  в)
в)  г)
г)  .
.
Пример 4. Выяснить, являются ли следующие рассуждения логически верными.
Если Джонс не встречал ночью Смита, то Смит был убийцей или Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство имело место после полуночи, то Смит был убийцей или Джонс не лжет. Следовательно, Смит был убийцей.
Решение. Введем логические переменные: х – «Джонс не встречал ночью Смита», у – «Смит убийца», z – «Джонс лжет», t – «убийство состоялось после полуночи». Прежде чем записать формулу, надо уточнить по условию задачи в каком контексте употребляется союз «или». Когда мы говорим «А или В», мы можем подразумевать две разные ситуации: а)  или б)
или б)  Во втором случае высказывания А и В не могут быть одновременно истинными. Чтобы подчеркнуть этот момент, обычно говорят «либо А, либо В». В нашей задаче нет такой оговорки, поэтому мы можем для записи высказывания: «Смит был убийцей или Джонс не лжет» использовать формулу
Во втором случае высказывания А и В не могут быть одновременно истинными. Чтобы подчеркнуть этот момент, обычно говорят «либо А, либо В». В нашей задаче нет такой оговорки, поэтому мы можем для записи высказывания: «Смит был убийцей или Джонс не лжет» использовать формулу  . Итак, мы имеем посылки:
. Итак, мы имеем посылки:  ,
,  ,
,  заключение: у. Надо составить формулу:
заключение: у. Надо составить формулу:
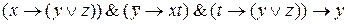 и посмотреть, будет ли она тавтологией:
и посмотреть, будет ли она тавтологией:

Следовательно, рассуждения логически правильны.
Пример 5. Проверить совместность утверждений.
Либо свидетель не был запуган, либо, если Генри покончил жизнь самоубийством, то записка была найдена. Если свидетель был запуган, то Генри не покончил жизнь самоубийством. Если записка была найдена, то Генри покончил жизнь самоубийством.
Решение. Введем булевы переменные: х – «свидетель не запуган», у – «Генри покончил самоубийством», z – «записка найдена». Составим конъюнкцию посылок и посмотрим, не является ли она противоречием.
Здесь употреблено выражение «либо..., либо...», поэтому первое составное высказывание следует записать в виде  что эквивалентно
что эквивалентно  Конъюнкция посылок имеет вид:
Конъюнкция посылок имеет вид:
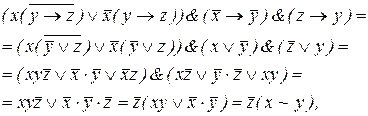
это не равно тождественному 0, следовательно, высказывания не являются противоречивыми.
Пример 6. Четыре ученицы: Маша (М), Нина (Н), Ольга (О) и Поля (П) участвовали в соревнованиях и заняли первые 4 места. На вопрос, кто какое место занял, было дано 3 ответа:
1) О – второе, П – третье;
2) О – первое, Н – второе;
3) М – второе, П – четвертое.
В каждом из этих ответов одна часть верна, а другая нет. Какое место заняла каждая девушка?
Решение. Введем булевы переменные: х – «О – второе», у – «П – третье», z – «О – первое», t – «Н – второе», u – «М – второе», n – «П – четвертое». Получим систему уравнений:  так как если x истинно, тогда y ложно, а
так как если x истинно, тогда y ложно, а  – истинно и
– истинно и  либо
либо  Аналогично,
Аналогично,  Удобнее записать эту систему следующим образом:
Удобнее записать эту систему следующим образом: 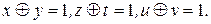
Отсюда  или
или  окончательно,
окончательно, 
Кроме того,  так как одна ученица не может занять 2 места и одно место не может быть занято двумя ученицами. В результате в последнем уравнении останется единственный ненулевой член
так как одна ученица не может занять 2 места и одно место не может быть занято двумя ученицами. В результате в последнем уравнении останется единственный ненулевой член  Отсюда
Отсюда  или О – первая, М – вторая, П – третья, Н – четвертая.
или О – первая, М – вторая, П – третья, Н – четвертая.
Пример 7.Во время перемены в классе были Аня, Борис, Ваня и Майя. Один из них разбил окно. На вопрос:”Кто разбил окно?”, были даны ответы:
Аня: 1) Я не разбивала. 2) Я сидела и читала. 3) Майя знает, кто разбил.
Борис: 1) Я этого не делал. 2) С Майей я давно не разговариваю. 3) Это сделал Ваня.
Ваня: 1) Я не виновен. 2) Разбила Майя. 3) Борис лжёт, говоря, что разбил я.
Майя: 1) Я не разбивала. 2) Это вина Ани. 3) Борис знает, что я не виновна, т.е. мы с ним беседовали во время перемены.
Затем каждый признался, что из трёх ответов каждого, два – истинны, а один ложный. Кто разбил окно?
Решение. Введем булевы переменные. Высказывания, принадлежащие Ане, обозначим буквами  с индексами
с индексами  ; высказывания, принадлежащие Борису –
; высказывания, принадлежащие Борису –  соответственно, принадлежащие Ване –
соответственно, принадлежащие Ване –  и принадлежащие Майе –
и принадлежащие Майе –  .
.
Запишем все формулы, которые являются тавтологиями, получим уравнения:
 ;
;
 ;
;
 ;
;
 .
.
Выпишем все противоречия:





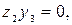




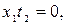

Чтобы иметь возможность воспользоваться этими противоречиями, возьмём конъюнкцию двух тавтологий:
 и
и 
что тоже будет тавтологией. Получим 

В этой формуле слева останется всего три ненулевых члена:
 или
или 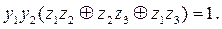 Последнее уравнение даёт
Последнее уравнение даёт 
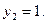 Так как
Так как  и
и  то
то 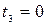 и следовательно,
и следовательно,  а
а  Следовательно, окно разбила Аня.
Следовательно, окно разбила Аня.
Рассмотрим еще одну задачу, для решения которой не требуется аппарат логики высказываний, но тем не менее эта задача относится к логическим задачам.
Пример 8. В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас имеет белые, один черные, а один рыжие волосы, но ни у кого цвет волос не совпадает с фамилией», – заметил черноволосый. «Ты прав», – сказал Белов. Какой цвет волос у художника?
Решение.Составим таблицу.
| Фамилия Цвет волос | Б | Ч | Р |
| б | |||
| ч | |||
| р |
|

| Фамилия Цвет волос | Б | Ч | Р |
| б | |||
| ч | |||
| р |
Из условия задачи ясно, что черноволосый не Белов, поэтому первый вариант не подходит. Следовательно, Белов – рыжий, Чернов – белый, Рыжов – черный.
Пример 9. На склад, имеющий два помещения для хранения больших количеств двух видов топлива – угля и кокса, каждого отдельно, поступают грузовики, каждый всякий раз с одним из этих видов топлива. К механизму, открывающему шахты, предъявляется требование, чтобы он открыл шахту в помещении для угля, если прибывает грузовик с этим топливом, и шахту в помещении для кокса, если прибывает грузовик с коксом. Для обеспечения хорошей сортировки топлива было предъявлено дополнительное требование: всякий раз в помещение склада впускается только один грузовик и открывается лишь одна шахта.
Спрашивается, имеет ли этот механизм также следующее свойство: если не въехал в помещение склада грузовик с углем, то шахта для угля не откроется, а если не въехал грузовик с коксом, то не откроется шахта для кокса.
Решение. Введем булевы переменные: высказывание « прибыл грузовик с углем» обозначим через x, « прибыл грузовик с коксом» – y, «открыта шахта для угля» – z, «открыта шахта для кокса» – t. Тогда посылками будут: 
 заключение
заключение  Задача сводится к тому, чтобы выяснить, правильны ли рассуждения
Задача сводится к тому, чтобы выяснить, правильны ли рассуждения 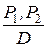 , т. е. вытекает ли это заключение из конъюнкции посылок. Кроме того, имеются два дополнительных условия, что может въехать только одна машина и открывается лишь одна дверь. Эти условия можно задать равенствами:
, т. е. вытекает ли это заключение из конъюнкции посылок. Кроме того, имеются два дополнительных условия, что может въехать только одна машина и открывается лишь одна дверь. Эти условия можно задать равенствами: 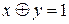 и
и  .
. 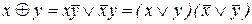 аналогично,
аналогично,  (представление в виде СДНФ или СКНФ). Построим формулу:
(представление в виде СДНФ или СКНФ). Построим формулу: 
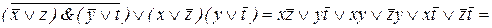
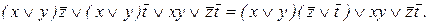
Так как 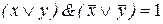 , то
, то  аналогично,
аналогично,  , следовательно,
, следовательно, 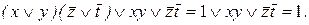 Мы получили тавтологию, следовательно, рассуждения верны.
Мы получили тавтологию, следовательно, рассуждения верны.
Пример 10. На предприятии есть три цеха: A, B, C, договорившиеся о порядке утверждения проектов, а именно:
1. Если цех B не участвует в утверждении проекта, то в этом утверждении не участвует и цех A.
2. Если цех B принимает участие в утверждении проекта, то в нем принимают участие цеха A и C.
Спрашивается, обязан ли при этих условиях цех C принимать участие в утверждении проекта, когда в нем принимает участие цех A?
Решение. Логические переменные: « А участвует в утверждении проекта» обозначим через А, «В участвует в утверждении проекта» – В, «С участвует в утверждении проекта» – С. Посылки: 
 . Утверждение
. Утверждение  Надо выяснить, верны ли рассуждения, т.е. выяснить будет ли тавтологией формула:
Надо выяснить, верны ли рассуждения, т.е. выяснить будет ли тавтологией формула: 

 следовательно, рассуждения верны.
следовательно, рассуждения верны.
Пример 11. Перед судом стоят три человека, из которых каждый может быть либо туземцем, либо колониалистом. Судья знает, что туземцы всегда отвечают на вопросы правдиво, между тем как колониалисты всегда лгут. Однако судья не знает, кто из них туземец, а кто колониалист. Он спрашивает первого, но не понимает его ответа. Поэтому он спрашивает сначала второго, а потом третьего о том, что ответил первый. Второй говорит, что первый назвал себя туземцем. Третий говорит, что первый назвал себя колониалистом. Кем были второй и третий подсудимые?
Решение. Во-первых, если первый человек туземец, то он назовет себя туземцем, если он колониалист, то тоже назовет себя туземцем. Высказывание «первый сказал, что он туземец» обозначим через x, «второй туземец» – y, «третий туземец» – z, и заметим, что x º 1.
Имеем 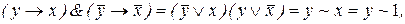 следовательно, второй – туземец.
следовательно, второй – туземец.  следовательно, третий – колониалист.
следовательно, третий – колониалист.
Задачи по алгебре высказываний
a) Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива. b) Или Сэм пойдет на вечеринку, и Макс не пойдет на нее; или Сэм не пойдет на… c) Необходимое и достаточное условие счастья для шейха состоит в том, чтобы иметь вино, женщин и услаждать свой слух…Список литературы
1. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1986. –384 с.
2. Нефедов В.Н., Осипова В.А. Курс дискретной математики – М.: Издательство МАИ, 1992. –264с.
3. Мендельсон Э. Введение в математическую логику. – М.: Наука, 1984. –319с.
4. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.: Наука, 1992. –408с.
5. Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач на алгебре и теории чисел. – М. : Просвещение, 1993.
6. Набебин А.А. Логика и пролог в дискретной математике. – М.: МЭИ, 1996. –452с.
7. Кольман Э. Зих О. Занимательная логика. – М.: Наука, 1966. –127с.
8. Сборник конкурсных задач по математике для поступающих во втузы./Под ред. Сканави М.И. – М.: Высшая школа, 1980. –541с.
9. Рембольд У. Введение в информатику для научных работников и инженеров. – Уфа: УГАТУ, 1996. –445с.
– Конец работы –
Используемые теги: УСМАНОВА, Зинира, Масгутовна0.057
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: УСМАНОВА Зинира Масгутовна
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов