Алгоритм умножения

Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в особую таблицу, называемую таблицей умножения однозначных чисел, и запоминают.

Естественно, что смысл умножения сохраняется и для многозначных чисел, но меняется техника вычислений. Произведение многозначных чисел, как правило, находят, выполняя умножение столбиком, по определенному алгоритму. Выясним, каким образом возника­ет этот алгоритм, какие теоретические факты лежат в его основе.

Умножим, например, столбиком 428 на 263.

´ 263

+ 2568

856__

Видим, что для получения ответа нам пришлось умножить 428 на 3, 6 и 2, т.е. умножить многозначное число на однозначное; но, умножив на 6, результат записали по - особому, поместив единицы числа 2568 под десятками числа 1284, так как умножали на 60 и получили число 25680, но нуль в конце записи опустили. Слагаемое 856 - это результат умножения на 2 сотни, т.е. число 85600. Кроме того, нам пришлось найти сумму многозначных чисел.

Итак, чтобы выполнять умножение многозначного числа на многозначное, необходимо уметь:

- умножать многозначное число на однозначное и на степень десяти;

- складывать многозначные числа.

Сначала рассмотрим умножение многозначного числа на однозначное.

Умножим, например, 428 на 3. Согласно правилу записи чи­сел в десятичной системе счисления, 428 можно представить в виде 4 ×10² + 2 ×10 + 8 и тогда 428×3 = (4×10² + 2 ×10+ 8)×3. На основании дистрибутивности умножения относительно сложения раскроем скобки: (4 × 10²+ (2×10)×3 + 8 ×3. Произведения в скобках могут быть найде­ны по таблице умножения однозначных чисел: 12×10² + 6 ×10 + 24. Видим, что умножение многозначного числа на однозначное свелось к умножению однозначных чисел. Но чтобы получить окончательный результат, надо преобразовать выражение 12×10² + 6 ×10 + 24 - коэф­фициенты перед степенями 10 должны быть меньше 10. Для этого представим число 12 в виде 1 ·10 + 2, а число 24 в виде 2·10 + 4. Затем в выражении (1·10 + 2) ·10² + 6·10 + (2·10 + 4) раскроем скобки: 1·10³+2·10²+6·10+2·10+4. На основании ассоциативности сложения и дистрибутивности умножения относительно сложения сгруппируем слагаемые 6·10 и 2·10 и вынесем 10 за скобки: 1·10³ + 2·10² + (6 + 2) ·10+4. Сумма 6+2 есть сумма однозначных чисел и может быть найдена по таблице сложения: 1 · 10³ + 2·10² + 8 ·10 + 4. Полученное выражение есть десятичная запись числа 1284, т. е. 428·3 = 1284.

Таким образом, умножение многозначного числа на однозначное основывается на:

- записи чисел в десятичной системе счисления;

- свойствах сложения и умножения;

- таблицах сложения и умножения однозначных чисел.

Выведем правило умножения многозначного числа на однозначное в общем виде.

Пусть требуется умножить х = а_n × 10 ⁿ + а _{n – 1} × 10 ^{n – 1} + …+ а₁ × 10 + а₀ на однозначное число у:

х × у = (а_n × 10ⁿ + а_{n – 1} × 10^{n – 1} + …+ а₁ × 10 + а₀) × у = (а_n × у) × 10ⁿ +( а_{n – 1} × у) × 10^{n – 1} + … + а₀ × у причем преобразования выполнены на основании свойств умножения. После этого, используя таблицу умножения, заменяем все произведения а_k × у, где 0 £ k £ n, соответствующими значениями а_k × у = b _k ×10 + с и получаем: х× у = (b_п×10 + с_п ) + (b_{п - 1}×10+ с_{п - 1} ) ×10^{п - 1} + ... +(b₁×10 + с₁ ) ×10 + (b₀×10 + с₀) = b_п ×10^{п + 1} + (с_п + b_{п - 1}) ×10 ^п + ... + (с₁ + b₀) ×10 + с₀. По таблице сложения заменяем суммы с_k + b_{k - 1}, где 0 £ k £ n и k = 0, 1, 2, ..., n, их значениями. Если, например, с₀ однозначно, то последняя цифра произведения равна с₀ . Если же с₀ = 10 + m₀, то последняя цифра равна m₀ , а к скобке (с₁ + b₀) надо прибавить 1. Продолжая этот процесс, получим десятичную запись числа х × у.

Описанный процесс позволяет сформулировать в общем видеалгоритм умножения многозначного числа на однозначное число у.

1. Записываем второе число под первым.

2. Умножаем цифры разряда единиц числа х на число у. Еслипроизведение меньше 10, его записываем в разряд единиц ответа и переходим к следующему разряду (десятков).

3. Если произведение цифр единиц числа х на число у большеили равно 10, то представляем его в виде 10q₁ + с₀, где с₀ – однозначное число; записываем с₀ в разряд единиц ответа и запоминаем q₁ - перенос в следующий разряд.

4. Умножаем цифры разряда десятков на число у, прибавляемк полученному произведению число q₁ и повторяем процесс, описанный пп. 2 и 3.

5. Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда.

Как известно, умножение числа х на число вида 10^k сводится к приписыванию к десятичной записи данного числа k нулей. Покажем это. Умножим число х = а_n × 10ⁿ + а_{n – 1} × 10^{n – 1} + …+ а₁ × 10 + а₀ на 10^k : (а_n × 10ⁿ + а_{n – 1} × 10^{n – 1} + …+ а₁ × 10 + а₀) × 10 ^k = а_n × 10^{n+ k} + а_{n – 1} × 10^{n+ k – 1} + …+ а₀ × 10^k . Полученное выражение является суммой разрядных слагаемых числа 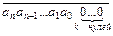, так как равно a_n × 10^{n+ k} + а_{n – 1} × 10^{n+ k – 1} + …+ а₀ × 10^k + 0 ×10^k-1 + 0× 10^k–2+ …+ 0× 10 + 0.

Например,

347·10³=(3·10²+4·10+7)·10³=3·10⁵+4·10⁴+7·10³=3·10⁵+4·10⁴+7·10³+0·10²+0·10+0= =347000

Заметим еще, что умножение на число у× 10 ^k , где у – однозначное число сводится к умножению на однозначное число у и на число 10 ^k . Например, 52×300 = 52×(3×10²) = (52×3) ×10² = 156×10² = 15600.

Рассмотрим теперь алгоритм умножения многозначного числа на многозначное. Обратимся сначала к примеру, с которого начинали, т.е. к произведению 428×263. Представим число 263 в виде суммы 2×10² + 6×10 + 3 и запишем произведение 428×(2×10² + 6×10 + 3). Оно, согласно дистрибутивности умножения относительно сложения, равно 428×(2×10²) + 428×(6×10) + 428×3. Отсюда, применив ассоциативное свойство умножения, получим: (428×2) ×10² + (428×6) ×10 + 428×3. Видим, что умножение многозначного числа 428 на многозначное число 263 свелось к умножению многозначного числа 428 на однозначные числа 2,6 и 3, а также на степени 10.

Рассмотрим умножение многозначного числа на многозначное в общем виде.

Пусть х и у - многозначные числа, причем у = b_m × 10^m + b_{m – 1} × 10^{m – 1} + …+ b₀. В силу дистрибутивности умножения относитель­но сложения, а также ассоциативности умножения можно записать:

х× у = х× (b_m × 10^m + b_{m – 1} × 10^{m – 1} + …+ b₀) = (х× b_m) × 10 ^m + (х× b_{m – 1} )× 10^{m – 1} + …+ b₀× х. Последовательно умножая число х на однозначные числа b_m, b_{m – 1}, …, b₀, а затем на 10 ^m, 10 ^{m – 1}, …, 1, получаем слагаемые, сумма которых равна х× у.

Сформулирует в общем виде алгоритм умножения числа х = на число у = .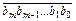

1. Записываем множитель х под ним второй множитель у.

2. Умножаем число х на младший разряд b₀ числа у и записываем произведение х × b₀ под числом у.

3. Умножаем число х на следующий разряд b₁ числа у и записываем произведение х × b₁, но со сдвигом на один разряд влево, что соответствует умножению х × b₁ на 10.

4. Продолжаем вычисление произведений до вычисления х × b_k.

5. Полученные k + 1 произведения складываем.

Изучение алгоритма умножения многозначных чисел в начальном курсе математики, как правило, проходит в соответствии с выделенными этапами. Различия имеются только в записи. Например, при обосно­вании случая умножения многозначного числа на однозначное пишут:

428 × 3 = (400 + 20 + 8) × 3 == 400× 3 + 20× 3 + 8× 3 == 1200 + 60 + 24 = 1284.

Основой выполненных преобразований являются:

- представление первого множителя в виде суммы разрядных слагаемых (т.е. запись числа в десятичной системе счисления);

- правило умножения суммы на число (или дистрибутивность умножения относительно сложения);

- умножение «круглых» (т.е. оканчивающихся нулями) чиселна однозначное число, что сводится к умножению однозначных чисел.