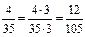Понятие дроби
 Пусть требуется измерить длину отрезка х с помощью единичного отрезка е (рис. 1). При измерении оказалось, что отрезок х состоит из трех отрезков, равных е, и отрезка, который короче отрезка е. В этом случае длина отрезка х не может быть выражена натуральным числом. Однако если отрезок е разбить на 4 равные части, то отрезок х окажется состоящим из 14 отрезков, равных четвертой части отрезка е.
Пусть требуется измерить длину отрезка х с помощью единичного отрезка е (рис. 1). При измерении оказалось, что отрезок х состоит из трех отрезков, равных е, и отрезка, который короче отрезка е. В этом случае длина отрезка х не может быть выражена натуральным числом. Однако если отрезок е разбить на 4 равные части, то отрезок х окажется состоящим из 14 отрезков, равных четвертой части отрезка е.
И тогда, говоря о длине отрезка х, мы должны указать два числа 4 и 14: четвертая часть отрезка е укладывается в отрезке точно 14 раз. Поэтому условились длину отрезка х записывать в виде 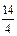 Е где Е- длина единичного отрезка е, а символ
Е где Е- длина единичного отрезка е, а символ 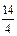 называть дробью.
называть дробью.
Определение. Пусть даны отрезок х и единичный отрезок е, длина которого Е. Если отрезок х состоит из т отрезков, равных п-ой части отрезка е, то длина отрезка х может быть представлена в виде 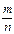 Е, где символ — называют дробью (и читают «эм энных»).
Е, где символ — называют дробью (и читают «эм энных»).
В записи дроби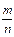 числа m и n - натуральные, m называется числителем, n - знаменателем дроби.
числа m и n - натуральные, m называется числителем, n - знаменателем дроби.
Дробь 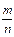 называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателяилиравен ему.
называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателяилиравен ему.
Вернемся к рисунку 1, где показано, что четвертая часть отрезка е уложилась в отрезке х точно 14 раз. Очевидно, это не единственный вариант выбора такой части отрезка е, которая укладывается в отрезке х целое число раз. Можно взять восьмую часть отрезка е, тогда отрезок х будет состоять из 28 таких частей и его длина будет выражаться дробью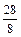 . Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью
. Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью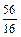
Вообще длина одного и того же отрезка х при заданном единичном отрезке е может выражаться различными дробями, причем, если длина выражена дробью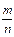 , то она может быть выражена и любой дробью вида
, то она может быть выражена и любой дробью вида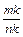 , где k- - натуральное число.
, где k- - натуральное число.
Теорема. Для того чтобы дроби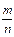 и
и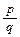 выражали длину одного того же отрезка, необходимо и достаточно, чтобы выполнялось равенство тq = пр.
выражали длину одного того же отрезка, необходимо и достаточно, чтобы выполнялось равенство тq = пр.
Доказательство этой теоремымы опускаем.
Определение.Две дроби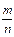 и
и 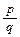 и называются равными, если тq = пр.
и называются равными, если тq = пр.
Если дроби равны, то пишут 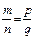
Например,  , таккак 17×21 = 119×3, а
, таккак 17×21 = 119×3, а 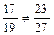 потому что 17×27 = 459, 19×23 = 437 и 459 ¹ 437.
потому что 17×27 = 459, 19×23 = 437 и 459 ¹ 437.
Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка.
Нам известно, что отношение равенства дробей рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности. Теперь, используя определение равных дробей, это можно доказать.
Теорема.Равенство дробей является отношением эквивалентности.
Доказательство. Действительно, равенство дробей рефлексивно: 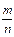 =
=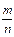 ,так как равенство mn = nm справедливо для любых натуральных чисел n и m.
,так как равенство mn = nm справедливо для любых натуральных чисел n и m.
Равенство дробей симметрично: если  , то
, то  , так как из mq = nр следует, что рn = qm (m, n, р, qÎN ). Оно транзитивно: если
, так как из mq = nр следует, что рn = qm (m, n, р, qÎN ). Оно транзитивно: если и
и 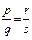 , то
, то 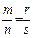 .В самом деле, так как
.В самом деле, так как 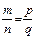 ,то тq = пр, а так как
,то тq = пр, а так как 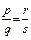 , то рs = qr. Умножив обе части равенства mq = nр на s, а равенства рs = qr на n, получим mqs = nрs и nрs = qrs. Откуда mqs =qrn или ms = nr. Последнее равенство означает, что
, то рs = qr. Умножив обе части равенства mq = nр на s, а равенства рs = qr на n, получим mqs = nрs и nрs = qrs. Откуда mqs =qrn или ms = nr. Последнее равенство означает, что 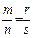 . Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
. Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
Из определения равных дробей вытекает основное свойство дроби. Напомним его.
Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.
Сокращение дробей - это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.
Если числитель и знаменатель дроби одновременно делятся только на единицу,то дробь называют несократимой.
Например, 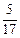 - несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу.
- несократимая дробь, так как ее числитель и знаменатель делятся одновременно только на единицу.
Приведение дробей к общему знаменателю - это замена данных дробей равными им дробями, имеющими одинаковые знаменатели.
Общим знаменателем двух дробей 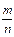 и
и  является общее кратное чисел n и q, а наименьшим общим знаменателем - их наименьшее кратное К(n, q).
является общее кратное чисел n и q, а наименьшим общим знаменателем - их наименьшее кратное К(n, q).
Например. Привести к наименьшему общему знаменателю дроби 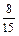 и
и 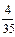 .
.
Решение. Разложим числа 15 и 35 на простые множители: 15 = 3 × 5, 35 = 5×7. Тогда К(15,35) =3× 5× 7 =105. Поскольку 105 = 15× 7 = 35 ×3, то 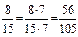 ,
,