П. 9. Сглаживание экспериментальных зависимостей. Метод наименьших квадратов

При обработке опытных данных часто приходится решать задачу, в которой необходимо исследовать зависимость одной физической величины у от другой физической величины х. Например, исследование величины погрешности размера изделия от температуры, величины износа резца от времени и т.д.

Пусть в результате опыта был получен ряд экспериментальных точек (х₁, у₁), (х₂, у₂),…, (х_n, у_n). Если построить примерный график зависимости переменной величины у от независимой переменной х, то ясно, что он не будет проходить через все полученные точки, но, по возможности, рядом с ними. По возможности, потому что производимые в ходе опыта измерения связаны с ошибками случайного характера, то и экспериментальные точки на графике обычно имеют некоторый разброс относительно общей закономерности. В силу случайности ошибок измерения этот разброс или уклонения точек от общей закономерности также являются случайными.

Задача сглаживания экспериментальной зависимости состоит в такой обработке экспериментальных данных, при которой по возможности точно была бы отражена тенденция зависимости у от х и возможно полнее исключено влияние случайных, незакономерных уклонений (1 и 2), связанных с погрешностями опыта.

Если вид зависимости у = f(x) до опыта известен из физических соображений, и на основании опытных данных требуется только определить некоторые ее параметры, чтобы зависимость сгладить, то обычно применяют «метод наименьших квадратов».

 

Итак, метод наименьших квадратов применяется для решения задач, связанных с обработкой результатов опыта, особенно важным его приложением является решение задачи сглаживания экспериментальной зависимости, т.е. изображения опытной функциональной зависимости аналитической формулой. При этом метод не решает вопроса о выборе общего вида аналитической функции, а дает возможность при заданном типе функции у = f(x)подобрать наиболее вероятные значения для параметров этой функции.

Сущность метода.

Пусть в результате опыта получены точки (х₁, у₁), (х₂, у₂),…, (х_n, у_n). Зависимость у от x , изображаемая аналитической функцией у = f(x) не может совпадать с экспериментальными значениями у_i во всех n точках, т.е разность 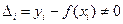. Требуется подобрать параметры функции у = f(x) таким образом, чтобы сумма квадратов этих разностей

(17)

была наименьшей. Таким образом, при методе наименьших квадратов приближение аналитической функции у = f(x) к экспериментальной зависимости считается наилучшим, если выполняется условие минимума суммы квадратов отклонений искомой аналитической функции от экспериментальной зависимости.

Рассмотрим два случая: 1) когда для изображения экспериментальной зависимости выбирается прямая, 2) когда для изображения экспериментальной зависимости выбирается парабола.

 

1) Рассмотрим случай, когда , следовательно, связь между Х и У близка к линейной, то есть рассматриваем функцию , которая наилучшим образом выражала бы зависимость у от х. Найдем коэффициенты а и b. Для этого существует метод наименьших квадратов. Пусть над системой (х, у) произведено n независимых опытов, в результате которых имеем (х₁, у₁), (х₂, у₂),…, (х_n, у_n). Требуется найти а и b такие, чтобы сумма квадратов отклонений экспериментальных точек от прямой была наименьшей, то есть, чтобы (по 16 формуле)

была наименьшей.

Из геометрических соображений ясно, что минимум z существует и реализуется в критических точках: дифференцируем эту функцию z по неизвестным параметрам a, b и приравнивая производные к нулю, получим систему двух линейных уравнений с двумя неизвестными a, b:

Преобразуем:

.

Разделим оба уравнения на n, заменим суммы по определению и получим:

, отсюда

, .

Таким образом, искомая линейная зависимость у от х имеет вид и называется выборочным (эмпирическим) уравнением регрессии у на х.

 

2) Рассмотрим случай, когда для изображения экспериментальной зависимости выбирается парабола у = аx² + bх + с. Тогда . Дифференцируя эту функцию по неизвестным параметрам a, b, c и приравнивая производные к нулю, получим систему трех линейных уравнений с тремя неизвестными a, b, c:

 

Решая систему с помощью методов Крамера или Гаусса, получим значение неизвестных параметров a, b, c, а значит, уравнение параболы.