Теорема доказана.

Так же площадь трапеции можно найти с помощью следующих формул:

1. S = mh, где m — средняя линия, h — высота трапеции.

2. Если трапеция равнобедренная, то S = 4r² / sinα, где r — радиус вписанной окружности, α — угол при основании.

3. ,
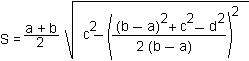где a, b — основания, c и d — боковые стороны трапеции.

 

Билет№11.

1. Основным тригонометрическим тождеством в русскоязычных учебниках математики называют соотношение 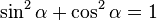, выполняющееся для произвольного значения .

Основное тригонометрическое тождество представляет собой запись теоремыПифагора для треугольника в тригонометрическом круге; длины катетов этого треугольника по модулю равны соответствующим синусу и косинусу, а гипотенуза, будучи радиусом тригонометрического круга, равна единице.

 

Пример:

 

 

Билет№8.

1) Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам.

 

2) Площадь треугольника

Одну из сторон треугольника назовем основанием треугольника. Если основание выбрано, то высотой называем высоту треугольника, проведенную к основанию.

Теорема. Площадь треугольника равна половине произведения его основания на высоту.

Даны: треугольник АВС, основание АВ=a, высота CH=h.

Доказать: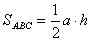

.

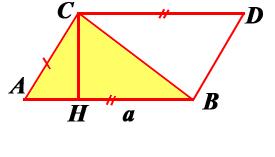Доказательство: Через вершины В и С проведем прямые, параллельные сторонам АС и АВ. Получим параллелограмм ABDC, состоящий из двух треугольников АВС и BCD. Эти треугольники равны по трем сторонам. Таким образом, площадь треугольника ABC равна половине площади параллелограмма ABDC, т.е.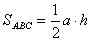

Следствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.

Следствие 2.Если высоты треугольников равны, то их площади относятся друг к другу как основания.

Действительно, если

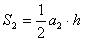и , то, поделив правую часть на правую и левую часть на левую, получим следующее равенство: .

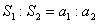Билет№10.

1. Построение отрезка по формуле.
Метод подобия в задачах на построение

В начале этого параграфа мы решим несколько стандартных задач на построение отрезка по заданной формуле. Или, более точно, построение отрезка, длина которого выражается через длины данных отрезков с помощь заданной формулы.

Набор простейших задач, который мы рассмотрим, служит основой алгебраического метода решения задач на построение. Суть метода состоит в том, что данная задача на построение сводится к построению какого-то неизвестного отрезка. Этот отрезок оказывается возможным выразить через известные отрезки и величины. Находится формула, дающая такое выражение. Затем предлагается способ построения отрезка по найденной формуле. Этот способ обычно состоит в том, то, используя стандартный набор построений, мы строим сначала несколько вспомогательных отрезков, а затем уже искомый отрезок.

Построение отрезка по формуле x =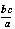

Задача 1.

Даны три отрезка a, b и c. Постройте отрезок x, выражающийся через a, b и c по формуле x = .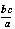

Заметим, то равенство x = 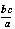эквивалентно равенству = 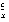, которое означает, что x является четвертым пропорциональным отрезком для отрезков a, b и c.

Решение.Построение основано на теореме о пропорциональных отрезках. На одной стороне произвольного угла от вершины последовательно отложим отрезки a и c, а на другой - отрезок b . Проведем прямую l через концы отрезков a и b, а затем через другой конец отрезка c проведем прямую, параллельную l. Две эти параллельные прямые ограничат примыкающий к b нужный отрезок x. Ведь по указанной теореме 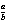= 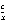. t