Изоморфизм конечномерных векторных пространств
Азн.9.1. V, U-линейные пространства над P. f: V→U- линейное отображение. Когда f - биекция, тогда f называется изоморфизмом.
Пример 9.2. 1) 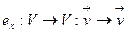 - тождественное отображение. Биективность очевидна. Раньше показано, что линейно. 2)
- тождественное отображение. Биективность очевидна. Раньше показано, что линейно. 2) 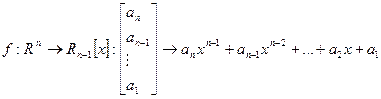 .Биективность очевидна.
.Биективность очевидна.
Св-во 9.3. Когда f:V→U- изоморфизм линейных просторов, тогда f -1: V→U- также изоморфизм линейных просторов. Доказательство. Поскольку f - биекция ,тогда f -1- существует и является биекцией. Надо доказать, что f -1- линейное отображение. 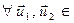 U
U 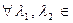 P существуют единственные
P существуют единственные 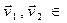 V такие, что
V такие, что 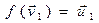 и
и 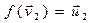 . При этом заметим, что
. При этом заметим, что 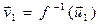 и
и 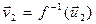 . Тогда
. Тогда 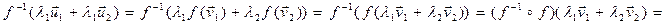
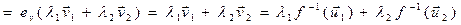 . n
. n
Опр. 9.4. Если существует изоморфизм линейного пространства f:V→U, то говорят, что пространства V и U изоморфны и пишут 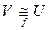 .
.
Теорема 9.5. Отношение быть изоморфными - отношение эквивалентности на множестве линейных просторов
над P. Доказательство. 1) (рефлексивность) V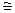 V по 9.2.1; 2) (симметричность) V
V по 9.2.1; 2) (симметричность) V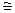 U
U 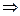 U
U 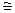 V по 9.3;
V по 9.3;
3) (транзитивность) Пусть V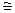 U і U
U і U 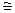 W , а
W , а 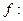 V
V 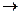 U і
U і 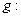 U
U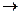 W - соответственные изоморфизмы, тогда отображение
W - соответственные изоморфизмы, тогда отображение 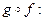 V
V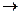 W линейное па 8.11 и является биекцией, как композиция биекций, значиться является изоморфизмом и V
W линейное па 8.11 и является биекцией, как композиция биекций, значиться является изоморфизмом и V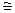 W.n
W.n
Теорема 9.6. Когда dimpV=n, тогда V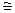 P (изоморфно).Доказательство. Пусть dimpV=n , фиксируем базис
P (изоморфно).Доказательство. Пусть dimpV=n , фиксируем базис 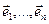 в V. Тогда произвольный
в V. Тогда произвольный 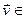 V мои в этом базисе координаты
V мои в этом базисе координаты 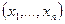 . Зададим отображение f: V→Pn:
. Зададим отображение f: V→Pn: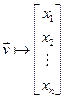 . Поскольку разные векторы в данном базисе имеют разные координаты, f является инъективным отображением. Для произвольного столбца Y=
. Поскольку разные векторы в данном базисе имеют разные координаты, f является инъективным отображением. Для произвольного столбца Y=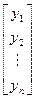
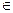 Pn рассмотрим вектор
Pn рассмотрим вектор 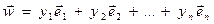 . Очевидно, что
. Очевидно, что 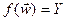 , значиться, отображение f - сюрьективное, из чего следует, что f - биекция. n
, значиться, отображение f - сюрьективное, из чего следует, что f - биекция. n
Следствие 9.7. Все пространства размерности n над полем Р изоморфно. Доказательство: По 9.6. они все изоморфны Р. По 9.5. они изоморфны между собой n