Координаты вектора в базисе. Определение и свойства
Св-во 5.9. Пусть 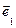 ,
,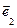 ,. . . ,
,. . . ,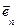 (1) - базис пространства V. Каждый вектор
(1) - базис пространства V. Каждый вектор 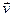 ÎV единственным образом раскладывается по базису, то есть существует единственная последовательность l1, l2, …,lnÎPтакая, что
ÎV единственным образом раскладывается по базису, то есть существует единственная последовательность l1, l2, …,lnÎPтакая, что
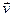 =l1
=l1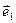 +l2
+l2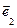 + . . . +ln
+ . . . +ln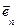 (3) . Доказательство. Существование очевидно из условия полноты. Докажем единственность. Пусть
(3) . Доказательство. Существование очевидно из условия полноты. Докажем единственность. Пусть 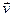 =m1
=m1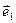 +m2
+m2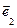 + . . . +mn
+ . . . +mn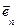 , тогда l1
, тогда l1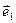 +l2
+l2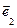 + . . . +ln
+ . . . +ln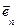 =m1
=m1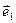 +m2
+m2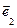 + . . . +mn
+ . . . +mn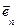 ,значит
,значит
(l1 – m1) 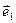 + (l2 – m2)
+ (l2 – m2) 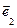 + ... + (ln – mn)
+ ... + (ln – mn) 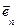 =
=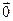 . Из условия линейной независимости получаем, что
. Из условия линейной независимости получаем, что
l1=m1, l2=m2, ... , ln=mn.■
Опр. 5.10. Упорядоченная n-ка (l1;...;ln)из расписания (3) называется координатами вектора 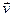 в базисе (1). Координаты вектора записывают в строчку (l1;...;ln)в ли столбец
в базисе (1). Координаты вектора записывают в строчку (l1;...;ln)в ли столбец  .
.
Св-во 5. 11. Когда вектор имеет в базисе (1) столбец координат X=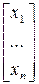 ,тогда "lÎR,вектор l
,тогда "lÎR,вектор l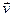 имеет в (1) столбец координат lC=
имеет в (1) столбец координат lC=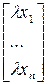 . Доказательство. По условию,
. Доказательство. По условию,  = x1
= x1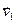 +x2
+x2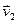 + ... +xn
+ ... +xn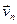 , откуда l
, откуда l =lx1
=lx1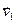 +lx2
+lx2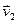 +...+lxn
+...+lxn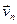 .■
.■
Св-во 5.12. Когда в базисе (1) вектор 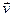 имеет столбец координат X=
имеет столбец координат X= а вектор
а вектор  имеет столбец координат Y=
имеет столбец координат Y=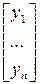 , тогда
, тогда 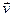 +
+ имеет в этом базисе столбец координат X+Y. Доказательство. По условию,
имеет в этом базисе столбец координат X+Y. Доказательство. По условию, =x1
=x1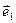 +x2
+x2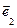 + ... +xn
+ ... +xn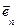 ,
, 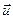 =y1
=y1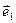 +y2
+y2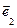 + ... +yn
+ ... +yn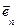 . Тогда,
. Тогда, 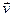 +
+ = (x1
= (x1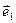 + x2
+ x2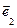 + ... + xn
+ ... + xn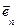 ) + ( y1
) + ( y1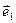 +y2
+y2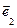 + ... +yn
+ ... +yn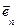 ) =
) =
= (x1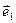 + y1
+ y1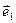 ) + (x2
) + (x2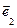 +y2
+y2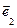 ) + ...+ (xn
) + ...+ (xn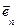 + yn
+ yn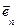 ) = (x1 + y1)
) = (x1 + y1)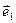 + (x2 + y2)
+ (x2 + y2)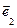 +...+ (xn + yn)
+...+ (xn + yn)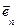 .
. 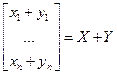 ■
■
В. 5. 13. Когда в базисе (1) векторы 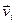 (
(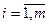 )имеют столбцы координат Xi,, тогда "liÎPвектор
)имеют столбцы координат Xi,, тогда "liÎPвектор 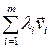 имеет столбец координат
имеет столбец координат 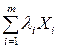 . (Доказательство. ММИ по m.■)
. (Доказательство. ММИ по m.■)