Средняя и предельная ошибки выборки. Теоремы Чебышева - Ляпунова.
Ошибка выборочного наблюдения ‑ это разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения. Для среднего значения ошибка будет определяться так:
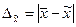 ,
,
где 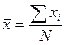 ;
;
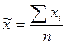
Величина 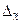 называется предельной ошибкой выборки.
называется предельной ошибкой выборки.
Предельная ошибка выборки величина случайная. Исследованию закономерностей случайных ошибок выборки посвящены предельные теоремы закона больших чисел. Наиболее полно эти закономерности раскрыты в теоремах П. Л. Чебышева и А. М. Ляпунова.
Теорему П.Л. Чебышева применительно к рассматриваемому методу можно сформулировать следующим образом: при достаточно большом числе независимых наблюдений можно с вероятностью, близкой к единице (т.е. почти с достоверностью), утверждать, что отклонение выборочной средней от генеральной будет сколько угодно малым. В теореме П. Л. Чебышева доказано, что величина ошибки не должна превышать 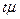 . В свою очередь, величина
. В свою очередь, величина 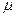 , выражающая среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колеблемости признака в генеральной совокупности
, выражающая среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колеблемости признака в генеральной совокупности 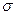 и числа отобранных единиц
и числа отобранных единиц 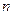 . Эта зависимость выражается формулой:
. Эта зависимость выражается формулой:
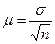 ,
,
где 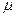 зависит также и от способа производства выборки.
зависит также и от способа производства выборки.
Величину 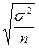 называют средней ошибкой выборки и обозначают
называют средней ошибкой выборки и обозначают 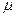 .
.
В этом выражении 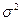 - генеральная дисперсия, n- объем выборочной совокупности.
- генеральная дисперсия, n- объем выборочной совокупности.
А.М. Ляпунов доказал, что распределение выборочных средних (а следовательно, и их отклонений от генеральной средней) при достаточно большом числе независимых наблюдений приближенно нормально при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.
Математически теорему Ляпунова можно записать так:
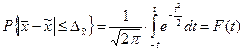 ,
,
где 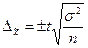 ;
; 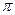 = 3,14 (математическая постоянная);
= 3,14 (математическая постоянная);
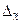 - предельная ошибка выборки, которая дает возможность выяснить, в каких пределах находится величина генеральной средней.
- предельная ошибка выборки, которая дает возможность выяснить, в каких пределах находится величина генеральной средней.
Значения этого интеграла для различных значений коэффициента доверия t вычислены и приводятся в специальных математических таблицах. В частности, при
t = 1 F (t) = 0,683; t = 1,5 F (t) = 0,866;
t = 2 F (t) = 0,954; t = 2,5 F (t) = 0,988;
t = 3 F (t) = 0,997; t = 3,5 F (t) = 0,999.
Поскольку t указывает на вероятность расхождения 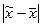 , т.е. на вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней, то это может быть прочитано так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ±
, т.е. на вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней, то это может быть прочитано так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ±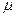 . С вероятностью 0,954 можно утверждать, что ошибка репрезентативности не превышает ±
. С вероятностью 0,954 можно утверждать, что ошибка репрезентативности не превышает ±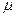 (т. е. в 95% случаев). С вероятностью 0,997, т.е. довольно близкой к единице, можно ожидать, что разность между выборочной и генеральной средней не превзойдет трехкратной средней ошибки выборки и т.д.
(т. е. в 95% случаев). С вероятностью 0,997, т.е. довольно близкой к единице, можно ожидать, что разность между выборочной и генеральной средней не превзойдет трехкратной средней ошибки выборки и т.д.
Логически связь здесь выглядит довольно ясно: чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о ее величине.
Для различных способов отбора предельная ошибка рассчитывается при проведении выборки по-разному.
Зная выборочную среднюю величину признака 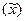 и предельную ошибку выборки
и предельную ошибку выборки 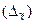 , можно определить границы (пределы), в которых заключена генеральная средняя:
, можно определить границы (пределы), в которых заключена генеральная средняя:
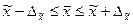 или
или 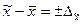
Теорема Бернулли была доказана раньше теоремы Чебышева - Ляпунова, но является лишь частным случаем последней. Она рассматривает ошибку выборки для альтернативного признака, т.е. признака, у которого возможны только два исхода: наличие признака (1) и отсутствие его (0).
Теорема Бернулли утверждает, что при достаточно большом объеме выборки вероятность расхождения между долей признака в выборочной совокупности (w) и долей признака в генеральной совокупности (р) будет стремиться к единице.
Из теоремы Бернулли следует, что величина расхождения между долей признака в выборочной совокупности (частостью) и долей этого признака в генеральной совокупности зависит, так же как и в расхождениях средних, от средней ошибки выборки.
Поскольку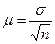 , а среднее квадратическое отклонение в генеральной совокупности для альтернативного признака равно
, а среднее квадратическое отклонение в генеральной совокупности для альтернативного признака равно 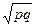 , где
, где 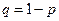 , то средняя ошибка выборки для альтернативного признака будет найдена по формуле:
, то средняя ошибка выборки для альтернативного признака будет найдена по формуле:
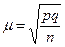 .
.
Однако доля признака в выборочной совокупности нам неизвестна, мы вынуждены заменить ее через долю того же признака в генеральной совокупности, т.е. принять 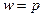 , а дисперсию альтернативного признака принять за
, а дисперсию альтернативного признака принять за 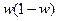 , тогда средняя ошибка выборки выразится формулой:
, тогда средняя ошибка выборки выразится формулой:
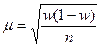 .
.
Предельная величина разности между частостью и долей называется предельной ошибкой выборки. О величине предельной ошибки можно судить с некоторой вероятностью, которая зависит от множителя t, поскольку 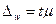 .
.
Зная выборочную долю признака (w) и предельную ошибку выборки 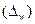 , можно определить границы, в которых заключена генеральная доля (р):
, можно определить границы, в которых заключена генеральная доля (р):
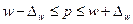 .
.
Уточнение формулы средней ошибки выборки. Если отбор единиц из генеральной совокупности произведен бесповторным способом, то в формулы средней ошибки выборки вносится поправка:
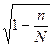 ,
,
где 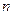 - объем выборочной совокупности;
- объем выборочной совокупности;
N - объем генеральной совокупности.
В таблице 5.2 приведены формулы расчета ошибок простой случайной выборки.
Таблица 5.2 – Формулы ошибок простой случайной выборки
| Наименование ошибки | Способ отбора | |
| повторный | бесповторный | |
Средняя ошибка 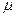 : :
| ||
| для средней | 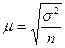
| 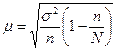
|
| для доли | 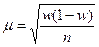
| 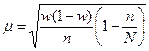
|
Предельная ошибка 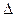 : :
| ||
| для средней | 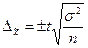
| 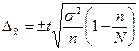
|
| для доли | 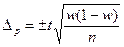
| 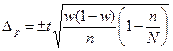
|