Вопрос 5

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

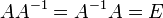
Теорема 4.1 о существовании и единственности обратной матрицы. Квадратная матрица , определитель которой отличен от нуля, имеет обратную матрицу и притом только одну:

 

 

где 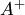— матрица, транспонированная для матрицы, составленной из алгебраических дополнений элементов матрицы .

 

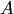Матрица 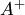называется присоединенной матрицей по отношению к матрице .

 

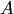В самом деле, матрица 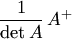существует при условии 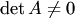. Надо показать, что она обратная к 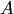, т.е. удовлетворяет двум условиям:

 

Докажем первое равенство. Согласно п.4 замечаний 2.3, из свойств определителя следует, что 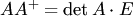. Поэтому

 

что и требовалось показать. Аналогично доказывается второе равенство. Следовательно, при условии 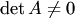матрица 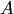имеет обратную

 

 

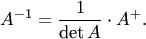
Единственность обратной матрицы докажем от противного. Пусть кроме матрицы 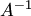существует еще одна обратная матрица 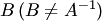такая, что 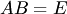. Умножая обе части этого равенства слева на матрицу 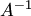, получаем 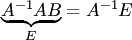. Отсюда 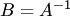, что противоречит предположению 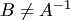. Следовательно, обратная матрица единственная.