Факторно-регрессионные модели характеристик электрических станций

 

Задача оптимизации размещения и выбора мощности электрических станций предполагает наличие экономических показателей их сооружения. При решении оптимизационных задач или задач сравнительной эффективности вариантов развития энергетических объектов в качестве экономического критерия обычно используются затраты. Затраты могут быть представлены в виде зависимости от совокупности технико-экономических показателей, включая постоянные (K^пост_уд) и переменные (K^пер_уд) удельные капиталовложения в сооружение электрических станций и другие экономические показатели (Э_ст),

 

З = f (K^пост_уд, K^пер_уд, Э_ст ). (161)

Постоянные удельные капиталовложения K^пост_удпрактически не зависят от местоположения электростанции и определяются, в основном, конкретными технико-экономическими параметрами такими как тип и мощность электростанции, число и мощность блоков, система технического водоснабжения, вид топлива и другие, образующие первый информационный уровень (Х_I). В связи с тем, что размер совокупности параметров первого информационного уровня не очень велик и составляет около десяти параметров, моделирование постоянных удельных капиталовложений K^пост_уд обычно выполняется на основе прямого использования методов регрессионного моделирования,

K^пост_уд = f (Х₁). (162)

Формирование переменных удельных капиталовложений K^пер_уд во многом определяется региональными (Х_II) и местными или локальными (Х_III) инженерно-географическими условиями сооружения электрических станций, характеризующимися информационными параметрами, образующими второй и третий информационные уровни,

K^пер_уд = f (Х_II, Х_III) . (163)

Сложность задачи моделирования переменных удельные капиталовложения K^пер_уд объясняется свойствами параметров второго и третьего информационных уровней.

1. Размерность совокупности параметров второго и третьего информационных уровней весьма значительна и составляет около сотни параметров. Следует отметить, что статистическая достоверность моделей достигается лишь в том случае, когда размер обучающей выборки превышает размерность совокупности параметров примерно на порядок. При моделировании же переменных удельных капиталовложений размер обучающей выборки N ограничен числом выполненных проектов, ТЭО электростанций и составляет величину того же порядка, что и размер совокупности параметров Х_IIиХ_III.

2. Каждый отдельный параметр второго и третьего информационных уровней имеет довольно слабые связи с моделируемыми переменными удельными капиталовложениями, в то же время совместное влияние всех параметров второго и третьего информационных уровней велико. В обследованных выборочных совокупностях совместное влияние всех параметров второго и третьего информационных уровней определяет около 80-90% вариации (дисперсии) переменных удельных капиталовложенийK^пер_уд.

3. Параметры второго и третьего информационных уровней взаимозависимы, коррелированны между собой. Некоторые коэффициенты корреляции в обследованных выборочных совокупностях превышают значение 0.8. В то же время регрессионные модели, полученные по коррелированной совокупности параметров, обладают слабой достоверностью (низкой точностью).

Перечисленные свойства параметров второго и третьего информационных уровней ограничивают использование прямого регрессионного анализа для моделирования переменных удельных капиталовложений и обуславливают необходимость предварительного применения методов ортогонального преобразования пространства.

Одним из таких методов является метод факторного анализа. С помощью факторного анализа при моделировании переменных удельных капиталовложений K^пер_удв сооружение электростанций коррелированное пространство параметров второго и третьего информационных уровней (Х_II , Х_III) размерности (n) может быть преобразовано в пространство ортогональных факторов (F) той же размерности (n). При этом, практически без потери точности описания совокупности параметров, размерность пространства факторов может быть существенно снижена до (m), причем (m<<n). Снижение размерности ортогонального пространства факторов позволяет повысить достоверность результатов моделирования переменных удельных капиталовложений K^пер_уд, так как при снижении размерности пространства факторов по сравнению с пространством параметров размер выборочной совокупности не меняется и число наблюдений N становится больше числа переменных m.

Суть метода факторного анализа можно продемонстрировать на примере преобразования пространства двух коррелированных параметров Х₁иХ₂ в пространство ортогональных факторов F₁ и F₂ (см. рисунок 31).

Пусть имеются выборочные совокупности коррелированных параметров Х₁ = {х₁₁, х₁₂, .. х_1i, .. х_1N} и Х₂ = {х₂₁, х₂₂, .. х_2i, .. х_2N}. Выборочные совокупности сформированы случайным образом, поэтому параметры х_1i и х_2iраспределены вокруг своих математических ожиданий по нормальному закону.

Перейдем от именованных параметров Х₁ и Х₂ к нормированным Z₁ и Z₂ :

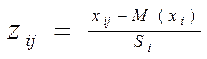, (164)

где i=1,...,n; j=1,...,N .

Следует отметить, что математическое ожидание каждого нормированного параметра равно нулю, а дисперсия единице. Если выборочная совокупность содержит n нормированных параметров, то суммарная дисперсия совокупности нормированных параметров будет равна числу параметров n. В пространстве нормированных параметров Z₁ и Z₂ выборочные значения параметров образуют, как показано на рисунке 31, облако наблюдений по виду близкое к эллипсу (в многомерном случае к гиперэллипсоиду).

При направлении первого фактора F₁вдоль главной, большей оси эллипса, первый фактор будет определять большую часть дисперсии нормированных параметров Z₁ и Z₂. В общем случае, это направление не совпадает с осями Z и это значит, что параметры Х₁ и Х₂ (Z₁ и Z₂) коррелированны между собой.

Второй фактор F₂направляется по меньшей оси эллипса и определяет оставшуюся часть дисперсии нормированных параметров Z₁ и Z₂.

В связи с тем, что первый фактор концентрирует в себе большую часть дисперсии параметров, для описания исходной совокупности параметров Z₁ и Z₂ достаточно выделения одного фактора. Таким образом, исходная коррелированная совокупность двух параметров n=2заменена ортогональной совокупностью факторов размерностью m =1.

Теперь, вместо модели

 

K^пер_уд = а₀ + а₁ х₁ + а₂ х₂ , (165)

может быть построена модель

 

K^пер_уд = b₀ + b₁ f ₁. (166)

 

При большей размерности совокупности параметров n>2 бывает недостаточно учета только одного фактора и следует учесть m факторов, но обычно m<<n.

В общем случае исходное пространство n нормированных коррелированных параметров Z может быть преобразовано в ортогональное пространство факторов F той же размерности n, но при этом первые m факторов (m<<n) , как правило, достаточно полно отражают исходное пространство параметров.

Матрица нормированных параметров Z имеет ту же размерность nN, что и выборочная совокупность именованных параметров X (N-размер выборки наблюдений, n-число параметров),

Z = .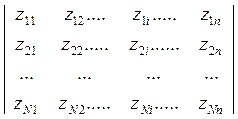

Целью ортогонального преобразования пространства является корректная замена матрицы нормированных параметров Z на матрицу факторов F той же размерности,

F =.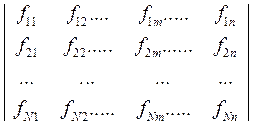

 

Связь между матрицей нормированных параметров Z и матрицей ортогональных факторов F описывается матрицей нагрузок А на факторы размера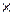 nn,

 

A = .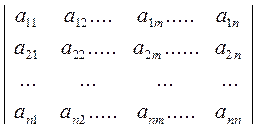

Для каждого отдельного наблюдения к=1,...,N связь вектора параметров 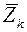c вектором факторов 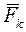в координатной форме имеет вид:

z_k1 = a₁₁f_k1 + a₁₂f_k2 + a₁₃f_k3 +…+ a_1mf_km +…+ a_1nf_kn,

z_k2 = a₂₁f_k1 + a₂₂f_k2 + a₂₃f_k3 +…+ a_2mf_km +…+ a_2nf_kn, (167)

_{. . . . . . . .}

z_kn = a_n1f_k1 + a_n2f_k2 + a_n3f_k3 +…+ a_nmf_km +…+ a_nnf_kn.

В матричном виде связь нормированных параметров с факторами имеет вид:

Z=AF. (168)

Для оценки коэффициентов матрицы нагрузок А используется матрица выборочных коэффициентов парной корреляции параметров R. Каждый из коэффициентов r_ij матрицы определяется в зависимости от нормированных параметров:

,

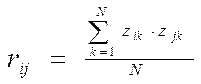где i,j=1,…,n.

Выражение (168) можно записать в матричном виде:

 

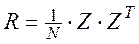. (169)

Матрица нагрузок связана с выборочной корреляционной матрицей соотношением:

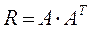.(170)

Для обоснования формулы (170) достаточно умножить обе части выражения (168) на их транспонированные значения,

 

,

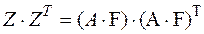тогда

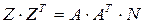. (171)

 

Выразив правую часть соотношения (171) с использованием выражения (169) можно получить выражение (170):

 

.

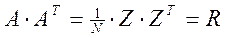Коэффициенты матрицы нагрузок А находятся на основе собственных значений (чисел) 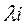и проекций собственных векторов 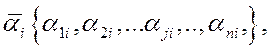i,j=1,2,3,…,m,…,n, корреляционной матрицы R выборочных значений параметров по выражению:

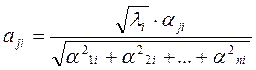. (172)

С целью определения собственных значений (чисел) 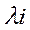и проекций собственных векторов , составляется характеристическое уравнение для корреляционной матрицы в виде:

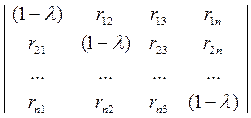= 0 . (173)

 

Корни характеристического уравнения и есть собственные числа матрицы R. Если матрица неособенная, а R-именно такая, и её ранг равен её размерности, то собственные числа матрицы положительны (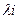>0), количество собственных чисел и их сумма равны размерности матрицы n,

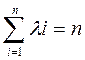. (174)

Как видно сумма корней характеристического уравнения – собственных чисел корреляционной матрицы равна суммарной дисперсии выборочной совокупности нормированных параметров и, следовательно, собственные числа могут служить оценкой дисперсии параметров. Если расположить собственные числа корреляционной матрицы 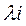в порядке их убывания так, чтобы 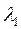>>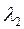…>>…>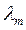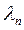, то первое собственное число будет описывать максимальную долю дисперсии совокупности параметров, а каждое последующее меньшую долю. Анализ значений собственных чисел 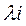показывает, что сумма первых m собственных чисел практически равна n, а остальные собственные числа несопоставимо малы и могут быть отброшены,

.

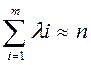Это означает, что первые m собственных чисел могут служить оценкой дисперсии всей совокупности параметров.

Далее возникает задача определения собственных векторов корреляционной матрицы, соответствующих первым m собственным числам 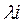. Расчет векторов корреляционной матрицы ведется в порядке убывания собственных чисел, то есть вначале находится собственный вектор, соответствующий максимальному собственному числу 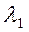, затем следующим по величине .

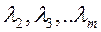Для оценки проекций собственного вектора 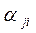, где j=1,2,…,n , i=1,2,…,m составляется система линейных уравнений вида

 

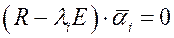, (175)

здесь Е - единичная матрица, 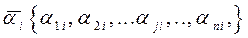- собственный вектор с номером i.

Выражение (175) можно представить в координатной форме:

 

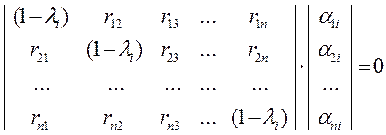(176)

 

Система линейных уравнений (176) включает два линейно зависимых уравнения (так как 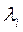– являются корнями характеристического уравнения корреляционной матрицы R). Системы линейно зависимых уравнений имеют множество решений, поэтому для получения проекций собственного вектора 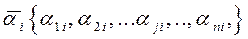необходимо предварительно как-то ориентировать одну из проекций вектора 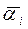и понизить размерность системы уравнений. Задав одну из проекций 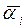, можно определить остальные координаты вектора на основе решения системы уравнений меньшей размерности.

Первый собственный вектор 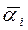, соответствующий максимальному собственному значению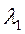, указывает направление первого фактора, а его длина определяется значением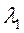. Теперь коэффициенты матрицы нагрузок А можно найти на основе собственных значений корреляционной матрицы 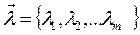и соответствующих им собственных векторов 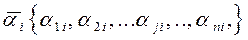по выражению (172).

Как уже было указано выше, суммарная дисперсия совокупности n нормированных параметров равна размерности совокупности n. Учет факторами 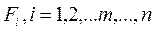суммарной дисперсии нормированных параметров определяется соответствующими собственными числами 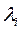корреляционной матрицы, сумма которых равна n. Следовательно, если сумма первых m собственных чисел примерно равно n, тогда и первые m (m<n) факторов учитывают почти всю дисперсию n параметров.

Вклад каждого фактора в дисперсию параметров соответствует величине 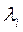, так как сумма дисперсий нормированных параметров равна их сумме, то есть n, учет суммарной дисперсии параметров первыми m факторами показан на рисунке 32.

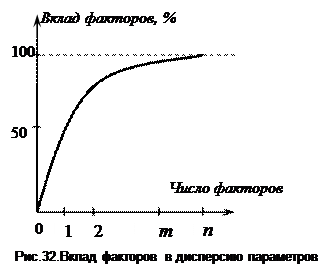
На основе анализа учета факторами суммарной дисперсии совокупности нормированных параметров можно отбросить несущественные факторы с номерами i = m+1, m=2,…n и получить редуцированную (усеченную) матрицу А.

 

.

 

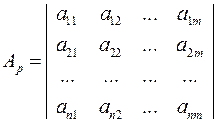Для оценки учета дисперсии совокупности нормированных параметров первыми m выделенными факторами используется матрица вычисленных коэффициентов корреляции .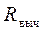

Матрицу вычисленных коэффициентов корреляции 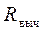можно определить по выражению (10) с использованием редуцированной матрицы нагрузок на факторы,

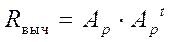. (177)

Проверку достаточности числа выделенных факторов m необходимо проверить по статистическим критериям. В качестве статистического критерия может быть использован критерий Пирсона. По критерию Пирсона оценивается значимость коэффициентов матрицы остаточных коэффициентов корреляции 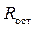. Матрица остаточных коэффициентов корреляции 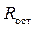вычисляется как разность матриц выборочных и вычисленных коэффициентов корреляции параметров,

 

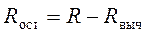. (178)

Для оценки значимости матрицы остаточных коэффициентов корреляции 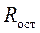определяется матрица доверительных интервалов коэффициентов корреляции 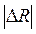, состоящая из доверительных интервалов для каждого коэффициента корреляции 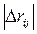. Доверительные интервалы коэффициентов корреляции 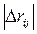определяются с использованием стандартного статистического распределения Пирсона.

Принцип проверки значимости матрицы остаточных коэффициентов корреляции заключается в сравнении каждого коэффициента матрицы 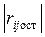с его доверительным интервалом. Коэффициент считается незначимым если соблюдается условие 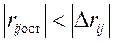для каждого коэффициента матрицы 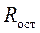или для всей матрицы остаточных коэффициентов корреляции 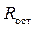в целом,

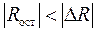. (179)

Если проверка значимости матрицы остаточных коэффициентов корреляции неудовлетворительна, то следует увеличить число выделяемых факторов. Процесс увеличения числа факторов продолжается до тех пор, пока остаточные коэффициенты корреляции значимы.

После выделения достаточного числа ортогональных факторов следует приступить к оценке значений факторов по всем наблюдениям выборочной совокупности нормированных параметров. Значения m выделенных факторов по N наблюдениям образуют матрицу факторов F.

Оценка значений факторов по наблюдениям производится с помощью регрессионного анализа. С этой целью левая и правая части выражения (168) умножаются на их транспонированные значения:

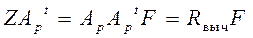. (180)

Теперь, обратив матрицу вычисленных коэффициентов корреляции и преобразовав выражение (180), можно получить матрицу значений факторов по наблюдениям

,

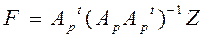или

F= W Z, (181)

 

где W –матрица связи параметров с факторами,

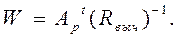(182)

 

После оценки значений факторов по наблюдениям можно на основе регрессионного анализа построить факторно-регрессионную модель переменных удельных капиталовложений в сооружение электрических станций в зависимости от ортогональных факторов в виде

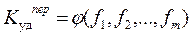. (183)

 

Факторно-регрессионные модели переменных удельных капиталовложений в сооружение электрических станций в зависимости от ортогональных факторов обладают приемлемой точностью и могут быть использованы при решении задач развития электроэнергетических систем. Следует заметить, что при использовании факторно-регрессионных моделей для прогнозирования технико-экономических характеристик необходимо предварительно определить на перспективу прогнозные значения факторов. Обычно при определении прогнозных значений факторов не выполняется уточнение матрицы связи W и используется матрица связи, полученная по обучающей выборке параметров.