Интервальная оценка математического ожидания.

2.1. Интервальная оценка математического ожидания при известной дисперсии

 

Итак, Х ~ N(а,σ) (случайная величина Х имеет нормальное распределение с параметрами а и σ), причем значение параметра а не известно, а значение дисперсии σ² известно.

При 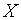~ 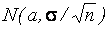эффективной оценкой параметра а является 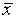, при этом 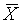~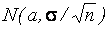. Статистика 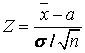имеет распределениеN(0; 1) независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна. Следовательно, с учетом неравенства (1.12) и симметричности двусторонних критических границ распределения N(0; 1) будем иметь:

Р(–u_а < Z < u_а) = 1 – α = γ.

Решая неравенство 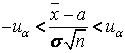относительно а, получим, что с вероятностью 1 – α выполняется неравенство

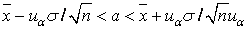, (1.13)

 

при этом

 

. (1.14)

 

Число u_а находят по прил. 3 из условия Ф(u_а) = γ/2.

Замечание. Если п велико, оценку (1.13) можно использовать и при отсутствии нормального распределения величины Х, так как в силу следствия из центральной предельной теоремы при случайной выборке большого объема п

.

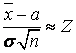В частности, если Х = μ, где μ – случайное число успехов в большом числе п испытаний Бернулли, то

,

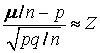и с вероятностью ≈1 – α для вероятности р успеха в единичном испытании выполняется неравенство

 

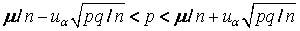. 1.15)

 

Заменяя значения р и q = 1 – р в левой и правой частях неравенства (1.15) их оценкам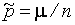и и 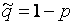, что допустимо при большом п,получим приближенный доверительный интервал для вероятности р:

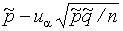< p < 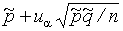. (1.16)