рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Понятие о статистической оценке параметров
Реферат Курсовая Конспект
Понятие о статистической оценке параметров
Понятие о статистической оценке параметров - раздел Образование, 1. Понятие О Статистической Оценке Параметров. Пробл...
1. Понятие о статистической оценке параметров.
Проблемы статистических выводов традиционно делятся на проблемы оценивания и проверку гипотез. Главное различие между этими двумя проблемами состоит в том, что при оценивании мы должны определить величину параметра или нескольких параметров. В то время как при проверке гипотез мы должны решить: принять или отвергнуть специфическую величину (или ряд специфических величин) параметра или нескольких параметров.
В общем виде задача оценки параметров формулируется следующим образом.
Пусть распределение признака Х - генеральной совокупности - задается функцией вероятности f(x, θ) = P(X=xi) для дискретной случайной величины или плотностью вероятностей для непрерывной случайной величины, которая содержит неизвестный параметр θ.
Для вычисления параметра θ используют выборку x1, x2, ..., xn, каждая из которых имеет один и тот же закон распределения, что и признак Х.
Оценкой θn параметра θ называют всякую функцию результатов наблюдений (иначе - статистику), с помощью которой делают вывод о значении параметра θ:
θn = θn(x1, x2, ..., xn).
Так как x1, x2, ..., xn - случайные величины, то и оценка θn является случайной величиной, которая зависит от закона распределения и объема выборки n. Оцениваемый параметр θ является постоянной величиной.
Всегда существует множество функций от результатов наблюдений x1, x2, ...xn, которые можно предложить в качестве оценки параметра θ. Например, для математического ожидания в качестве оценки θn по выборке можно взять среднюю арифметическую результатов наблюдений , моду M0, медиану Me и т. д.
Какими свойствами должна обладать оценка θn?
Так как θn - случайная величина, то невозможно предсказать индивидуальное значение оценки в данном частном случае. Поэтому о качестве оценки следует судить не по ее индивидуальным значениям, а по распределению ее значений при достаточно большом числе испытаний, т. е. по выборочному распределению оценки.
2.2.2. Наиболее важные свойства оценок
Оценка θn параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е.
M(θn) = θ.
В противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка θn, полученная по разным выборкам, будет либо завышать θ, если M(θn) > θ, либо занижать его, если M(θn) < θ. Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Являются ли оценки математического ожидания μ и дисперсии σ 2 несмещенными?
Для матожидания оценкой, полученной по выборке, является среднее арифметическое :
,
что говорит о том, что - несмещенная оценка для матожидания.
Для дисперсии σ 2 оценкой, полученной по выборке, является S 2:
так как в случае независимых и одинаково распределенных с дисперсией σ 2 наблюдений x1, x2, ..., xn имеем
(см. свойства дисперсии).
Для устранения смещения в оценке дисперсии достаточно оценку S 2 домножить на , тогда несмещенной оценкой генеральной дисперсии будет выборочная дисперсия
.
Коэффициент особенно важен для выборок малого объема.
Для оценок важными являются еще свойства состоятельности и эффективности, определения которых приводятся ниже.
Оценка θn параметра θ называется состоятельной, если она удовлетворяет закону больших чисел, т. е. сходится по вероятности к оцениваемому параметру
или
.
Если оценка состоятельна, то практически достоверно, что при достаточно большом n θn ≈ θ.
Несмещенная оценка θn параметра θ является эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема n. Так как для несмещенной оценки M(θn – θ)2 есть дисперсия , то эффективность является решающим свойством, определяющим качество оценки.
В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.
Для случайной величины Х, распределенной по нормальному закону, среднее арифметическое является несмещенной, состоятельной и эффективной оценкой для математического ожидания.
2. Распределение средней арифметической. Распределение Стьюдента. Их применение в математической статистике.
Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма Сили Госсета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент».
Определение
Пусть 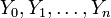 — независимые стандартные нормальные случайные величины, такие что
— независимые стандартные нормальные случайные величины, такие что 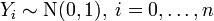 . Тогда распределение случайной величины
. Тогда распределение случайной величины 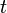 , где
, где
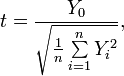
называется распределением Стьюдента с 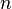 степенями свободы. Пишут
степенями свободы. Пишут 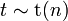 . Её распределение абсолютно непрерывно и имеет плотность
. Её распределение абсолютно непрерывно и имеет плотность
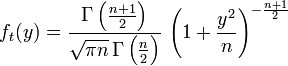 ,
,
где 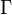 — гамма-функция Эйлера.
— гамма-функция Эйлера.
Свойства распределения Стьюдента
· Распределение Стьюдента симметрично. В частности если 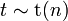 , то
, то 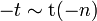 .
.
Моменты
Случайная величина 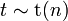 имеет только моменты порядков
имеет только моменты порядков 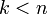 , причём
, причём
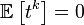 , если
, если 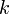 нечётно;
нечётно;
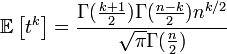 , если
, если 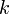 чётно.
чётно.
В частности,
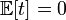 ,
,
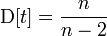 , если
, если 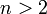 .
.
Моменты порядков 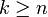 не определены.
не определены.
Связь с другими распределениями
· Распределение Коши является частным случаем распределения Стьюдента: 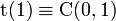 .
.
· Распределение Стьюдента сходится к стандартному нормальному при 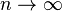 . Пусть дана последовательность случайных величин
. Пусть дана последовательность случайных величин 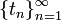 , где
, где 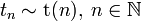 . Тогда:
. Тогда: 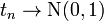 по распределению при
по распределению при 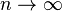 .
.
· Квадрат случайной величины, имеющей распределение Стьюдента, имеет распределение Фишера. Пусть 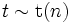 . Тогда:
. Тогда: 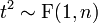 .
.
Применение распределения Стьюдента
Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения. В частности, пусть 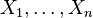 независимые случайные величины, такие что
независимые случайные величины, такие что 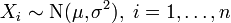 . Обозначим
. Обозначим 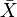 выборочное среднее этой выборки, а
выборочное среднее этой выборки, а 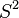 её выборочную дисперсию. Тогда
её выборочную дисперсию. Тогда
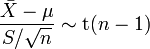 .
.
- Распределения Пирсона (χ2) и Фишера-Снедекора. Их применение в математической статистике.
Распределение "хи-квадрат"
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. Это распределения Пирсона ("хи – квадрат"), Стьюдента и Фишера.
Мы остановимся на распределении 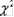 ("хи – квадрат"). Впервые это распределение было исследовано астрономом Ф.Хельмертом в 1876 году. В связи с гауссовской теорией ошибок он исследовал суммы квадратов n независимых стандартно нормально распределенных случайных величин. Позднее Карл Пирсон (Karl Pearson) дал имя данной функции распределения "хи – квадрат". И сейчас распределение носит его имя.
("хи – квадрат"). Впервые это распределение было исследовано астрономом Ф.Хельмертом в 1876 году. В связи с гауссовской теорией ошибок он исследовал суммы квадратов n независимых стандартно нормально распределенных случайных величин. Позднее Карл Пирсон (Karl Pearson) дал имя данной функции распределения "хи – квадрат". И сейчас распределение носит его имя.
Благодаря тесной связи с нормальным распределением, χ2-распределение играет важную роль в теории вероятностей и математической статистике. χ2-распределение, и многие другие распределения, которые определяются посредством χ2-распределения (например - распределение Стьюдента), описывают выборочные распределения различных функций от нормально распределенных результатов наблюдений и используются для построения доверительных интервалов и статистических критериев.
Распределение Пирсона 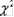 (хи - квадрат) – распределение случайной величины
(хи - квадрат) – распределение случайной величины 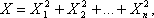 где X1, X2,…, Xn - нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение - единице.
где X1, X2,…, Xn - нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение - единице.
Сумма квадратов
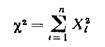
распределена по закону 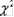 ("хи – квадрат").
("хи – квадрат").
При этом число слагаемых, т.е. n, называется "числом степеней свободы" распределения хи – квадрат. C увеличением числа степеней свободы распределение медленно приближается к нормальному. Плотность этого распределения
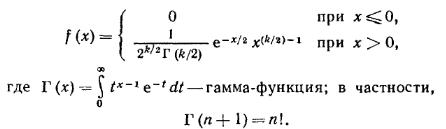
Итак, распределение χ2 зависит от одного параметра n – числа степеней свободы.
Функция распределения χ2 имеет вид:
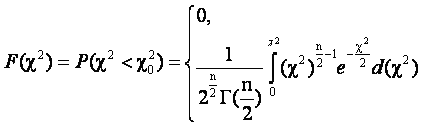
если χ2≥0. (2.7.)
На Рисунок 1 изображен график плотности вероятности и функции χ2 – распределения для разных степеней свободы.
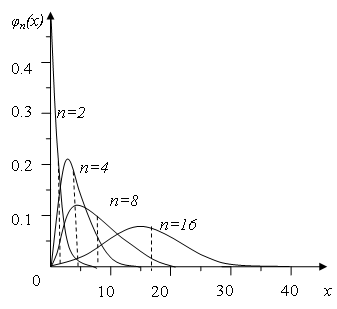
Рисунок 1 Зависимость плотности вероятности φ (x) в распределении χ2 (хи – квадрат) при разном числе степеней свободы.
Моменты распределения "хи-квадрат":
M[χ2]=n
D[χ2]=2n
Распределение "хи-квадрат" используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.
2. "Хи-квадрат" в задачах статистического анализа данных
Статистические методы анализа данных применяются практически во всех областях деятельности человека. Их используют всегда, когда необходимо получить и обосновать какие-либо суждения о группе (объектов или субъектов) с некоторой внутренней неоднородностью.
Современный этап развития статистических методов можно отсчитывать с 1900 г., когда англичанин К. Пирсон основал журнал "Biometrika". Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.
Распределение "хи-квадрат" является одним из наиболее широко используемых в статистике для проверки статистических гипотез. На основе распределения "хи-квадрат" построен один из наиболее мощных критериев согласия – критерий "хи-квадрата" Пирсона.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Критерий χ2 ("хи-квадрат") используется для проверки гипотезы различных распределений. В этом заключается его достоинство.
Расчетная формула критерия равна
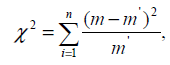
где m и m’ - соответственно эмпирические и теоретические частоты
рассматриваемого распределения;
n - число степеней свободы.
Для проверки нам необходимо сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
При полном совпадении эмпирических частот с частотами, вычисленными или ожидаемыми S (Э – Т) = 0 и критерий χ2 тоже будет равен нулю. Если же S ( Э – Т) не равно нулю это укажет на несоответствие вычисленных частот эмпирическим частотам ряда. В таких случаях необходимо оценить значимость критерия χ2, который теоретически может изменяться от нуля до бесконечности. Это производится путем сравнения фактически полученной величины χ2ф с его критическим значением (χ2st).Нулевая гипотеза, т. е. предположение, что расхождение между эмпирическими и теоретическими или ожидаемыми частотами носит случайный характер, опровергается, если χ2ф больше или равно χ2st для принятого уровня значимости (a) и числа степеней свободы (n).
Распределение вероятных значений случайной величины χ2 непрерывно и ассиметрично. Оно зависит от числа степеней свободы (n) и приближается к нормальному распределению по мере увеличения числа наблюдений. Поэтому применение критерия χ2 к оценке дискретных распределений сопряжено с некоторыми погрешностями, которые сказываются на его величине, особенно на малочисленных выборках. Для получения более точных оценок выборка, распределяемая в вариационный ряд, должна иметь не менее 50 вариантов. Правильное применение критерия χ2 требует также, чтобы частоты вариантов в крайних классах не были бы меньше 5; если их меньше 5, то они объединяются с частотами соседних классов, чтобы в сумме составляли величину большую или равную 5. Соответственно объединению частот уменьшается и число классов (N). Число степеней свободы устанавливается по вторичному числу классов с учетом числа ограничений свободы вариации.
Так как точность определения критерия χ2 в значительной степени зависит от точности расчета теоретических частот (Т), для получения разности между эмпирическими и вычисленными частотами следует использовать неокругленные теоретические частоты.
В качестве примера возьмем исследование, опубликованное на сайте, который посвящен применению статистических методов в гуманитарных науках.
Критерий "Хи-квадрат" позволяет сравнивать распределения частот вне зависимости от того, распределены они нормально или нет.
Под частотой понимается количество появлений какого-либо события. Обычно, с частотой появления события имеют дело, когда переменные измерены в шкале наименований и другой их характеристики, кроме частоты подобрать невозможно или проблематично. Другими словами, когда переменная имеет качественные характеристики. Так же многие исследователи склонны переводить баллы теста в уровни (высокий, средний, низкий) и строить таблицы распределений баллов, чтобы узнать количество человек по этим уровням. Чтобы доказать, что в одном из уровней (в одной из категорий) количество человек действительно больше (меньше) так же используется коэффициент Хи-квадрат.
Фишера F-распределение (F-распределение, Фишера-Снедекора распределение, Снедекора распределение) — непрерывное сосредоточенное на 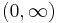 распределение вероятностей с плотностью
распределение вероятностей с плотностью
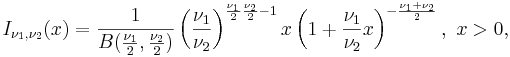
где ν1 > 0 и ν2 > 0 — параметры, а 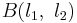 — бета-функция.
— бета-функция.
| Оглавление [Скрыть] 1 Свойства 2 Значение 3 Исторический очерк 4 Литература 5 См. также |
[редактировать]
Свойства
При ν1 > 2 — унимодальное (одновершинное) с положительной асимметрией распределение с модой в точке
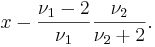
Математическое ожидание и дисперсия равны соответственно
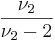 при ν2 > 2,
при ν2 > 2,
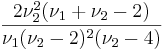 при ν2 > 4.
при ν2 > 4.
Cводится к бета-распределению 2-го рода (распределению типа VI по классификации Пирсона); также можно рассматривать как распределение случайной величины, представимой в форме отношения 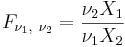 , где независимые случайные величины X1 и X2 имеют гамма-распределения с параметрами
, где независимые случайные величины X1 и X2 имеют гамма-распределения с параметрами 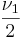 и
и 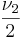 соответственно.
соответственно.
Функция распределения для 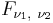 выражается через функцию распределения
выражается через функцию распределения 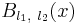 бета-распределения:
бета-распределения:
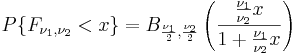 .
.
Это соотношение используется для вычисления значений F-распределения с помощью таблиц бета-распределения.
Если ν1 = m и ν2 = n целые, то F-распределением Фишера с m и n степенями свободы называется распределение F-отношения 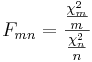 , где
, где 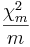 и
и 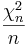 —независимые случайные величины, имеющие хи-квадрат-распределения с m и n степенями свободы соответственно.
—независимые случайные величины, имеющие хи-квадрат-распределения с m и n степенями свободы соответственно.
[редактировать]
Значение
Играет фундаментальную роль в математической статистике и появляется в первую очередь как распределение отношения двух выборочных дисперсий. Именно, пусть X1,...,Xmи Y1,...,Yn — выборки из нормальных совокупностей с параметрами 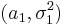 и
и 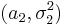 .
.
Выражения
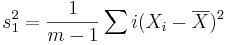 и
и
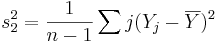 ,
,
где 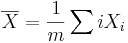 и
и 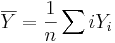 служат оценками дисперсий
служат оценками дисперсий 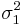 и
и 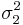 . Тогда так называемое дисперсионное отношение
. Тогда так называемое дисперсионное отношение 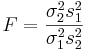 имеет при гипотезе σ1 − σ2 F-распределение с m − 1 и n − 1 степенями свободы (в этом качестве его называют также распределением дисперсионного отношения). На статистике F основан F-критерий, используемый, в частности, для проверки гипотезы равенства дисперсий двух совокупностей, в дисперсионном анализе, регрессионном анализе, многомерном статистическом анализе.
имеет при гипотезе σ1 − σ2 F-распределение с m − 1 и n − 1 степенями свободы (в этом качестве его называют также распределением дисперсионного отношения). На статистике F основан F-критерий, используемый, в частности, для проверки гипотезы равенства дисперсий двух совокупностей, в дисперсионном анализе, регрессионном анализе, многомерном статистическом анализе.
Универсальность F-распределения подчеркивается связями с другими распределениями. При m = 1 квадрат величины Fmn имеет Стьюдента распределение (t-распределение) сn степенями свободы. Существуют различные аппроксимации F-распределения с помощью нормального распределения и хи-квадрат распределения.
4. Точечные оценки. Основные свойства точечных оценок.
Точечные оценки, их свойства, примеры
Определение 1. Выборка -- последовательность результатов измерений значений случайной величины.
Определение 2. Статистическая оценка -- приближенное значение вероятностных характеристик законов распределения, полученных на основе статистических или выборочных данных. Точечная статистическая оценка -- статистическая оценка, выражаемая одним числом.
Определение 3. Статистическая оценка называется несмещенной, если 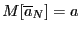 .
.
Определение 4. Точечная оценка называется состоятельной, если 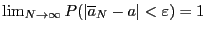 .
.
Определение 5. Точечная оценка называется сильно состоятельной, если 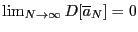 .
.
Определение 6. Точечная оценка 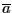 называется эффективной, если
называется эффективной, если 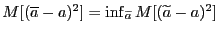 , где
, где 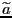 -- все возможные точечные оценки.
-- все возможные точечные оценки.
Определение 7. Точечная оценка называется асимптотически эффективной, если
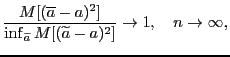
где 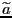 -- все возможные точечные оценки.
-- все возможные точечные оценки.
Пример: выборочное математическое ожидание. 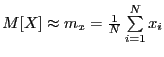 .
.
Определение 8. Пусть 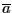 -- оценка параметра
-- оценка параметра 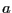 . Мы хотим, чтобы
. Мы хотим, чтобы 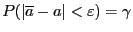 , т.е. чтобы она была достаточно хорошей, была очень близка к реальному значению в очень большом количестве случаев (95%, 99%). Тогда
, т.е. чтобы она была достаточно хорошей, была очень близка к реальному значению в очень большом количестве случаев (95%, 99%). Тогда 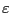 -- точность,
-- точность, 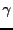 -- надежность.
-- надежность.
5. Точечные оценки основных параметров распределения.
Определения и основные свойства точечных оценок
Задача оценивания параметров распределения генеральной – одна из основных задач математической статистики. На содержательном уровне задача оценивания параметров распределения формулируется так: располагая выборкой реализаций случайной величины Х, необходимо получить оценку 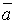 неизвестного параметра генеральной совокупности а и ее статистические свойства.
неизвестного параметра генеральной совокупности а и ее статистические свойства.
Оценивание параметров распределения осуществляется в два этапа. На первом этапе, на основании выборки х1, х2, ... , ,хn ,строится статистика
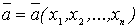 ,
,
значение которой при данной выборке х1, х2, ... , ,хn принимают за приближенное значение оцениваемого параметра а :
а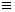
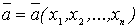 .
.
Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку 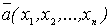 называют точечной.
называют точечной.
Для получения точечной оценки существует много статистик, которые могут быть использованы в качестве оценок. Поэтому второй этап оценивания состоит в выборе наилучшей оценки, что требует введения критерия качества получаемых оценок. Задача усложняется тем, что ввиду малого объема выборки требуется статистический подход к качеству оценки
По опытным данным (выборке) путем построения гистограммы или с помощью других средств можно попытаться выбрать вероятностную модель (определить закон распределения генеральной совокупности). При этом выборочные данные позволяют уточнить детали вероятностной модели. Знание вероятностной модели дает возможность прогнозировать будущие события, что важно для принятия решений. В приложениях обычно задаются определенным типом закона распределения генеральной совокупности (плотностью распределения)
f = f(x; a1, a2, ..., am)
и по данным случайной выборки х1, х2, ..., хn оценивают неизвестные параметры a1, a2, ..., am . Чаще всего параметрами являются генеральное среднее и дисперсия, а качестве оценки тогда используют выборочные характеристики: выборочное среднее и выборочную дисперсию.
Рассмотрим следующую задачу. Пусть имеется случайная величина Х и нам известен ее закон распределения f = f(x, a), который содержит один неизвестный параметр а. Требуется на основании выборочных данных х1, х2, ..., хn найти подходящую оценку параметра а. Для решения этой задачи построим следующую математическую модель. Пусть Х1, Х2, ..., Хn – независимые случайные величины, которые принимают соответствующие выборочные значения (для данной выборки значения х1, х2, ..., хn) и пусть случайная величина 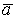 получена на основе случайных величин Х1, Х2, ..., Хn, то есть
получена на основе случайных величин Х1, Х2, ..., Хn, то есть 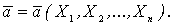 Будем считать, как и ранее, что случайные величины Х1, Х2, ..., Хn имеют один и тот же закон распределения с плотностью распределения величины Х (генеральной совокупности)f(x). Тогда
Будем считать, как и ранее, что случайные величины Х1, Х2, ..., Хn имеют один и тот же закон распределения с плотностью распределения величины Х (генеральной совокупности)f(x). Тогда 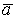 является случайной величиной, закон распределения которой зависит от n и от f(x). Для того чтобы оценка
является случайной величиной, закон распределения которой зависит от n и от f(x). Для того чтобы оценка 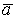 имела практическую ценность она должна обладать следующими свойствами.
имела практическую ценность она должна обладать следующими свойствами.
1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:
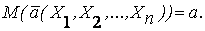
В противном случае оценка называется смещенной и допускает систематическую ошибку. Так, рассмотренное ранее среднее выборочное 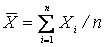 является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия
является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия 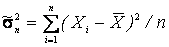 - является смещенной оценкой генеральной дисперсии.
- является смещенной оценкой генеральной дисперсии.
2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:
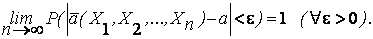
Это условие будет выполняться, если

и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.
3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:
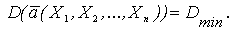
Такая оценка называется эффективной.
Заключение. При обработке экспериментальных данных необходимо руководствоваться сформулированными свойствами оценок.
В качестве примера покажем, что рассмотренные ранее оценки: выборочное среднее 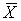 и выборочная дисперсия
и выборочная дисперсия 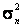 , будучи несмещенными, являются и состоятельными оценками. Действительно, так как согласно теореме Чебышева
, будучи несмещенными, являются и состоятельными оценками. Действительно, так как согласно теореме Чебышева
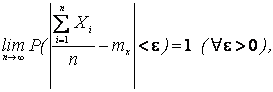
то выборочное среднее 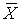 является состоятельной оценкой.
является состоятельной оценкой.
Для того чтобы доказать, что выборочная дисперсия 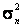 является состоятельной оценкой, покажем вначале, что смещенная оценка
является состоятельной оценкой, покажем вначале, что смещенная оценка 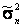 - состоятельная оценка. С этой целью запишем:
- состоятельная оценка. С этой целью запишем:
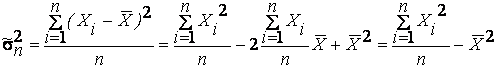 (8.1)
(8.1)
При n ® ¥ по вероятности случайная величина 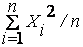 стремится к М(Х2), а выборочное среднее
стремится к М(Х2), а выборочное среднее 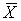 – к среднему генеральному mx. Тогда из соотношения (1) следует, что по вероятности
– к среднему генеральному mx. Тогда из соотношения (1) следует, что по вероятности 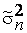 стремится при n ® ¥ к величине М(Х2)-mx2=D(X)=s2, которая является генеральной дисперсией. Тем самым доказана состоятельность оценки
стремится при n ® ¥ к величине М(Х2)-mx2=D(X)=s2, которая является генеральной дисперсией. Тем самым доказана состоятельность оценки 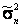 . Если теперь рассмотреть несмещенную оценку генеральной дисперсии
. Если теперь рассмотреть несмещенную оценку генеральной дисперсии 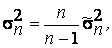 то поскольку множитель
то поскольку множитель 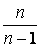 стремится к единице при n ® ¥, а
стремится к единице при n ® ¥, а 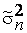 стремится по вероятности к
стремится по вероятности к 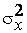 , то и оценка
, то и оценка 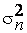 стремится по вероятности к
стремится по вероятности к 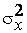 , что доказывает состоятельность оценки
, что доказывает состоятельность оценки 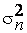 .
.
Замечание. Для простоты изложения формулы оценок математического ожидания и дисперсии, которые были использованы при доказательстве свойств оценок, были построены с использованием статистического ряда. Если данные выборки представлено в виде интервального вариационного ряда, то для вычисления соответствующих выборочных числовых характеристик используют следующие формулы.
1.Выборочное взвешенное среднее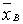 :
:
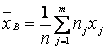 .
.
2. Выборочная взвешенная дисперсия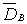 :
:
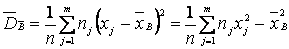 ,
,
которая является смещенной оценкой и несмещенная оценка
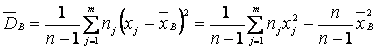 .
.
Здесь п – объем выборки, т – число разных вариант, nj – частоты вариант (п1+п2+…+пт=п).
6. Оценка неизвестных законов распределения.
Точечные оценки неизвестных параметров распределения. Свойства точечных оценок.
Оценки параметров распределения бывают точечные и интервальные.
Пусть 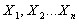 – выборка объема “n” (1)
– выборка объема “n” (1)
Функцию выборки (1) 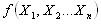 называют статистикой.
называют статистикой.
Предположим, что нужно оценить неизвестный параметр 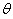 изучаемой случайной величины
изучаемой случайной величины 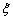 .
.
Def: Статистику 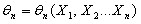 , значения которой близки к оцениваемому параметру
, значения которой близки к оцениваемому параметру 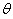 , называют точечной оценкой параметра
, называют точечной оценкой параметра 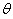 .
.
При 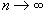 оценка
оценка 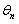 должна приближаться к параметру
должна приближаться к параметру 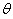 .
.
Оценка 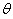 – случайная величина, поэтому мы не можем потребовать, чтобы оценка стремилась к
– случайная величина, поэтому мы не можем потребовать, чтобы оценка стремилась к 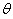 в обычном смысле.
в обычном смысле.
Def: Оценка 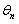 называется состоятельной, если при
называется состоятельной, если при 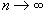
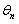 в вероятностном смысле стремится к
в вероятностном смысле стремится к 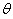 .
.
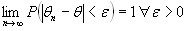 – обычная сходимость.
– обычная сходимость.
Поскольку оценка 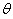 – случайная величина, то рассмотрим ее математическое ожидание
– случайная величина, то рассмотрим ее математическое ожидание
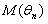 .
.
Def: Оценка 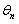 называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром
называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром 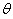 :
: 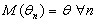 .
.
Несмещенная оценка с минимальной дисперсией называется эффективной.
Основные оцениваемые параметры распределения:
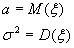
Построим точечные оценки для этих параметров.
Точечную оценку для “a” называют выборочное среднее.
Точечную оценку для 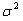 называют выборочная дисперсия.
называют выборочная дисперсия.
Выборочная средняя.
В качестве точечной оценки для “a” берут выборочную среднюю 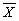 .
.
Def: выборочной средней 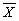 называется среднее арифметическое выборки.
называется среднее арифметическое выборки.
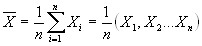 (2)
(2)
Теорема: выборочная средняя является состоятельной и несмещенной оценкой математического ожидания 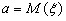 .
.
Доказательство.
Нужно доказать, что 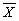 в вероятностном смысле стремится к “a”, и что
в вероятностном смысле стремится к “a”, и что 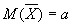 - несмещенность. Чтобы доказать это, к последовательности случайных величин
- несмещенность. Чтобы доказать это, к последовательности случайных величин 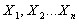 , каждая из которых имеет тот же закон распределения, что и
, каждая из которых имеет тот же закон распределения, что и 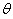 , применим теорему Чебышева:
, применим теорему Чебышева:
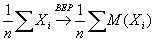 . В левой части – выборочная средняя.
. В левой части – выборочная средняя.
Найдем правую часть.
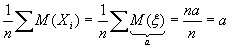
В силу теоремы Чебышева: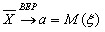
Самостоятельность доказана.
Вычислим математическое ожидание:
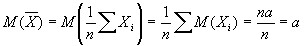
Теорема доказана.
Найдем дисперсию выборочной средней:
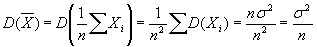
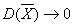 при
при 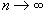
Из этого соотношения следует эффективность выборочной средней.
Таким образом, при больших значениях “n” имеем приближенное равенство:
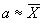 (оцениваемое значение “a” называют еще “генеральной средней”)
(оцениваемое значение “a” называют еще “генеральной средней”)
Выборочная дисперсия.
Выборочная дисперсия – точечная оценка для параметра 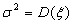 , который называют генеральной дисперсией.
, который называют генеральной дисперсией.
Def: выборочной дисперсией называют статистику 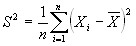 (3).
(3).
Для дискретной случайной величины:
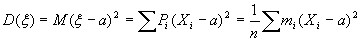 , где
, где 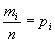
Докажем, что выборочная дисперсия 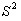 является состоятельной, но смещенной оценкой параметра
является состоятельной, но смещенной оценкой параметра 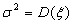 :
:
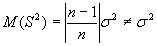
Получим вспомогательное утверждение (лемму):
Для любого 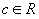 справедливо равенство
справедливо равенство 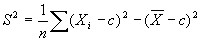 (4)
(4)
В (4) возьмем с = 0. Получим:
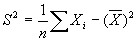 . Обозначим
. Обозначим 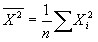 . Тогда:
. Тогда:
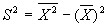 (3’).
(3’).
Доказательство.
Рассмотрим последовательность случайных величин:

Применим к ней теорему Чебышева:
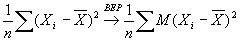 . В левой части –
. В левой части – 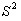 . Вычислим правую часть. Для этого воспользуемся (4):
. Вычислим правую часть. Для этого воспользуемся (4):
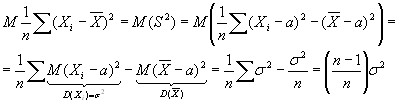
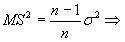 что выборочная дисперсия дает смещенную оценку. Вместе с тем, при
что выборочная дисперсия дает смещенную оценку. Вместе с тем, при 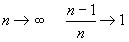 . Поэтому в силу теоремы Чебышева:
. Поэтому в силу теоремы Чебышева:
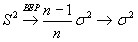 . Таким образом, выборочная дисперсия является состоятельной оценкой.
. Таким образом, выборочная дисперсия является состоятельной оценкой.
Исправленная выборочная дисперсия.
Получим несмещенную оценку для генеральной дисперсии 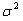 :
:
Def: Статистику 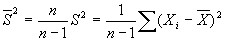 называют исправленной выборочной дисперсией.
называют исправленной выборочной дисперсией.
Очевидно, что 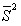 - несмещенная и состоятельная оценка для параметра
- несмещенная и состоятельная оценка для параметра 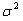 :
:
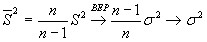
Проверим несмещенность:
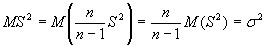
Замечание: так как при 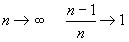 , то на практике для оценки
, то на практике для оценки 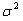 применяют (3’) ввиду ее удобства.
применяют (3’) ввиду ее удобства.
В качестве оценок для среднего квадратичного отклонения 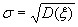 берут статистики
берут статистики 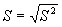 и
и 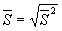 .Можно показать, что это – состоятельные оценки:
.Можно показать, что это – состоятельные оценки: 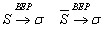
но обе оценки будут смещенными:
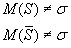
Интервальные оценки неизвестных.
1) Интервальная оценка и ее надежность.
Рассмотрим выборку 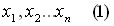 . Совокупность независимых случайных величин имеет тот же закон распределения, что и
. Совокупность независимых случайных величин имеет тот же закон распределения, что и 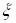 .
.
Пусть 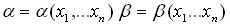 статистики такие, что всегда
статистики такие, что всегда 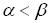 , тогда
, тогда 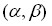 – случайный интервал.
– случайный интервал.
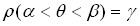
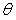 – оценка параметра.
– оценка параметра.
Def: если случайный интервал  может покрывать неизвестный параметр
может покрывать неизвестный параметр 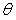 , то этот интервал называется интервальной оценкой для параметра
, то этот интервал называется интервальной оценкой для параметра 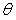 .
.
Пусть вероятность того, что параметр 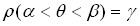 , тогда вероятность
, тогда вероятность 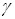 называется надежностью или доверительной вероятностью интервальной оценки
называется надежностью или доверительной вероятностью интервальной оценки 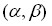 .
.
Понятие об интервальной оценке параметров.
При оценке вероятностных характеристик по ограниченному числу опытов могут быть допущены ошибки, т. е. отклонения этой оценки от истинного значения… Чтобы убедиться в том, что мы не допускаем чрезмерно грубой ошибки в оценке… Интервальной называют оценку, которая определяется двумя числами – концами интервала.Интервальная оценка математического ожидания.
Итак, Х ~ N(а,σ) (случайная величина Х имеет нормальное распределение с… При ~ эффективной оценкой параметра а является , при этом ~. Статистика имеет распределениеN(0; 1) независимо от…Интервальная оценка математического ожидания
При неизвестной диcперсии
Итак, Х ~ N(а,σ), причем числовые значения ни а, ни σ2 не известны. По случайной выборке найдем эффективную оценку параметра а: и… параметра σ2.Интервальная оценка генеральной дисперсии и среднего квадратического отклонения.
9.1. Интервальная оценка дисперсии (среднего квадратичного отклонения) при известном математическом ожидании Эффективной оценкой дисперсии в этом случае являетсяИнтервальная оценка дисперсии (среднего квадратичного отклонения) при неизвестном математическом ожидании
Наилучшей точечной оценкой дисперсии в этом случае является , и построение интервальной оценки для σ2 основано на статистике , которая при случайной выборке из генеральной…Интервальное оценивание генеральной доли
Для определения вероятностей интересующих нас событий мы применяем выборочный метод: проводим nнезависимых экспериментов, в каждом из которых может… В силу следствия из центральной предельной теоремы (теорема Муавра-Лапласа)… Поэтому при n>30доверительный интервал для генеральной доли можно построить, используя формулы (5.2)–(5.4):– Конец работы –
Используемые теги: Понятие, статистической, оценке, параметров0.073
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Понятие о статистической оценке параметров
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов